Draw a liner pair of angles. Bisect each of the two angles. Verify that the two bisecting rays are perpendicular to each other.
To solve the problem of drawing a linear pair of angles, bisecting each of the two angles, and verifying that the two bisecting rays are perpendicular to each other, follow these steps:
1. Draw a Line Segment:
- Start by drawing a straight line segment AB. This will serve as the base for your angles.
Hint: Use a ruler to ensure the line is straight.
2. Create a 90-degree Angle:
- At point A, use a compass to draw an arc above and below the line segment AB.
- Without changing the compass width, place the compass at point B and draw two arcs that intersect the previous arcs.
- Label the intersection points as C and D.
- Draw a line segment connecting points C and D. This line is perpendicular to AB and creates two angles of 90 degrees at point A.
Hint: Ensure the compass width is consistent when drawing arcs from both points.
3. Label the Angles:
- The two angles formed at point A are both 90 degrees. Label these angles as angle X and angle Y.
Hint: Clearly label the angles to avoid confusion later.
4. Bisect Each Angle:
- To bisect angle X (90 degrees), place the compass at point A and draw an arc that intersects both rays of angle X. Label the intersection points as E and F.
- Without changing the compass width, draw arcs from points E and F. Label the intersection of these arcs as G. Draw a line segment from point A to point G. This line bisects angle X into two angles of 45 degrees each.
- Repeat the same process for angle Y to find its bisector, labeling the intersection point as H. Draw a line segment from point A to point H.
Hint: Make sure to take more than half the distance when drawing arcs for accurate bisectors.
5. Verify the Bisectors are Perpendicular:
- Now, you have two bisecting rays AG and AH. Since both angles X and Y were originally 90 degrees, each bisector creates two angles of 45 degrees.
- The angles formed between the two bisectors AG and AH at point A are 90 degrees, confirming that the two bisecting rays are perpendicular to each other.
Hint: Use a protractor to measure the angles if necessary to verify they are indeed 90 degrees.
Final Verification:
- You can conclude that the two bisecting rays AG and AH are perpendicular to each other as they form a right angle at point A.
- Start by drawing a straight line segment AB. This will serve as the base for your angles.
- At point A, use a compass to draw an arc above and below the line segment AB.
- Without changing the compass width, place the compass at point B and draw two arcs that intersect the previous arcs.
- Label the intersection points as C and D.
- Draw a line segment connecting points C and D. This line is perpendicular to AB and creates two angles of 90 degrees at point A.
- The two angles formed at point A are both 90 degrees. Label these angles as angle X and angle Y.
- To bisect angle X (90 degrees), place the compass at point A and draw an arc that intersects both rays of angle X. Label the intersection points as E and F.
- Without changing the compass width, draw arcs from points E and F. Label the intersection of these arcs as G. Draw a line segment from point A to point G. This line bisects angle X into two angles of 45 degrees each.
- Repeat the same process for angle Y to find its bisector, labeling the intersection point as H. Draw a line segment from point A to point H.
- Now, you have two bisecting rays AG and AH. Since both angles X and Y were originally 90 degrees, each bisector creates two angles of 45 degrees.
- The angles formed between the two bisectors AG and AH at point A are 90 degrees, confirming that the two bisecting rays are perpendicular to each other.
- You can conclude that the two bisecting rays AG and AH are perpendicular to each other as they form a right angle at point A.
Topper's Solved these Questions
Similar Questions
The diagonals of a ||gm bisect each other
View SolutionWhich of the following statements are true for a rectangle? It has two pairs of equal sides. It has all its sides of equal length. Its diagonals are equal. Its diagonals bisect each other. Its diagonals are perpendicular. Its diagonals are perpendicular and bisect each other. Its diagonals are equal and bisect each other. Its diagonals are equal and perpendicular, and bisect each other. All rectangles are squares. All rhombuses are parallelograms. All squares are rhombuses and also rectangles. All squares are not parallelograms. A rectangle is a parallelogram with one of its angles equal to right angles.
View Solution
Knowledge Check
The diagonals of a rhombus bisect each other at _____ angles.
AAcuteBObtuseCRight.DStraight
If a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionTwo straight lines are cut by a transversal. If the bisectors of a pair of co-interior angles are perpendicular to each other , prove the two straight lines are parallel to each other.
View SolutionProve that, if a diameter of a circle bisects two chords of the circle then those two chords are parallel to each other.
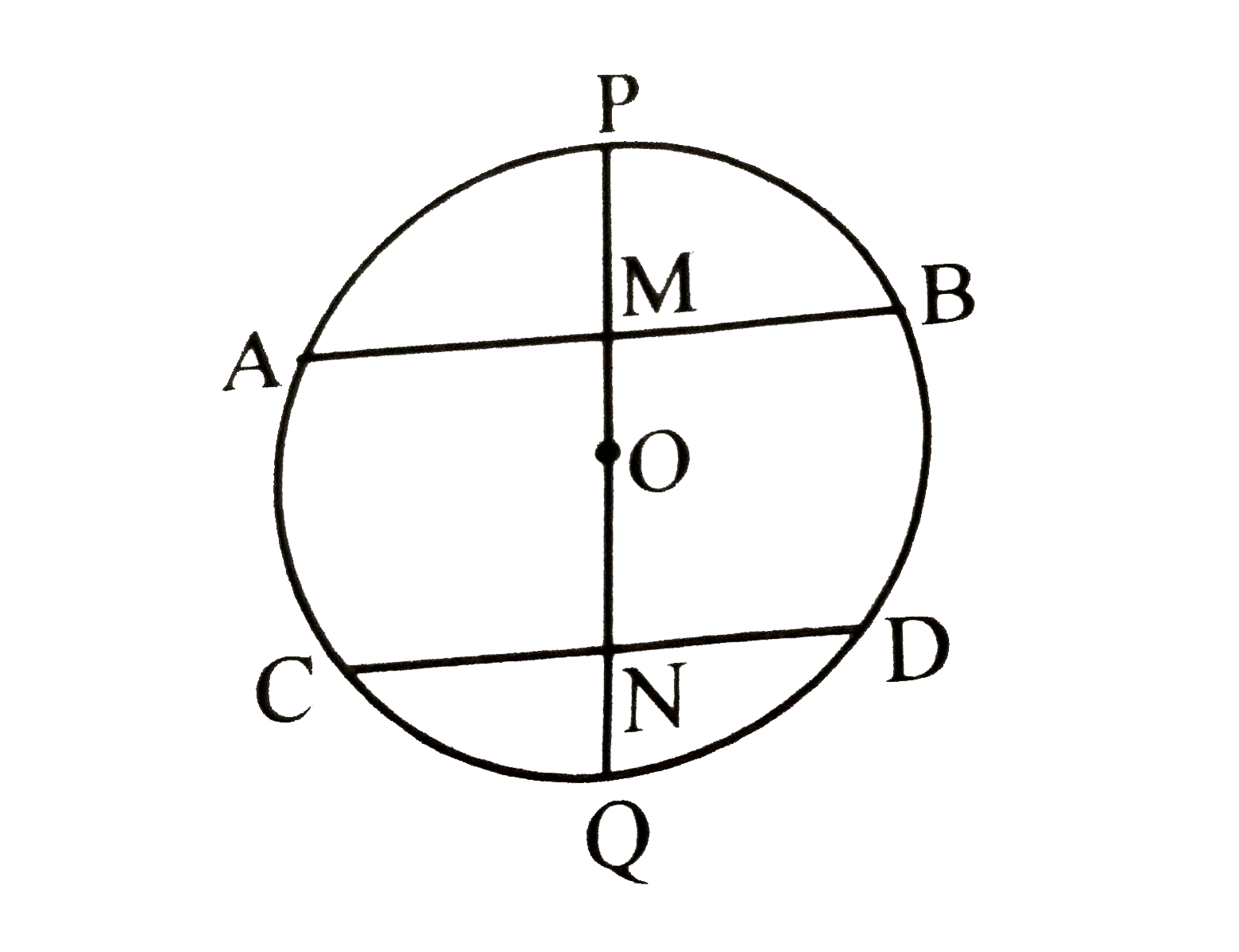
View SolutionIf diagonal of a quadrilateral bisects each other at right angles then it is a
View SolutionShow that the diagonals of a rhombus bisect each other at right angles.
View SolutionName the quadrilaterals whose diagonals (i) bisect each other (ii) are perpendicular bisectors of each other (iii) are equal
View SolutionWhich of the following statements are true for a rhombus?
View Solution
