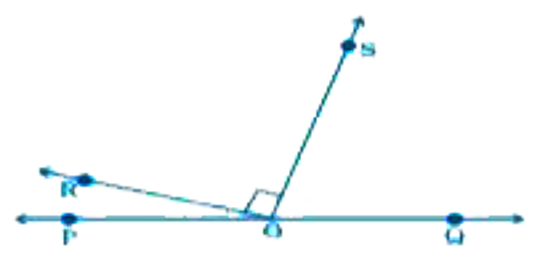
In Fig.6, ∠POQ≅∠ROS, can we say that ∠POR≅∠QOS
To determine whether ∠POR is congruent to ∠QOS given that ∠POQ≅∠ROS, we can follow these steps:
1. Identify the Given Information:
- We know that ∠POQ≅∠ROS. This means that these two angles are equal in measure.
2. Label the Angles:
- Let's denote:
- ∠POQ=θ3
- ∠ROS=θ1
- ∠POR=θ2
- From the given information, we have θ3=θ1.
3. Express ∠POR:
- The angle ∠POR can be expressed as the sum of two angles:
∠POR=∠POQ+∠QOR
- Therefore, we can write:
∠POR=θ3+∠QOR
4. Substitute θ3:
- Since θ3=θ1, we can substitute this into the equation:
∠POR=θ1+∠QOR
5. Express ∠QOS:
- The angle ∠QOS can also be expressed as:
∠QOS=∠ROS+∠QOR
- Substituting ∠ROS with θ1:
∠QOS=θ1+∠QOR
6. Compare ∠POR and ∠QOS:
- We now have:
∠POR=θ1+∠QOR
∠QOS=θ1+∠QOR
- Since both expressions are equal, we conclude that:
∠POR=∠QOS
7. Conclusion:
- Therefore, since ∠POR is equal to ∠QOS, we can say that:
∠POR≅∠QOS
Final Answer:
Yes, ∠POR≅∠QOS.
---
- We know that ∠POQ≅∠ROS. This means that these two angles are equal in measure.
- Let's denote:
- ∠POQ=θ3
- ∠ROS=θ1
- ∠POR=θ2
- From the given information, we have θ3=θ1.
- The angle ∠POR can be expressed as the sum of two angles:
∠POR=∠POQ+∠QOR
- Therefore, we can write:
∠POR=θ3+∠QOR
- Since θ3=θ1, we can substitute this into the equation:
∠POR=θ1+∠QOR
- The angle ∠QOS can also be expressed as:
∠QOS=∠ROS+∠QOR
- Substituting ∠ROS with θ1:
∠QOS=θ1+∠QOR
- We now have:
∠POR=θ1+∠QOR
∠QOS=θ1+∠QOR
- Since both expressions are equal, we conclude that:
∠POR=∠QOS
- Therefore, since ∠POR is equal to ∠QOS, we can say that:
∠POR≅∠QOS
Yes, ∠POR≅∠QOS.
Topper's Solved these Questions
Similar Questions
Knowledge Check
From Question 29, we can say that
Athe average speed is 40km/hBthe average velocity is 40km/hCthe average speed is 80km/hDthe average velocity is 80km/h
How can we say that charge is quantised ?
View SolutionIn Fig. 5.19, ∠ROS is a right angle and ∠POR and ∠QOS are in the ratio 1 : 5. Then, ∠QOS measures
View Solution10 In Fig. 6.19, angled at and ll POR is at right triangle right angled os a Q and pk PO 6 cm and Ps s4em, find QS RS and OR. Fig. 6.19
View SolutionWhen can we say that an object is in motion?
View SolutionHow can we say that rights imply duties?
View SolutionHow can we say that rights imply one's own duty?
View SolutionIn Fig. 6.12, BA || ED and BC || EF. Show that ∠ABC=∠DEF (Hint: Produce DE to intersect BC at P (say)]
View Solution
