Question

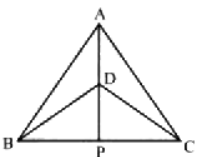
$ABCandDBC$
are both isosceles
triangles on a common base $BC$
such that $AandD$
lie on the same side of $BC\stackrel{.}{}$
Are triangles $ADB$
and $ADC$
congruent? Which condition
do you use? If $\angle BAC={40}^{0}and\angle BDC={100}^0;$
then find$\angle ADB$

Explanation

To solve the problem step by step, we will analyze the given information and use the properties of congruent triangles and isosceles triangles.

Step 1: Understand the Problem
We have two isosceles triangles, \( \triangle ABC \) and \( \triangle DBC \), sharing a common base \( BC \). Points \( A \) and \( D \) are on the same side of line \( BC \). We need to determine if triangles \( \triangle ADB \) and \( \triangle ADC \) are congruent and find the measure of angle \( ADB \).

Step 2: Identify Given Angles
We are given:
- \( \angle BAC = 40^\circ \)
- \( \angle BDC = 100^\circ \)

Step 3: Analyze the Isosceles Triangles
1. In triangle \( ABC \):
- Since it is isosceles, \( AB = AC \).
- The angles opposite these sides are equal: \( \angle ABC = \angle ACB \).

2. In triangle \( DBC \):
- Since it is isosceles, \( DB = DC \).
- The angles opposite these sides are equal: \( \angle DBC = \angle DCB \).

Step 4: Find Angles in Triangles
1. For triangle \( DBC \):
- The sum of angles in a triangle is \( 180^\circ \).
- Therefore, \( \angle DBC + \angle DCB + \angle BDC = 180^\circ \).
- Let \( \angle DBC = \angle DCB = x \).
- Thus, \( x + x + 100^\circ = 180^\circ \).
- This simplifies to \( 2x + 100^\circ = 180^\circ \).
- Solving for \( x \), we get \( 2x = 80^\circ \) so \( x = 40^\circ \).
- Therefore, \( \angle DBC = \angle DCB = 40^\circ \).

2. For triangle \( ABC \):
- Let \( \angle ABC = \angle ACB = y \).
- Thus, \( y + y + 40^\circ = 180^\circ \).
- This simplifies to \( 2y + 40^\circ = 180^\circ \).
- Solving for \( y \), we get \( 2y = 140^\circ \) so \( y = 70^\circ \).
- Therefore, \( \angle ABC = \angle ACB = 70^\circ \).

Step 5: Determine Congruence of Triangles
Now we check the triangles \( \triangle ADB \) and \( \triangle ADC \):
- We have:
- \( AB = AC \) (sides of isosceles triangle \( ABC \))
- \( DB = DC \) (sides of isosceles triangle \( DBC \))
- \( AD \) is common to both triangles.

Thus, by the Side-Side-Side (SSS) congruence criterion:
- \( AB = AC \)
- \( DB = DC \)
- \( AD = AD \)

Therefore, \( \triangle ADB \cong \triangle ADC \).

Step 6: Find Angle \( ADB \)
Since \( \triangle ADB \cong \triangle ADC \), the corresponding angles are equal:
- \( \angle ADB = \angle ADC \).

Now, we know:
- \( \angle ABC = 70^\circ \)
- \( \angle DBC = 40^\circ \)

Using the triangle sum property in triangle \( ADB \):
- \( \angle ADB + \angle ABD + \angle BAD = 180^\circ \)
- \( \angle ADB + 70^\circ + 20^\circ = 180^\circ \) (since \( \angle BAD = \angle BAC = 40^\circ \))
- Therefore, \( \angle ADB + 90^\circ = 180^\circ \)
- Thus, \( \angle ADB = 90^\circ \).

Final Answer
The angle \( \angle ADB = 90^\circ \).

---