Express cot200∘ in terms of θR.
To express cot200∘ in terms of the reference angle θR, we will follow these steps:
Step 1: Identify the Quadrant
The angle 200∘ lies in the third quadrant. Angles in the third quadrant range from 180∘ to 270∘.
Step 2: Find the Reference Angle
The reference angle θR for any angle in the third quadrant can be calculated using the formula:
θR=θ−180∘
where θ is the given angle.
Step 3: Calculate the Reference Angle
Substituting θ=200∘:
θR=200∘−180∘=20∘
Step 4: Express cot200∘ in Terms of θR
In the third quadrant, the cotangent function is positive. Therefore, we can express cot200∘ in terms of θR:
cot200∘=cot(180∘+θR)=cot(180∘+20∘)=cot20∘
Final Answer
Thus, we can express cot200∘ in terms of θR:
cot200∘=cot(20∘)
The angle 200∘ lies in the third quadrant. Angles in the third quadrant range from 180∘ to 270∘.
The reference angle θR for any angle in the third quadrant can be calculated using the formula:
θR=θ−180∘
where θ is the given angle.
Substituting θ=200∘:
θR=200∘−180∘=20∘
In the third quadrant, the cotangent function is positive. Therefore, we can express cot200∘ in terms of θR:
cot200∘=cot(180∘+θR)=cot(180∘+20∘)=cot20∘
Thus, we can express cot200∘ in terms of θR:
cot200∘=cot(20∘)
Topper's Solved these Questions
Similar Questions
Express cos130∘ in terms of θR.
View SolutionExpress sin320∘ in terms of θR.
View SolutionExpress cotA in terms of cos2A
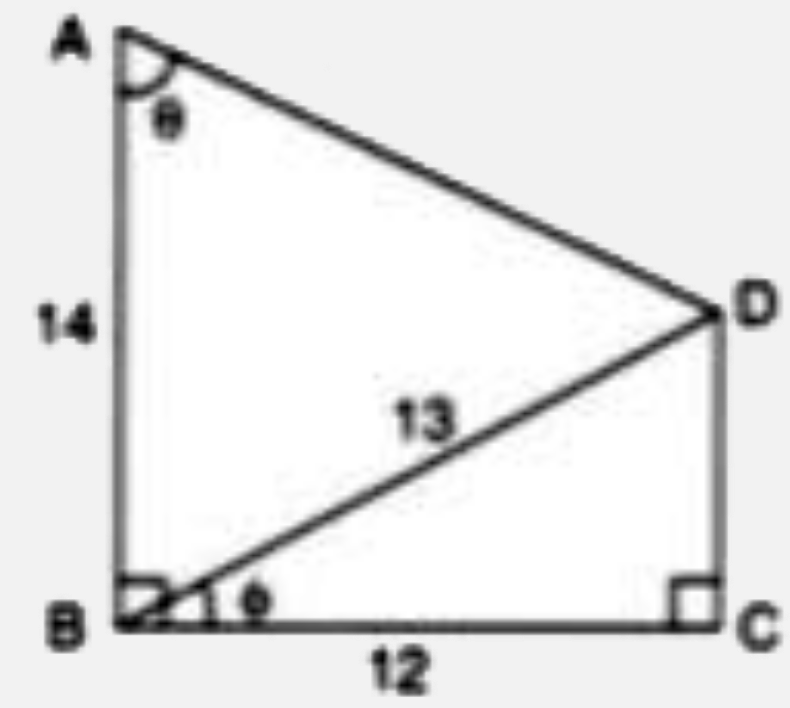
View SolutionUsing the measurements given in the following figure :
Write an expression for AD in terms of θ
 View Solution
View SolutionExpress cot85o+cos75oin terms of trigonometric ratios of angles between 0oand 45o
View SolutionExpress cos75⊕cot75o in terms of angles between 0o and 30o .
View SolutionIf sinθ=aandsin2θ=b, find an expression for cosθ in terms of a and b. Hence find a relation between a and b not involving θ.
View SolutionExpress the following in terms of angles between 0∘ and 45∘
cosec68∘+cot72∘View SolutionThe value of cot−1(−x)x∈R in terms of cot−1x is ……..
View SolutionThe value of cot−1(−x)x∈R in terms of cot−1x is
View Solution

