Ram is preparing for IIT JEE. He sets on to tackle a typical problem in mechanics. He sees that the wedge is kept on a smooth ground and it's inclined surface is also smooth. A block is projected on it as shown. Both the block and wedge have equal mass. Can you help him find the answer to following three question?
 What is the radius of curvature of it's path at the highest point?
What is the radius of curvature of it's path at the highest point?
0
v20cos2θg(sinθcosθ+sin2θ)
v20cos2θ2g(1+sin2θ)
None of these
The correct Answer is:D
v20cos2θ(1+sin2θ)8gsin2θ
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Multiple objective
131 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Knowledge Check
Ram is preparing for IIT JEE. He sets on to tackle a typical problem in mechanics. He sees that the wedge is kept on a smooth ground and it's inclined surface is also smooth. A block is projected on it as shown. Both the block and wedge have equal mass. Can you help him find the answer to following three question?
 How does the path of block look like as seen from ground.A
How does the path of block look like as seen from ground.A B
B C
C D
D
Ram is preparing for IIT JEE. He sets on to tackle a typical problem in mechanics. He sees that the wedge is kept on a smooth ground and it's inclined surface is also smooth. A block is projected on it as shown. Both the block and wedge have equal mass. Can you help him find the answer to following three question?
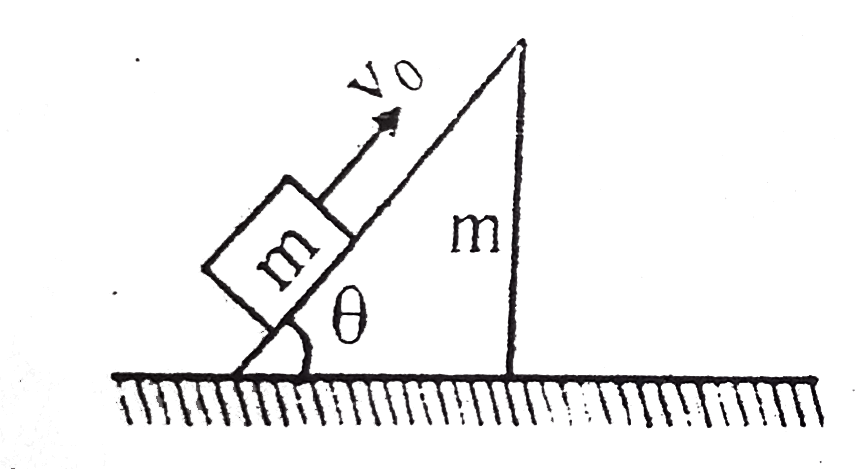 He sets on to find the maximum height attained by the block, assuming the block does not fall off to the other side. Which of the following equation is correct.Amgh=12mv20 (by conservation of energy) where h is maximum height of the block.B02=v20−2gsinθ×s where is maximum displacement along the inclined surfaceCmv0=mv+mv (by conservation of momentum) and 12mv20=12mv2+12mv2+mghDNone of these
He sets on to find the maximum height attained by the block, assuming the block does not fall off to the other side. Which of the following equation is correct.Amgh=12mv20 (by conservation of energy) where h is maximum height of the block.B02=v20−2gsinθ×s where is maximum displacement along the inclined surfaceCmv0=mv+mv (by conservation of momentum) and 12mv20=12mv2+12mv2+mghDNone of theseA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest
 A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the above
A(a) the position of the centre of mass of the system will changeB(b) the position of centre of mass of the system will change along the vertical but not along the horizontalC(c) the total energy of the system will remain constantD(d) All of the above
A smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?

View SolutionA smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?

View SolutionA smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?

View SolutionA block of mass m rests on a stationary wedge of mass M. The wedge can slide freely on a smooth horizontal surface as shown in figure. If the block starts from rest

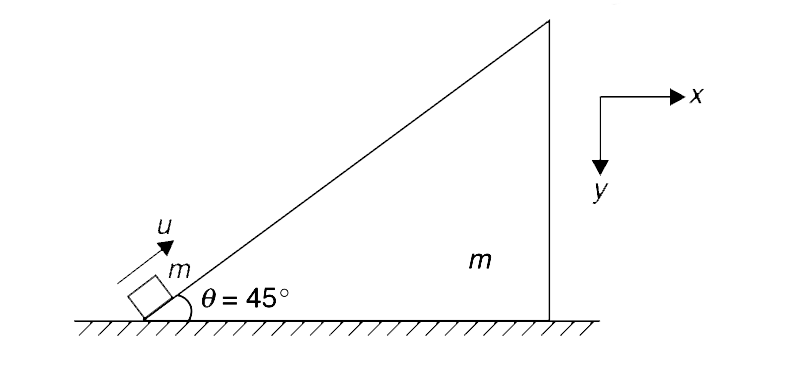
View SolutionA wedge of mass m is kept on a smooth table and its inclined surface is also smooth. A small block of mass m is projected from the bottom along the incline surface with velocity u. Assume that the block remains on the incline and take θ=45∘,g=10m/s2.
(a) Find the acceleration of the wedge and the x and y components of acceleration of the block.
(b) Draw the approximate path of the block as observed by an observer on the ground. At what angle does the block hit the table?
(c) Calculate the radius of curvature of the path of the block when it is at the highest point.
View Solution


 .
.