A block of mass 1 kg kept on a rough horizontal surface (μ=0.4) is attached to a light spring (force constant =200N//m) whose other end is attached to a verticle wall. The block is pushed to compress the spring by a distance d and released. Find the value(s) of 'd' for which (spring + block) system loses its entire mechanical energy in form of heat.
4 cm
6 cm
8 cm
10 cm
The correct Answer is:A, C
The system will lose its entire mechanical energy if the block finally comes to rest at the mean position. Now suppose the block comes to rest for the first time after the start at a distance d1 from the mean position on the other side, then 12k(d2−d21)−μmg(d+d1)=0

(From work energy theorem, ΔK=0) Rightarrow d−d1=2μmgk⇒d1=d−2μmgk
Now, similarly if d2,d3 e.t.c. are the successive distances of the block from the mean position where it come to rest for the second, third times etc. then d2−d3=d1
−d2=d−d1=2μmgk⇒d2=d1−2μmgk=d−4μmgk
d3=d2−2μmgk=d−6μmgk
dn=d−2μmgk
we want dn=0
Rightarrow d=n(2μmgk)
i.e.d should be an integral multiple of 2μmgk
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Subjective
107 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A block of mass M is kept on a rough horizontal surface and is attached with massless spring of force constant k .The minimum constant force applied on the other end of the spring to lift the block is
View SolutionA block of mass m is kept on a rough horizontal surface and is attached with a massless spring of force constant k. The minimum constant force applied on the other end of the spring of lift the block is
View Solution
Knowledge Check
A block of mass 2kg is on a smooth horizontal surface. A light of force constant 800N/m has one end rigidly attached to a vertical wall and lying on that horizontal surface. Now the block is moved towards the wall compressing the spring over a distance f 5cm and then suddenly released. By the time the spring regains its natural length and looses contact with the block, the velocity acquired by the block will be
A200m/sB100m/sC2m/sD1m/sA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
 AmgπB2mgπC3mgπD4mgπ
AmgπB2mgπC3mgπD4mgπ
A block of mass M=1 kg resting on a smooth horizontal surface is connected to a horizontal light spring of spring constant k=6N/m whose other end is fixed to a verticall wall. Another block of mass m=0.5 kg is placed over the block M. If the coefficient of friction between the two blocks μ=0.4, find the maximum kinetic energy (in J) that the system can have for simple hormonic oscillation under the action of the spring.
View SolutionA block of mass M=1 kg resting on a smooth horizontal surface is connected to a horizontal light spring of spring constant k=6N/m whose other end is fixed to a verticall wall. Another block of mass m=0.5 kg is placed over the block M. If the coefficient of friction between the two blocks μ=0.4, find the maximum kinetic energy (in J) that the system can have for simple hormonic oscillation under the action of the spring.
View SolutionA block of mass 100g attached to a spring of stiffness 100N/m is lying on a frictionless floor as shown. The block is moved to compress the spring by 10cm and released. If the collision with the wall is elastic then find the time period of oscillations.

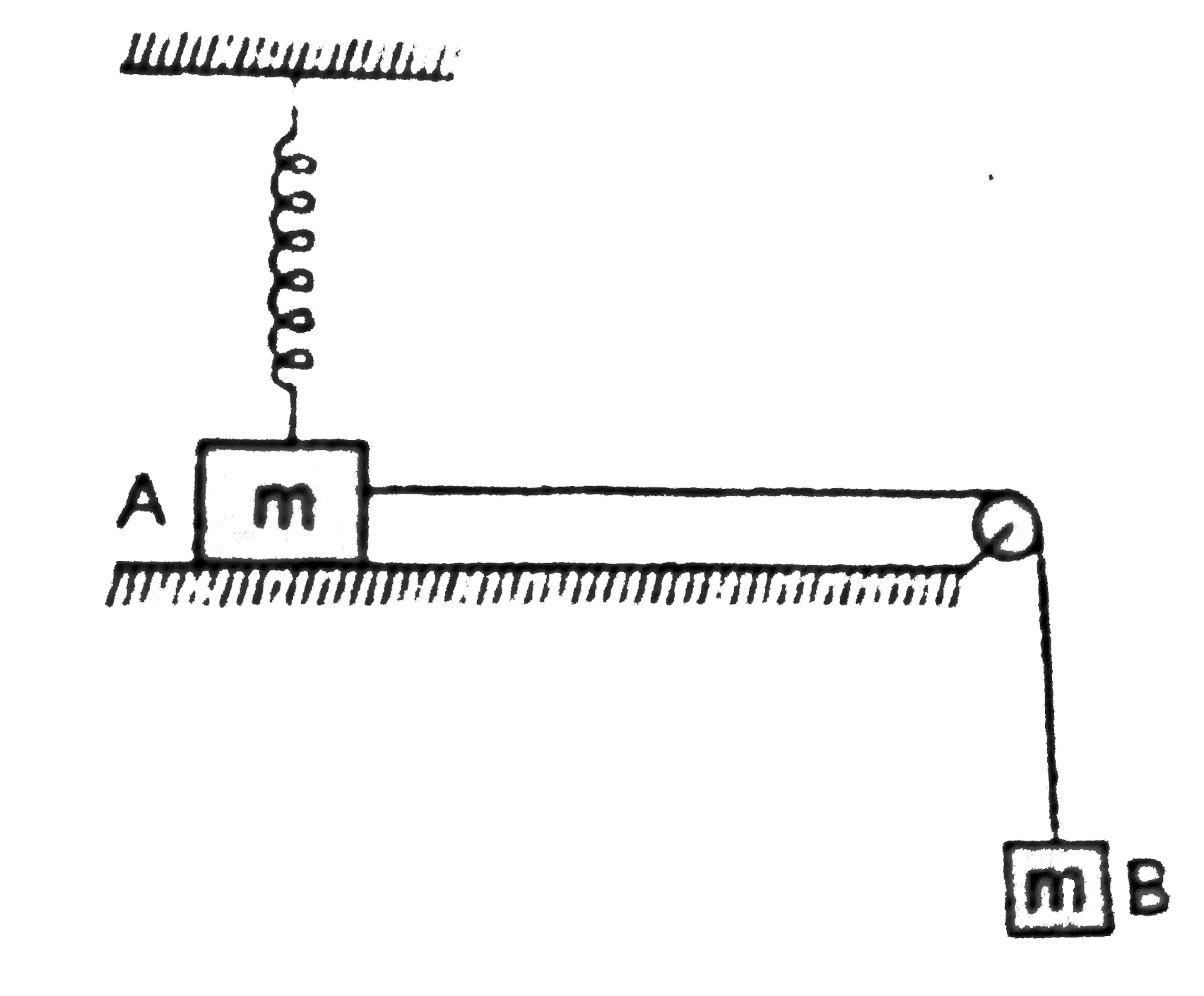
View SolutionFigure shows two block A and B, each having a mass of 320 g connected by a light string passing over a smooth light pulley. The horizontal surface on which the block A can slide is smooth. The block A is attached to spring constant 40N/m whose other end is fixed to a support 40 cm above the horizontal surface. Initially, the spring is vertical and unstretched when the system is released to move. Find the velocity of the block A at the instant it breaks off the surface below it. Take g=10m/s2 .
View SolutionFigure shown a block P of mass m resting on a smooth horizontal surface, attached to a spring of force constant k which is rigidly fixed on the wall on left side, shown in the figure . At a distance l to the right of the block there is a rigid wall. If block is pushed towards left so that spring is compressed by a distance 5l/3 and when released, if will starts its oscillations. If collision of block with the wall is considered to be perfectly elastic. Find the time period of oscillation of the block.

View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is

View Solution
