Two blocks A and B of the same mass are connected to a light spring and placed on a smooth horizontal surface B is given velocity v0 (as shown in the figure) when the spring is in natural length. In the subsequent motion.
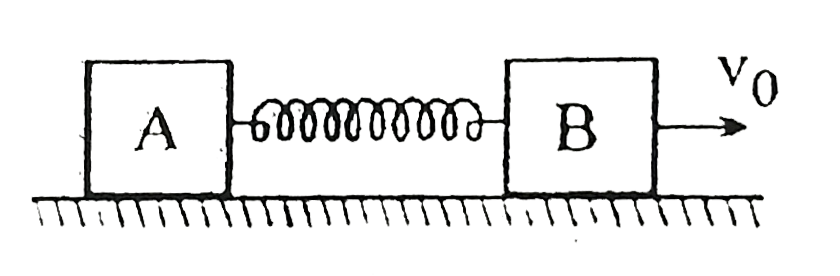
the maximum velocity of B will be v0
as seen from ground, A can move towards right only
the spring will have maximum extension when A and B both stop
the spring will be at natural length again when B is at rest
The correct Answer is:A, B, D
In CM frame the blocks will perform SHM as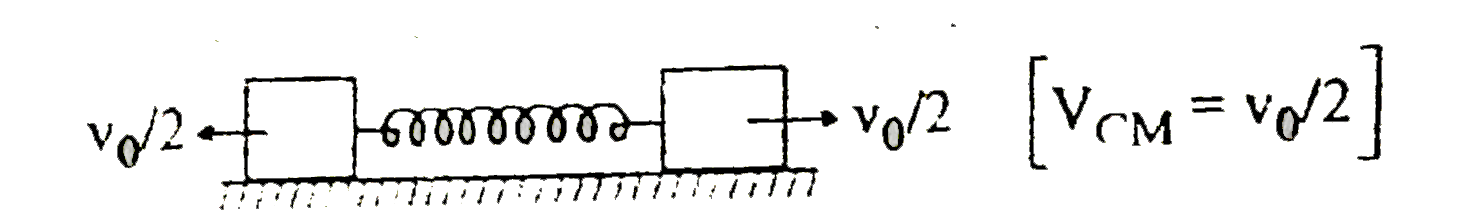 
[VCM=v0/2]
:.VCM is constant hence both will can have maximum velocity v0/2 towards right in CM frame.
:. (vB)max=v0 in ground frame
in CM frame (vA_(min)=−v0/2
:. (vA)min=0 in ground frame
i.e. A move only in right direction In CM frame vB=v0/2 left in the case when spring is at natural length
:.vB=0 in ground frame at that instant.
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Subjective
107 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
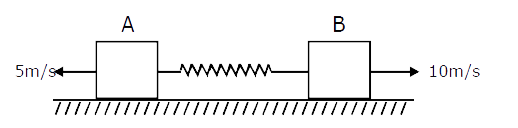
The two blocks A and B of same mass connected to a spring and placed on a smooth surface. They are given velocities (as shown in the figure) when the spring is in its natural length :
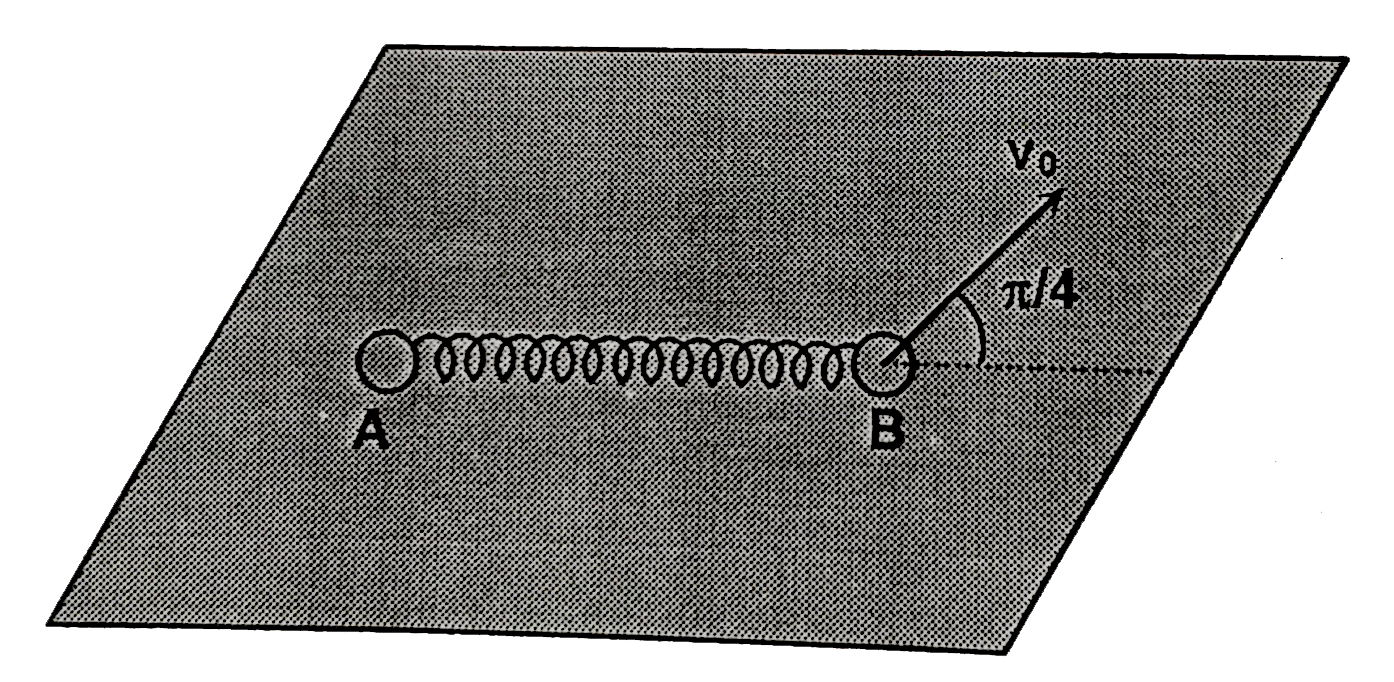
View SolutionA dumbbell consists of two balls A and B of mass m=1 kg and connected by a spring. The whole system is placed on a smooth horizontal surface as shown in the figure. Initially the spring is at its natural length, the ball B is imparted a velocity v0=8√7m/s in the direction shown. The spring constant of the spring is adjusted so that the length of the spring at maximum elongation is twice that of the natural, length of the spring. Find the maximum potential energy stored (in Joule) in the spring during the motion.
View Solution
Knowledge Check
Two masses A and B of mass M and 2M respectively are connected by a compressed ideal spring. The system in placed on a horizontal frictionless table and given a velocity uˆk in the z-direction as shown in the figure. The spring is then released. In the subsequent motion the line from B to A alwyas points along the ˆi unit vector. All some instant of time mass B has a x-component of velocity as vxˆi. The velocity →vA of mass A at that instant is :-
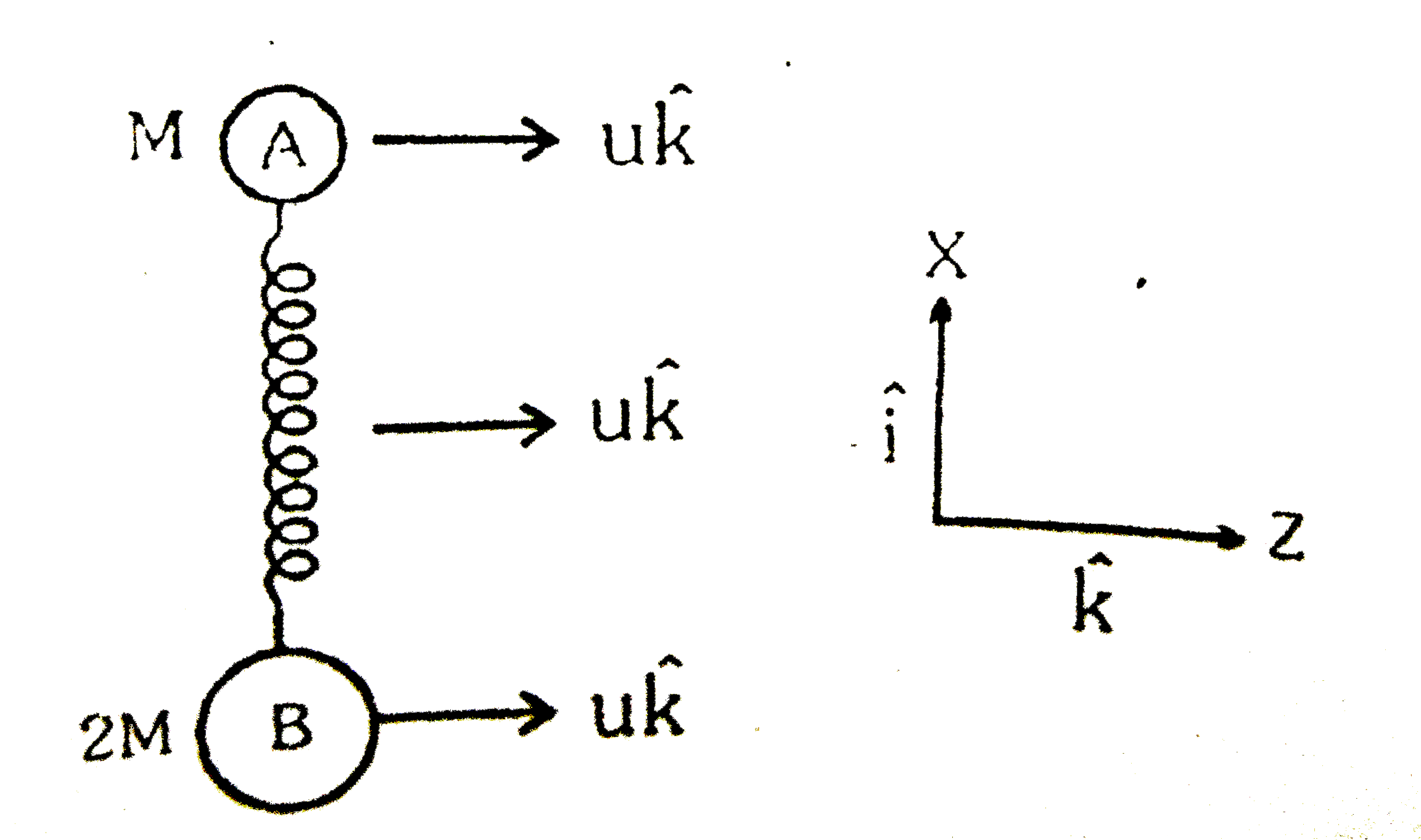Avxˆi+uˆkB−vxˆi+uˆkC−2vxˆi+uˆkD2vxˆi+uˆk
Two blocks A and B of masses m and 2m respectively are connected together by a light spring of stiffness k and then placed on a smooth horizontal surface. The blocks are pushed towards each other such that spring gets compressed by a length x0 and then released from rest. Find the work done on the block A by the spring, by the time the spring acquires its natural length.
View SolutionTwo blocks A and B of masses m & 2m placed on smooth horizontal surface are connected with a light spring. The two blocks are given velocities as shown when spring is at natural length.
(i) Find velocity of centre of mass (b) maximum extension in the spring
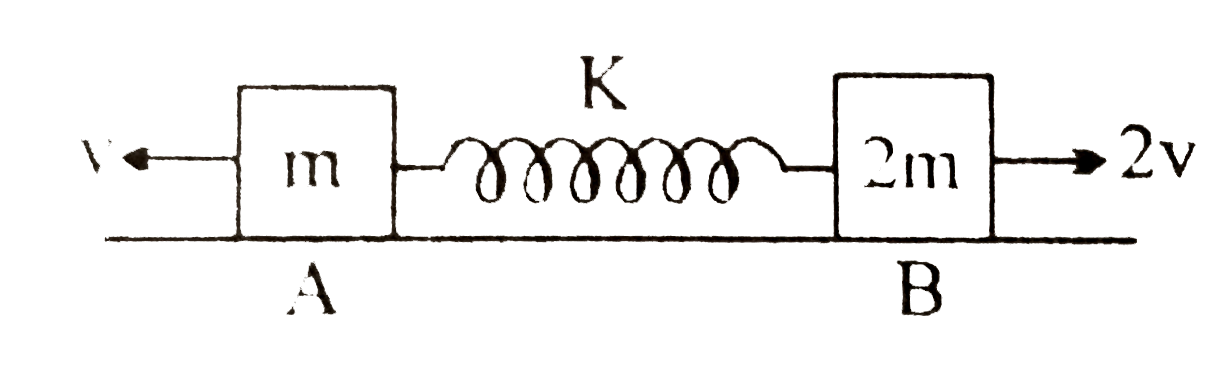
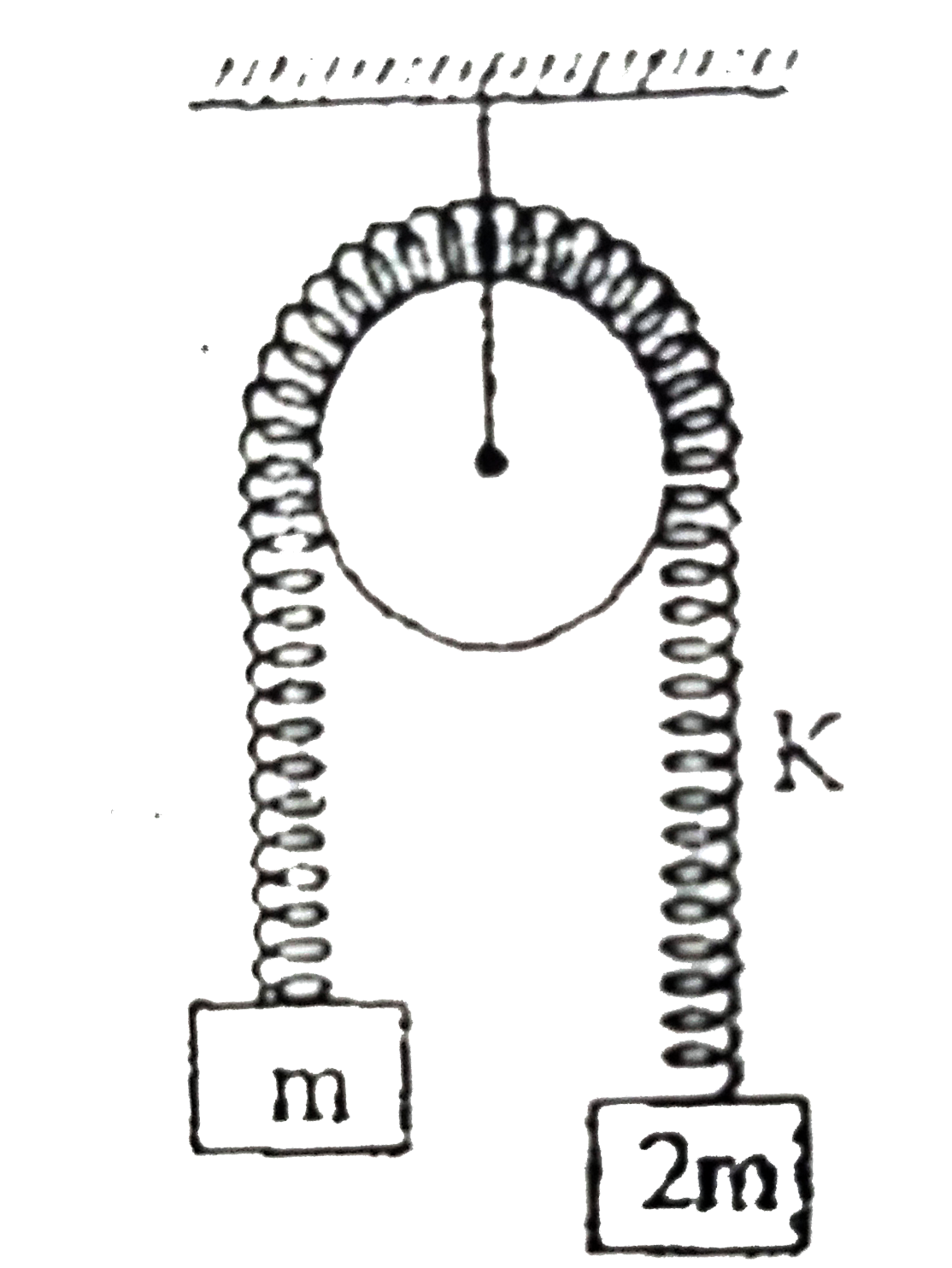
View SolutionTwo blocks of mass m and 2m are connected to a spring and wrapped around a smooth pulley as shown in the figure. Blocks are released together with spring in natural length. Calculate the maximum elongation (in meter) of the spring. Given mgK=3 meter.
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length
View SolutionTwo blocks A and B each of mass m are connected by a light spring of natural length L and spring constant k. The blocks are initially resting on a smooth horizontal floor with the spring at its natural length, as shown. A third identical block C, also of mass m, moves on the floor with a speed v along the line joining A to B and collides with A. Collision is elastic and head on. Then -
View SolutionTwo masses are connected by a spring as shown in the figure. One of the masses was given velocity v = 2 k, as shown in figure where 'k' is the spring constant. Then maximum extension in the spring will be
View SolutionTwo blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
View Solution