In a solid sphere two small symmetrical cavities are created whose centres lie on a diameter AB of sphere on opposite sides of the centre.
The gravitational field at the centre of the sphere is zero
The gravitational potential at the centre remains unaffected if cavitiesare not present
A circle at which all points have same potential is in the plane of diameter AB
A circle at which all points have some potential is in the plane perpendicular to the diameter AB
The correct Answer is:A, D
Due to symmetric mass distribution about centre the gravitational about centre the gravitational field at this point is equal to zero. And equipotential surface is ⊥ r to the diameter AB
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Subjective107videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic70videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning75videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE10videos
FLUID MECHANICS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
Inside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength G of the gravitational field inside the cavity.
View SolutionTwo chords AB and AC of a circle subtends angles equal to 90∘and150∘, respectively at the centre. Find∠BAC, if AB and AC lie on the opposite sides of the centre.
View Solution
Knowledge Check
- Question 1 - Select One or More
There is a uniformly charged non-conducting solid sphere. A small spherical cavity is made inside it. Distance of the centre of cavity is x from the centre of sphere
AElectric field intensity inside the cavity is zero if x=0BElectric field intensity inside cavity is non-zero if x≠0CElectric field inside the cavity is always uniformDThe magnitude of electric field intensity inside the cavity is proportional to x. - Question 2 - Select One
There is a uniformly charged non-conducting solid sphere. A spherical cavity is made whose centre does not coincide with the centre of solid sphere. Electric field intensity inside the cavity is
Adirectly proportional to distance of the point from centre of cavityBdirectly proportional to the distance of the point from centre of sphereCuniformDnot predictable due to insufficient information - Question 3 - Select One
Inside a uniform sphere of density ρ there is a spherical cavity whose centre is at a distance l from the centre of the sphere. Find the strength of the gravitational field inside the cavity.
AE=−23πGρlBE=−43πGρlCE=−43π2GρlDE=−43πGρ2l2
Two chords AB and AC of a circle subtends angles equal to 90∘and150∘, respectively at the centre. Find∠BAC, if AB and AC lie on the opposite sides of the centre.
View SolutionA solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?
 View Solution
View SolutionA solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?
 View Solution
View SolutionFigure shows a spherical cavity inside a lead sphere. The surface of the cavity passes through the centre of the sphere and touches the right side of the sphere. The mass of the sphere before hollowing was M. With what gravitational force does the hollowed out lead sphere attract a particle of mass m that lies at a distance d from the centre of the lead sphere on the straight line connecting the centres of the spheres and of the cavity.
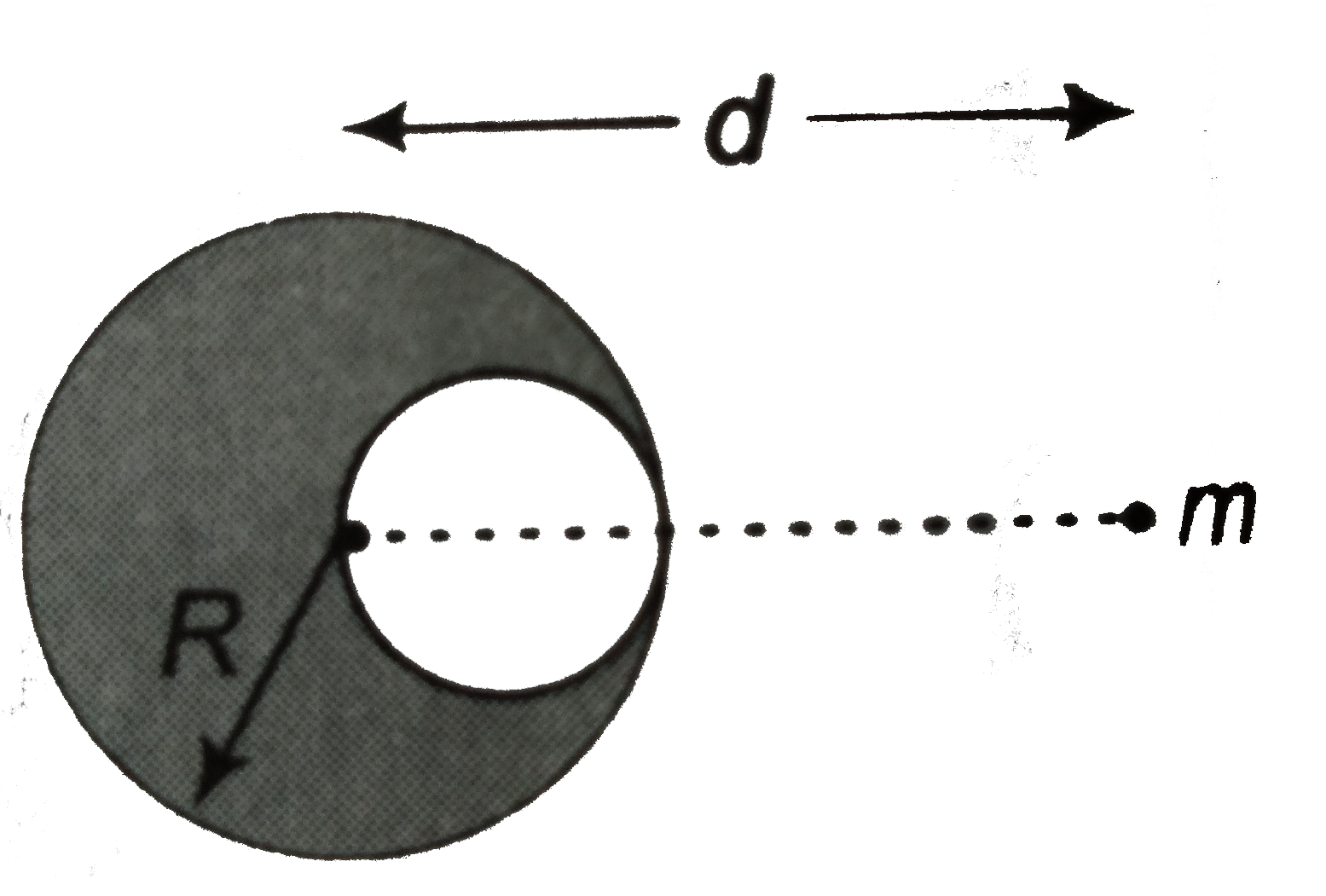 View Solution
View SolutionA solid sphere of radius R/2 is cut out of a solid sphere of radius R such that the spherical cavity so formed touches the surface on one side and the centre of the sphere on the other side, as shown. The initial mass of the solid sphere was M. If a particle of mass m is placed at a distance 2.5R from the centre of the cavity, then what is the gravitational attraction on the mass m?
 View Solution
View Solution

