Figure shows sqare current caarrying coil of edge lengthL. The magnetic field on the coil is given by →B=B0yLˆi+B0xLˆj where B0 is a positive constant.

If coil is free to rotate about x axis torque on the coil is given by 12iAB0ˆi
If coil is free to rotate about y-axis torque on coil is given by −12iAB0ˆj
Resultant force on coil is zero.
Equation for the torque →μ×→B where mu is magnetic moment of coil is not valid on the coil.
The correct Answer is:A, B, C, D
Wire segment(1)
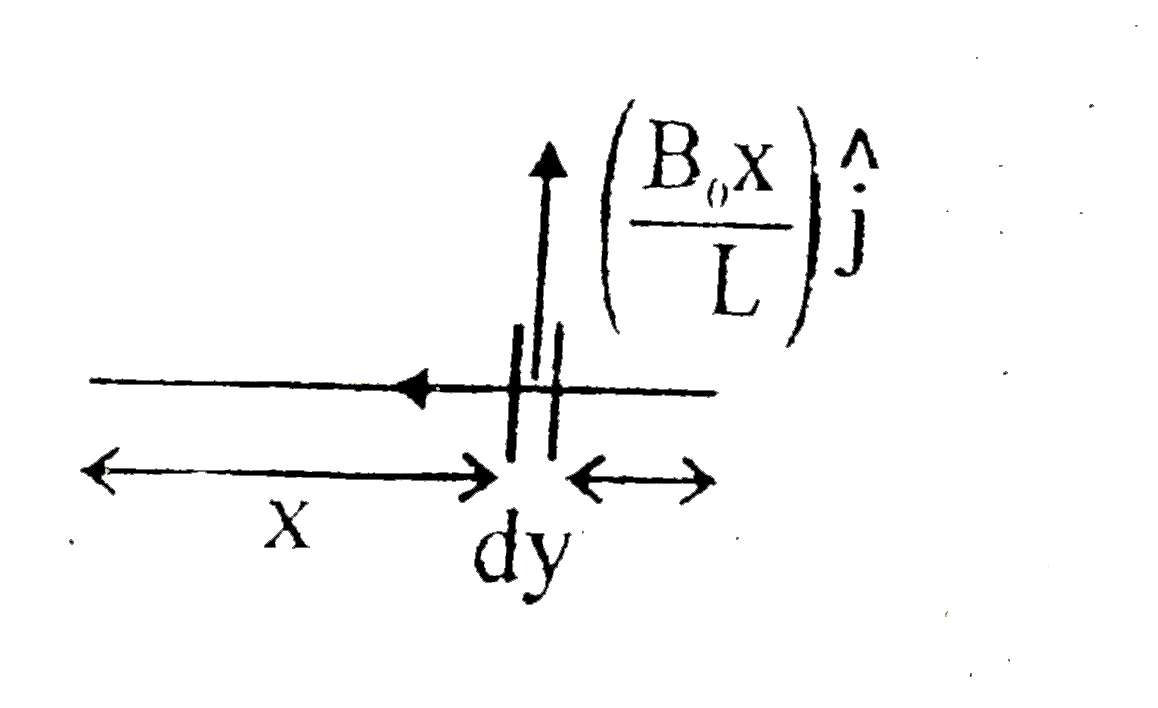
(d→f)=L∫0idx(B0x2)=iB0L2
d→f=−B0L2ˆk
Similary for →f2=−−iB0L2ˆk
→f3=iB0L2ˆk
→f4=iB0L2ˆk
→fn=0
If coil is constrained to rotate about
y−axis|→τ|=1(B0L2)L
=iAB02
Rightarrow Similarly for torque about torque has same magnitude
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Subjective
107 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A square of side L meters lies in the x−y plane in a region where tbe magnctic fleld is given by →B=B0(2ˆi+3ˆj+4ˆk) tesla _(3) where B0 is a constant. If the magnitude of flux passing through the square is yBaL2 weber, then find the value of y.
View SolutionA particle of charge q>0 is moving at speed v in the +z direction through a region of uniform magnetic field. The magnetic force on the particle →F=F0(3ˆi+4ˆj), where F0 is a positive constant.
(a) Determine the components Bx,By and Bz or at least as many of the three components as is possible from the information given.
(b) If it is given in addition that the magnetic field has magnitude 6F0qv , determine the magnitude of Bz.
View Solution
Knowledge Check
Figure shows a square loop carrying current I is present in the magnetic field which is given by →B=B0zLˆj+B0yLˆk where B0 is positive constant. Which of the following statement(s) is/are correct?
 Aforce on side (0,0) to (0,L) is (B0IL2)ˆiBforce on side (0,L) to (L,L) is −B0ILˆjCNet magnetic force on loop is zeroDforce on side (L,0) to (0,0) is zero
Aforce on side (0,0) to (0,L) is (B0IL2)ˆiBforce on side (0,L) to (L,L) is −B0ILˆjCNet magnetic force on loop is zeroDforce on side (L,0) to (0,0) is zeroA square of side L meters lies in the x-y plane in a region, where the magnetic field is give by B=B0(2ˆi+3ˆj+4ˆk)T, where B0 is constant. The magnitude of flux passing through the square is
A2B0L2WbB3B0L2WbC4B0L2WbD√29B0L2Wb
A particle of charge q>0 is moving at speed v in the +z direction through a region of uniform magnetic field. The magnetic force on the particle →F=F0(3ˆi+4ˆj), where F0 is a positive constant.
(a) Determine the components Bx,By and Bz or at least as many of the three components as is possible from the information given.
(b) If it is given in addition that the magnetic field has magnitude 6F0qv , determine the magnitude of Bz.
View SolutionThe figure shows a loop of wire carrying a current i as shown. There exists a uniform magnetic field along x-axis given by →B=B0ˆi. If the length of each side is a, then
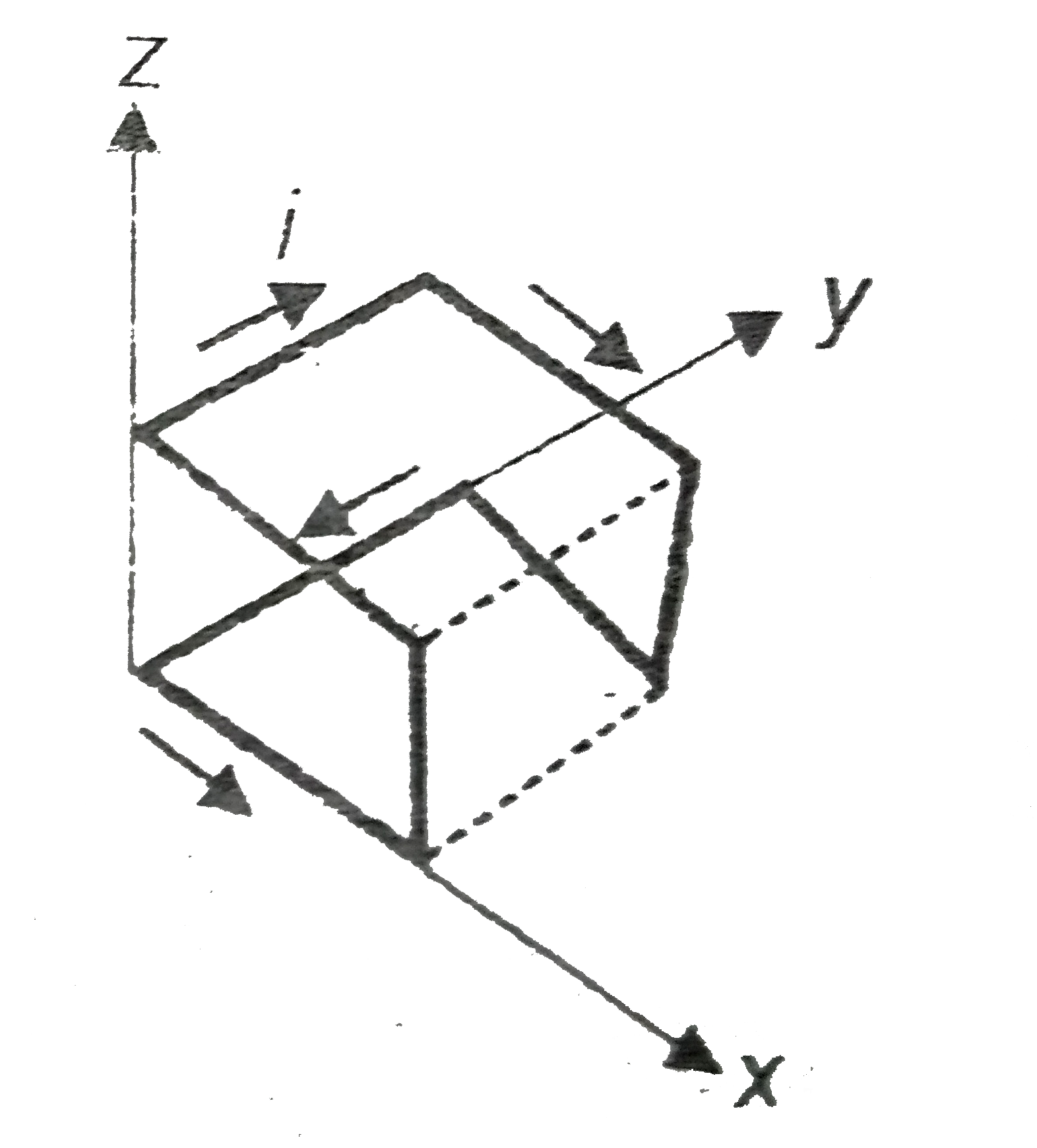
View SolutionThe figure shows a loop of wire carrying a current i as shown. There exists a uniform magnetic field along x-axis given by →B=B0ˆi. If the length of each side is a, then

View SolutionA square of side L meters lies in the x-y plane in a region, where the magnetic field is given by B=B0(2ˆi+3ˆj+4ˆk)T, where B0 is constant. The magnitude of flux passing through the square is
View SolutionA square of side L meters lies in the xy-plane in a region, where the magnetic field is given by =B0(2ˆi+3ˆj+4ˆk)T,, where B0 is constant. The magnitude of flux passing through the square is
View SolutionA square of side L meters lies in the x-y plane in a region, where the magnetic field is give by B=B0(2ˆi+3ˆj+4ˆk)T, where B0 is constant. The magnitude of flux passing through the square is
View Solution
