Initially springs are in natural length. An application of external varying force F causes the block to move slowly towards the wall, on smooth floor by a distance x.
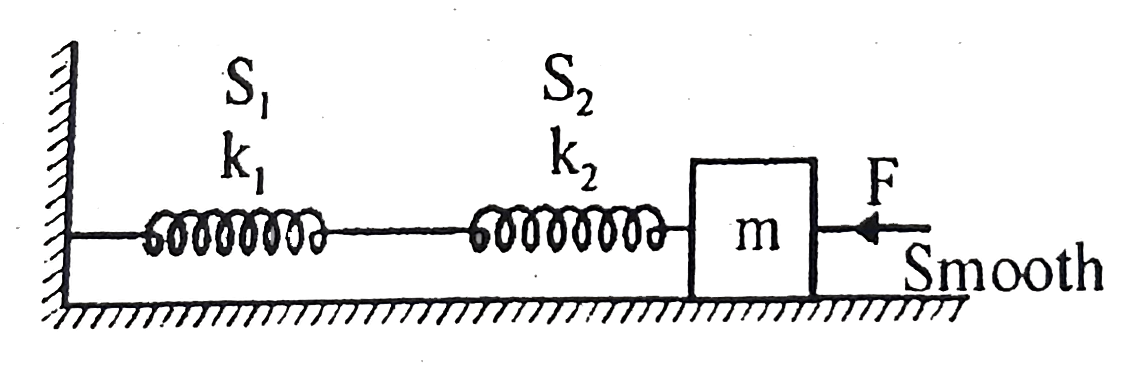
The correct Answer is:[(A)-Q(B)-S(C)-R(D)-P]
F1=k1x1∣F2=k2x2
k1x1=k2x2=kx
⇒x1=k2xk1+k2
&x1+x2=x
&x2=k1xk1+k2&k=k1k2k1+k2
(A) w.d. by S_(2) on block =−12kx2
(B) w.d. by S_(2) on S_(1) =12k1x21
(C) w.d. by 'F' on block =+12kx2
(D) w.d. by S_(1) on wall = zero (no disp. of pt. of application)
Topper's Solved these Questions
Similar Questions
Initially spring are in natural length An application of external varying force F causes the block to move slowly distance x towards wall on smooth floor:

Column - 1Column - 2(A)Work done by S2on block(P)zero(B)Work done by S2andS1(Q)−12(k1k2k1+k2)x2(C)Work done by F on block(R)12(k1k2k1+k2)x2(D)Work done by S1on wall(S)12k1k22x2(k1+k2)View SolutionTwo blocks having masses 8kg and 16kg are connected to the two ends of a light spring. The system is placed on a smooth horizontal floor. An inextensible string also connects B with ceiling as shown in the figure at the initial moment. Initially the spring has its natural length. A constant horizontal force F is applied to the heavier block as shown. What is the maximum possible value of F so the lighter block doesn't loose contact with ground?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 2kg is on a smooth horizontal surface. A light of force constant 800N/m has one end rigidly attached to a vertical wall and lying on that horizontal surface. Now the block is moved towards the wall compressing the spring over a distance f 5cm and then suddenly released. By the time the spring regains its natural length and looses contact with the block, the velocity acquired by the block will be
A200m/sB100m/sC2m/sD1m/s - Question 2 - Select One
Initially spring is in its natural length . The block of mass 3kg in contact with rigid wall . The block of mass 1kg is pushed through a distance 4cm towards the wall and then released. The velocity of the center of mass when the block of mass 3kg breaks off the wall is (k=100N/m)
 A0.1m/sB0.2m/sC0.3m/sD0.4m/s
A0.1m/sB0.2m/sC0.3m/sD0.4m/s
Two blocks having masses 8kg and 16 kg are connected to the two ends of a light spring. The system is placed on a smooth horizontal floor. An inextensible starting also connects B with ceiling as shown in figure at the initial moment. Initially the spring has its natural length. A constant horizontal force F is applied to the heavier block as shown. What is the maximum possible value of F so the lighter block doesn't loose contant with ground
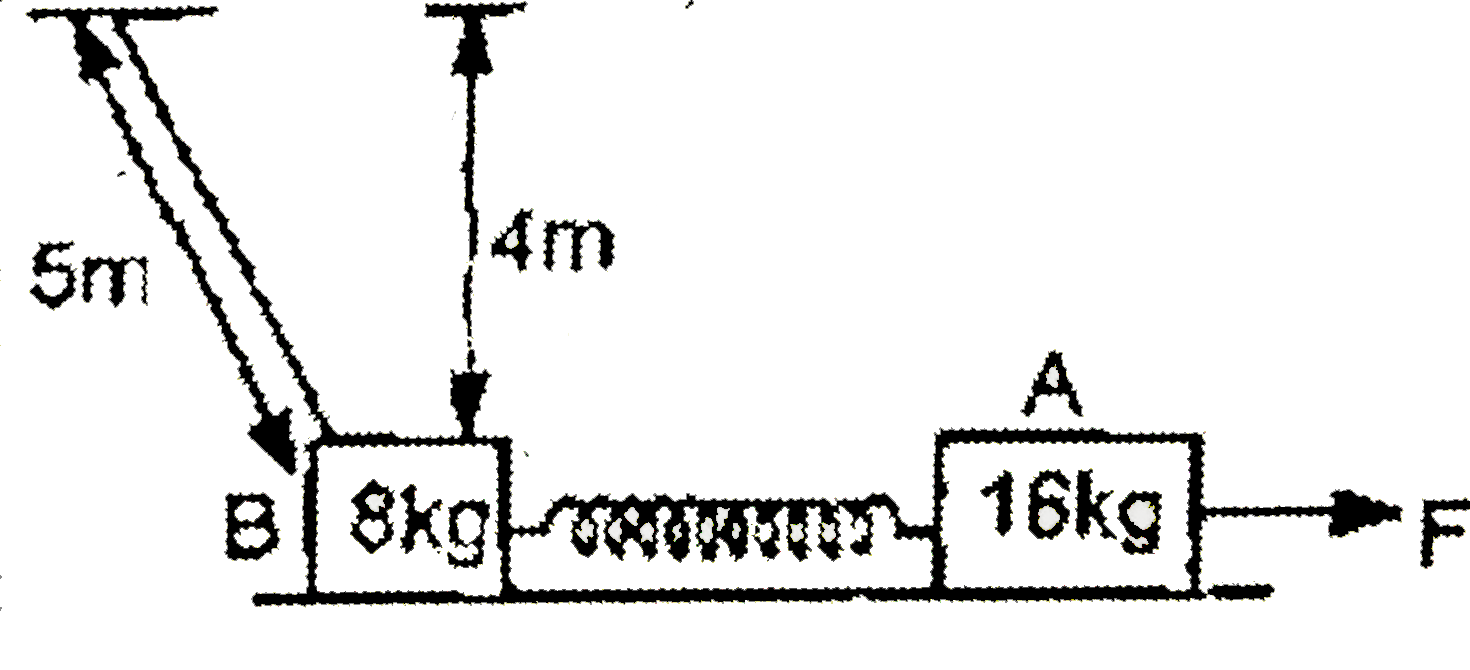 View Solution
View SolutionTwo blocks A and B, each of mass m, are connected by a spring of force constant K. Initially, the spring is in its natural length. A horizontal constant force F starts acting on block A at time t=0 and at time t , the extension in the spring is seen to be l. What is the displacement of the block A in time t ?
 View Solution
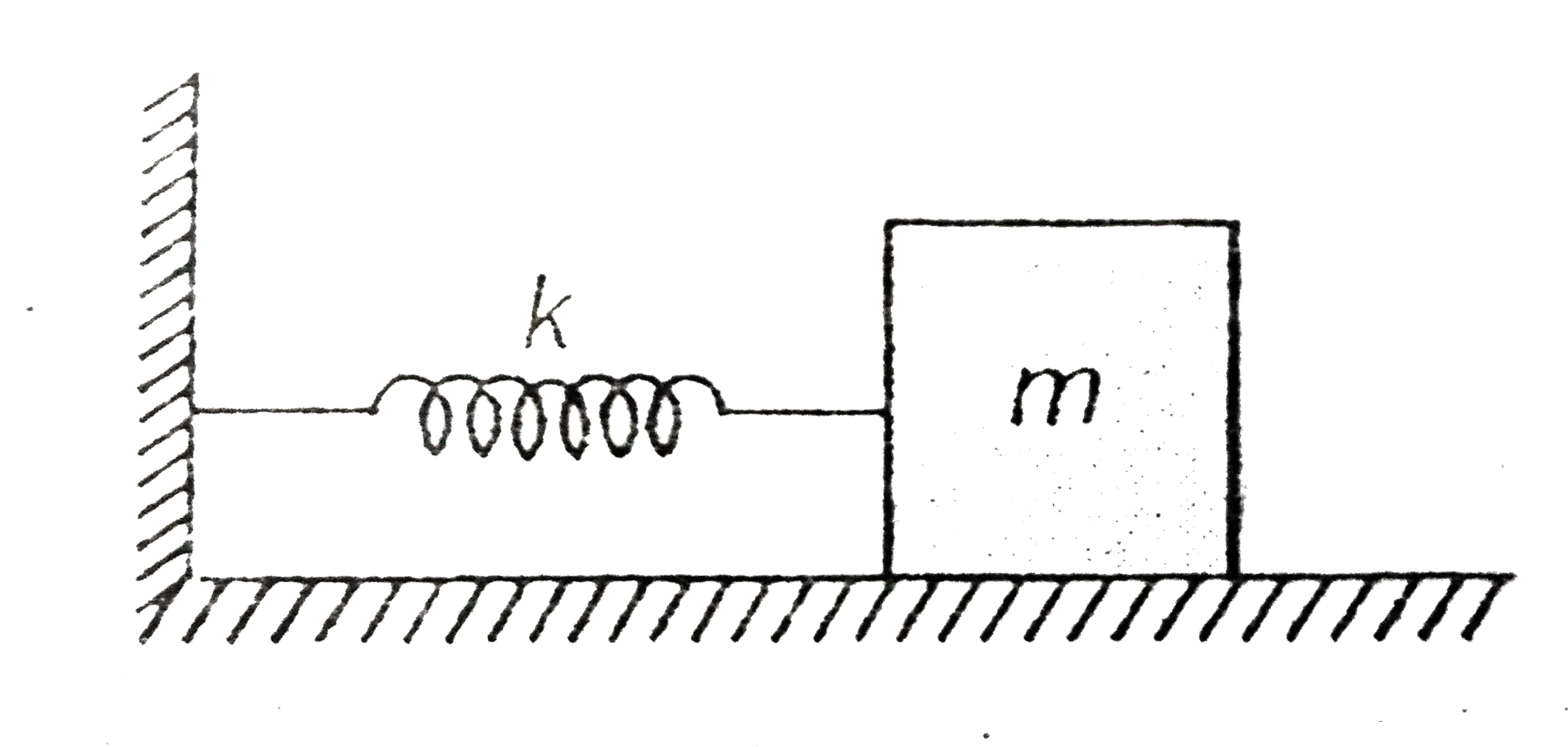
View SolutionFigure shows a block of mass 'm' resting on a smooth horizontal surface. It is connected to a rigid wall by a massless spring of stiffness 'k'. The spring is in its natural length. A constant horizontal force F starts acting on the block towards right. Find (i) speed of the block as it moves throught a distance x, (ii) speed when the block is in equlibrium and (iii) maximum extension produced in the speing.
 View Solution
View SolutionFigure shows a block of mass 'm' resting on a smooth horizontal surface. It is connected to a rigid wall by a massless spring of stiffness 'k'. The spring is in its natural length. A constant horizontal force F starts acting on the block towards right. Find (i) speed of the block as it moves throught a distance x, (ii) speed when the block is in equlibrium and (iii) maximum extension produced in the speing.
 View Solution
View SolutionA block of mass m is connected to a spring of force constant k. Initially the block is at rest and the spring has natural length. A constant force F is applied hrizontally towards right. The maximum speed of the block will be (there is no friction between block and the surface)
 View Solution
View SolutionA block of mass m=2kg is connected to a a spring of force constant k=50N/m. Initially the block is at rest and tlhe spring has natural length. A constant force F=60N is applied horizontally towards, the maximum speed of the block (in m/s) will be (negelect friction).
 View Solution
View Solution

