Shown below is a cylinder of radius R floating in vessel containning liquids A and B Neglecting atmospheric pressure match the quantities mentioned in column-I with corresponding expression in column-II.
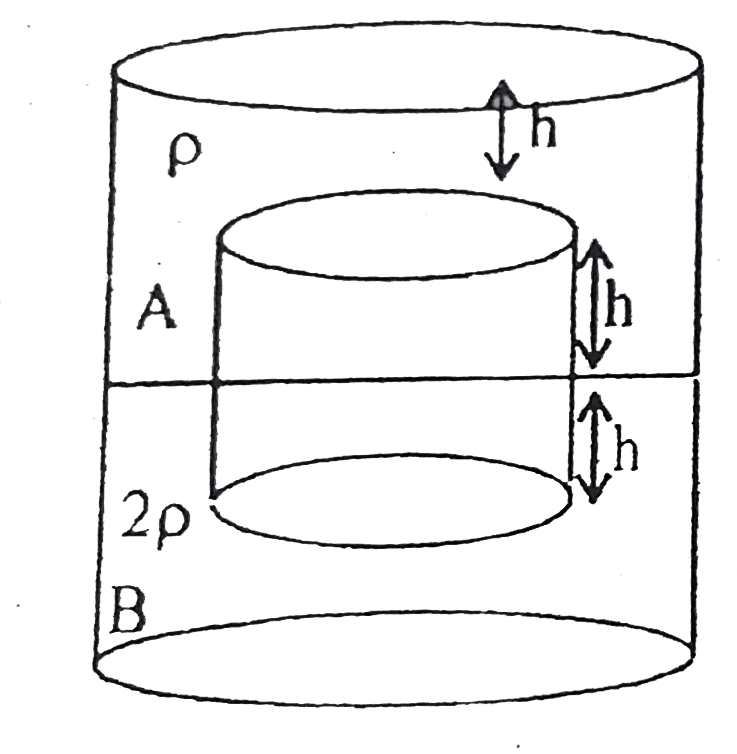
(A)
(B)
(C)
(D)
Topper's Solved these Questions
Similar Questions
Block of mass m is sliding up on the smooth inclined plane with some initial velocity Now on the block match the magnitude value of the forced on 'm' in the given directions (take the component of all the forces in the given direction)

Column -IColumn -II(a)Net force component inhorizontal direction(p) Zero(b)Net force component invertical direction(q)mgsinθcosθ(c)Net force componentalong the inclined plane(r)mgsinθ(d)Net force componentpenpendicular to the inclined plane(s)mg(1−cos2θ)View SolutionThe pressure exerted by a liquid column at rest is _______to the product of height of the liquid column,gravitational acceleration and density of the liquid.
View Solution
Knowledge Check
- Question 1 - Select One
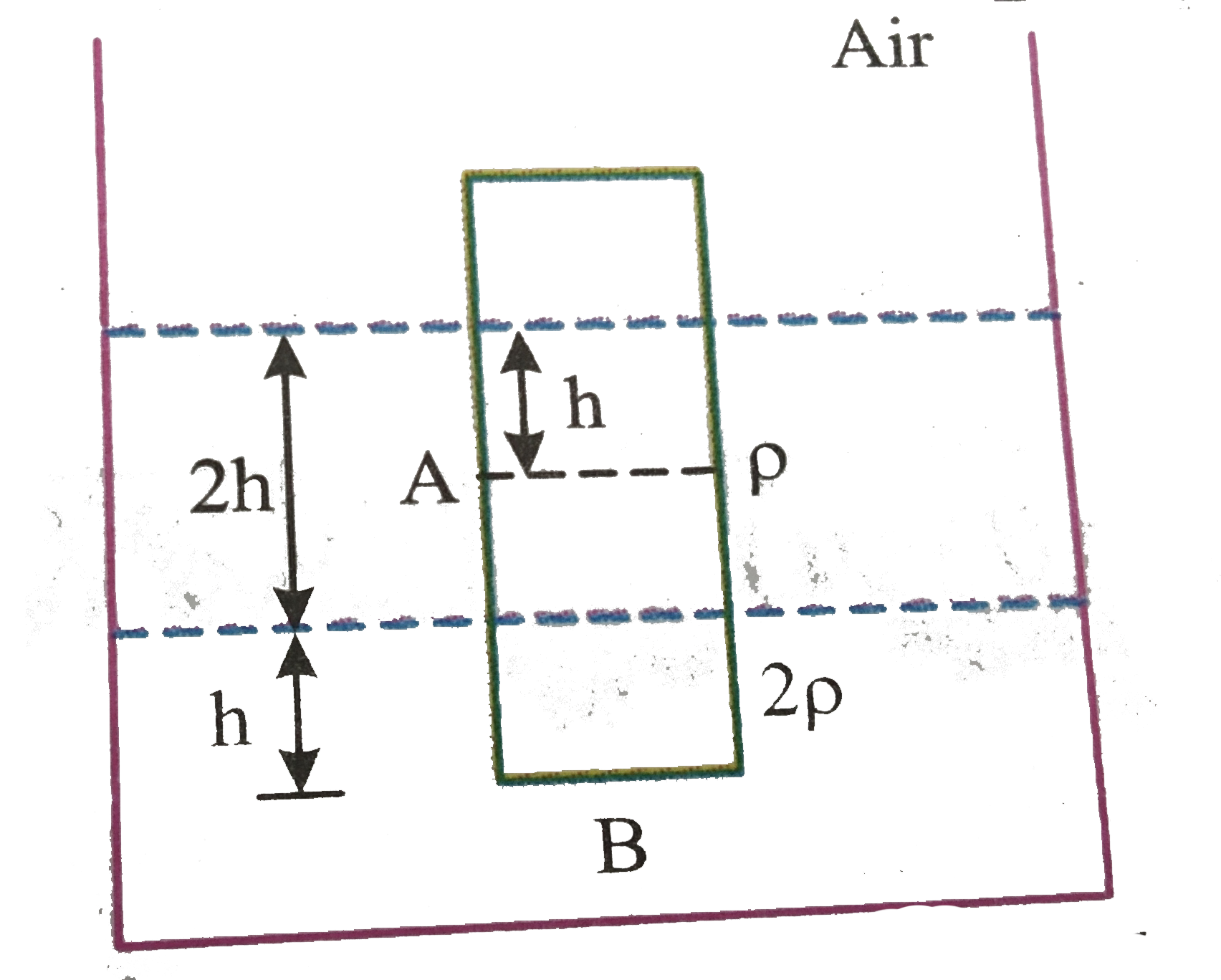
A cylinder stands vertical in two immiscible liquids of densities ρ and 2ρ as shown. Find the difference in pressure at point A and B:A2πghB3ρghC4ρghDnone - Question 2 - Select One

A spherical ball of radius R is floating at the interface of two liquids with densities ρ and 2ρ. The volumes of the ball immersed in two liquids are equal. Answer the following questions:
Find the force exerted by the liquid with density 2ρ on the ballAπR2ρg(H+2R3)B23πR2ρgC43πR2ρgD2πR2ρg(H+2R3) - Question 3 - Select One
A cylindrical vessel of radius r is filled with a homogeneous liquid upto a height h. It is found that the force exerted by the liquid column on the bottom of the cylinder is equal to the force exerted by the liquid on the sides of the cylinder. What is the relation between r and h?
Ar=h2Br=hCr=2hDr=32h
Match the types of colloidal systems given in Column I with the name given in Column II.
Column IColumn IIA.Solid in liquid1.FoamB.Liquid in solid 2.SolC.Liquid in liquid 3.GelD.Gas in liquid4.EmulsionView SolutionMatch the types of colloidal systems given in Column I with the name given in Column II.
Column IColumn IIA.Solid in liquid1.FoamB.Liquid in solid 2.SolC.Liquid in liquid 3.GelD.Gas in liquid4.EmulsionView SolutionColumn - I and Column - II contains four emtries each. Entries of Column -I are to be matched with some entries of Column - II . One or more than one entries of Column -I may have the matching with the same entries of Column - II.
column-Icolumn-II(A) Liquid dispersed in gas(P) foam (B) Gas dispersed in liquid (Q) Emulsion(C) Liquid dispersed in solid (R) Aerosol (D) Liquid dispersed in liquid (S) GelView SolutionColumn - I and Column - II contains four emtries each. Entries of Column -I are to be matched with some entries of Column - II . One or more than one entries of Column -I may have the matching with the same entries of Column - II.
column-Icolumn-II(A) Liquid dispersed in gas(P) foam (B) Gas dispersed in liquid (Q) Emulsion(C) Liquid dispersed in solid (R) Aerosol (D) Liquid dispersed in liquid (S) GelView SolutionA solid cylinder of length L is in equilibrium in two different liquid A and B as shown in the figure.The density of liquid A 3ρ2 and liquid B is 3ρ.The density of cylinder is
View Solution

