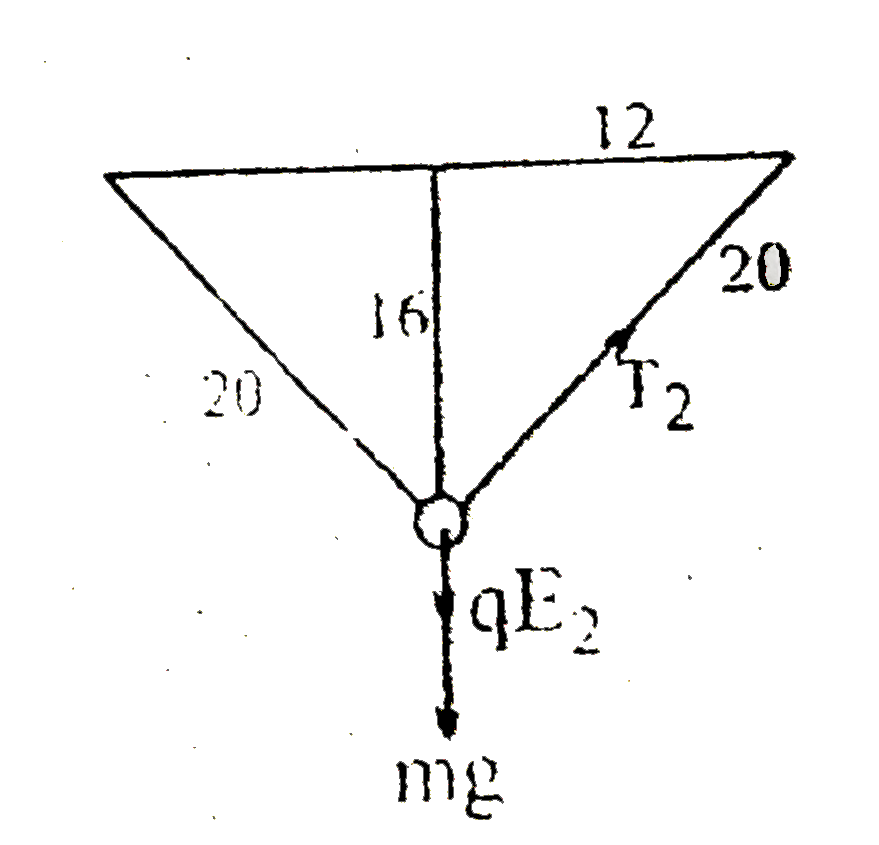
The two ends of a rubber string of negligible mass and having unstretched length 24cm are fixed at the some height as shown. A small object is attached to the string in its midpoint due to which the depression h of the object in equilibrium is 5cm. Then the small object is charged and a vertical electric field E1 is switched on in the region. The equilibrium depression of the object increases to 9cm, now the electric field is changed to E2 and the depression of object in equilibrium increases to 16cm. What is the ratio of electric field in the second case to that of in the first case ?

The correct Answer is:0017
Initially 2Tcosθ=mg…..(1)
hereT=k(26−24)
T=2k
So, 2×2k×513=mg …..(A)
1st Case Now length of string = 30 cm
T1=k(30−24)
∴2T1cosϕ=qE1+mg
2×6k×915=qE1+mg
∴365k−2013k=qE1
(468−100)k65=qE1
∴368k65=qE1 .....(B)
2nd Case T2=k(40−24)=16k
2×16k×1620=qE2+mg
∴qE2=128k5−20k13=(1664−100)k65
qE2=156465k ....(C)
:.E2E1=1564368=4.25

Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Multiple objective
131 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A small object is suspended at rest from two strings as shown in fig. The magnitude of the force exerted by each string on the object is 10√2N. Find the magnitude of the mass of the object.

View SolutionA small body attached at the end of an inextensible string completes a vertical circle , then its
View Solution
Knowledge Check
Two masses m and M are attached to the strings as shown in the figure. If the system is in equilibrium, then
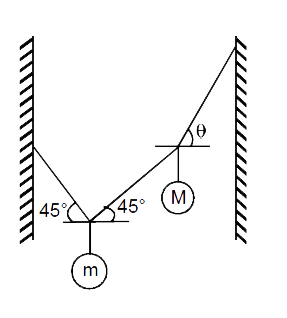 Atanθ=1+2MmBtanθ=1+2mMCcotθ=1+2MmDcotθ=1+2mM
Atanθ=1+2MmBtanθ=1+2mMCcotθ=1+2MmDcotθ=1+2mMA sphere of radius 25 cm and mass 1 kg is hung by a string of negligible mass and length 40 cm, then tension in the string is -
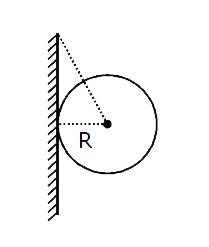 A10.81 NB18.4 NC10 ND8 N
A10.81 NB18.4 NC10 ND8 NFrom the top of a building of height h meter, the angle of depression of an object on the ground is θ. What is the distance (in meter) of the object from the foot of the building ?
AhcotθBhtanθChcosθDhsinθ
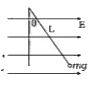
A small object with charge q and weight mg is attached to one end of a string of length 'L' attached to a stationary support. The system is placed in a uniform horizontal electric field 'E, as shown in the accompanying figure. In the presence of the field, the string makes a constant angle with the vertical. The sign and magnitude of q-
View SolutionOne end of an unstretched vertical spring is attached to the ceiling and an object attached to the other end is slowly lowered to its equilibrium position. If S is the gain in spring energy and G is the loss in gravitational potential energy in the process, then
View SolutionA small object of mass m, on the end of a light cord, is held horizontally at a distance r from a fixed support as shown. The object is then released. What is the tension in the cord when the object is at the lowest point of its swing?

View SolutionTwo masses m and M are attached with strings as shown. For the system to be in equilibrium we have.

View SolutionA small ball is suspended by a string from the ceiling of a car. As the car accelerates at a rate ‘a’ the string makes an angle 'a' with the vertical in equilibrium. Then the tension in the string is :
View Solution
