Two potentiometer wires w1 and w2 of equal length l connected to a battery of emf εP and internal resistance 'r' as shown through two switches s1 and s2. A battery of emf ε is balanced on these potentiometer wires. if potentiometer wire w1 is of resistance 2r and balancing length on w1 is l/2 when only s1 is closed and s2 is open. On closing s2 and opening s1 the balancing length on w2 is found to be (2l3) then find the resistance of potentiometer wire w2
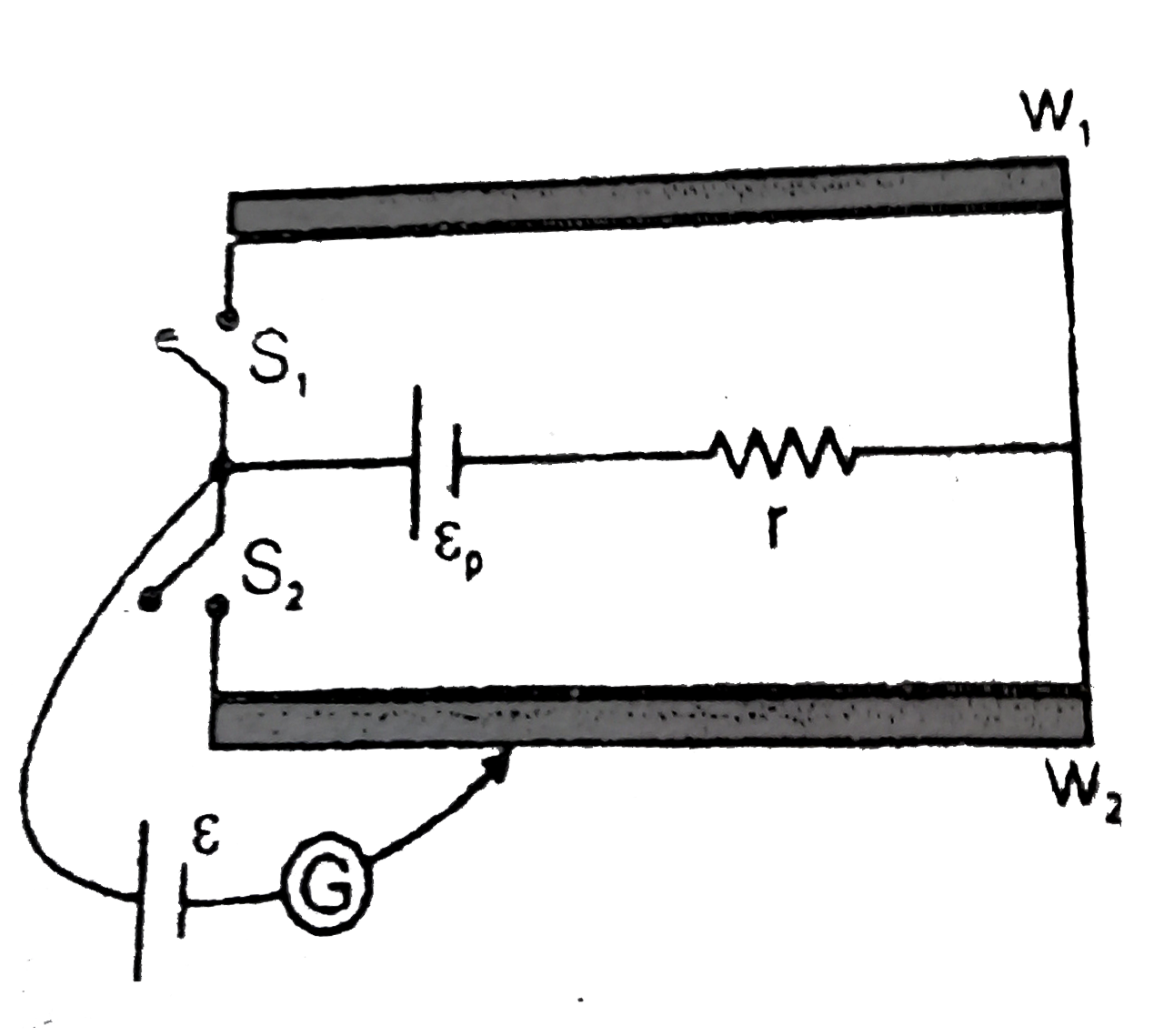
For w1,ɛ=12[ɛp1+22l]
For w2,ɛ=2l3[ɛp1+RRl]
Dividing eq (1) by (2) and on solving we get Resistance of wire w2=1Ω
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic70videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Multiple objective131videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE10videos
FLUID MECHANICS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
Two potentiometer wires w1 and w2 of equal length l, connected to a battery of emf ea and intemal resistance 1ohm through two switches s1 and sx. A battery'of emf ɛ is balanced on these potentiometer wires one by one. The potentiometer wire w1 is of rcsistance 2ohm and balancing length is I2 on it, when only s1 is closed and s2 is open. On closing s2 and opening s1, the balancing length on w2 is found to be 2l3, If the resistance of potentiometer wire w2 is given by α olum, then find 6α.
'(##CEN_KSR_PHY_JEE_CO20_E01_038_Q32##)'View SolutionA battery of emf ε and internal resistance r sends currents I1 and I2, when connected to external resistance R1 and R2 respectively. Find the emf and internal resistance of the battery.
View Solution
Knowledge Check
- Question 1 - Select One
The wire of potentiometer has resistance 4Ω and length 1m. It is connected to a cell of e.m.f. 2V and internal resistance 1Ω. The current flowing through the potentiometer wire is
A0.1AB0.2AC0.4AD0.8A - Question 2 - Select One or More
Two batteris of emf ε1 and ε2 wit respective internal resistance r1 and r2 are connected in parallel. Now
AThe effective emf of this parallel combination is (ε1r1+ε2r2)(r1+r2)BThe effective internal resistance of this combination is 2r1r2(r1+r2)Cthe effective emf of this parallel combination is (ε1r2+ε2r1)(r1+r2)DThe effective internal resistance of this combination is r1r2(r1+r2) - Question 3 - Select One
A pure inductor L, a capactior C and a resistance R are connected across a battery of emf E and internal resistance r as shows in Fig. Switch SW is closed at t=0, select the correct altermative (S).
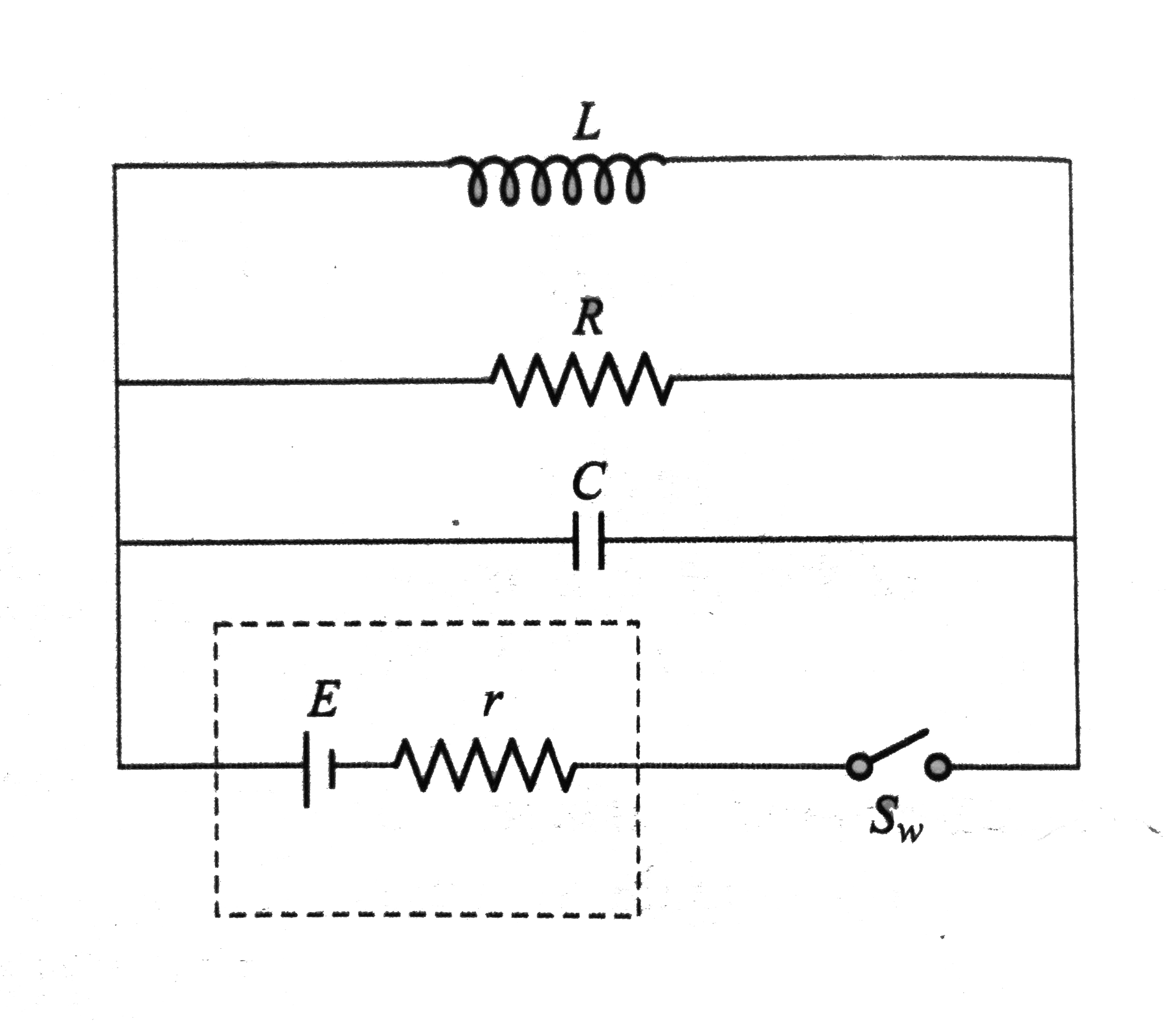 Acurrent through resistance R is zero all the timeBcurrent through resistance R is zero at t=0 and t→∞Cmaximum charge stored in the capacitor is CEDmaximum charge stored in the inductor is equal to the maximum energy stored in the capacitor
Acurrent through resistance R is zero all the timeBcurrent through resistance R is zero at t=0 and t→∞Cmaximum charge stored in the capacitor is CEDmaximum charge stored in the inductor is equal to the maximum energy stored in the capacitor
A potentiometer wire of length 10m and resistance 30Ω is connected in series with a battery of emf 2.5V, internal resistance 5Ω and an external resistance R. If the fall of potential along the potentiometer wire is 50μVmm−1, then the value of R is found to be 23nΩ. What is n?
View SolutionFind the emf ε and the internal resistance r of an electric source which is equivalent to two batteries of emf's ε1 and ε2 and internal resistances r1andr2, connected in parallel.
View SolutionA potentiometer wire of length 1m and resistance 20Ω is connected in series with a 15V battery and an external resistance 40Ω . A secondary cell of emf E in the secondary circuit is balanced by 24 cm long potentiometer wire. The emf E of the cell is ,
View SolutionA cell of emf E and internal resistance r connected in the secondary gets balanced against length l of potentiometer wire. If a resistance R is connected in parallel with the cell, then the new balancing length for the cell will be
View SolutionA potentiometer wire of Length L and a resistance r are connected in series with a battery of e.m.f. E0 and a resistance r1. An unknown e.m.f. E is balanced at a length l of the potentiometer wire. The e.m.f. E will be given by :
View Solution

