If an AC voltage 100 V is applied between points A and B, then current of 1 A and phase difference between current and voltage will be $Δ ϕ = 37^{\circ}$ . IF the same voltage is applied between points B and C, then current of 5 A and $Δ ϕ = 53^{\circ}$ What will be the impedance $(\in Ω)$ in the chain, if the same voltage is applied between points A and C? Round off to nearest integer.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $0119$

$tan ϕ = \frac{w L_{1}}{R_{1}} = \frac{3}{4}$
$w L_{1} = \frac{3}{4} R_{1}$
$1 = \frac{100}{\sqrt{\frac{9}{16} R_{1}^{2} + R_{1}^{2}}}$
$R_{1} = 80 Ω ω L_{1} = 60 Ω$
$\frac{w L_{2}}{R_{2}} = \frac{4}{3} \Rightarrow w L_{2} = \frac{4}{3} R_{2}$
$5 = \frac{100}{\sqrt{\frac{16}{9} R_{2}^{2} + R_{2}^{2}}} \Rightarrow R_{2} = 12 Ω, W L_{2} = 16 Ω$
$z = \sqrt{{(w L_{1} + w L_{2})}_{1}^{2} + {(R_{1} + R_{2})}_{1}^{2}} = 119 Ω$

|

Updated on:21/07/2023

Class 12 PHYSICS MASTER PRACTICE PROBLEM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In an AC circuit $X_{C} = X_{L}$ . The phase differe3nce between the current and voltage will be
A0
B $π$
C $π / 2$
D $π / 4$
Question 2 - Select One
An Ac voltage $V = V_{0} sin 100 t$ is applied to the circuit, the phase difference between current and voltage is found to be $\frac{π}{4}$ , then
.
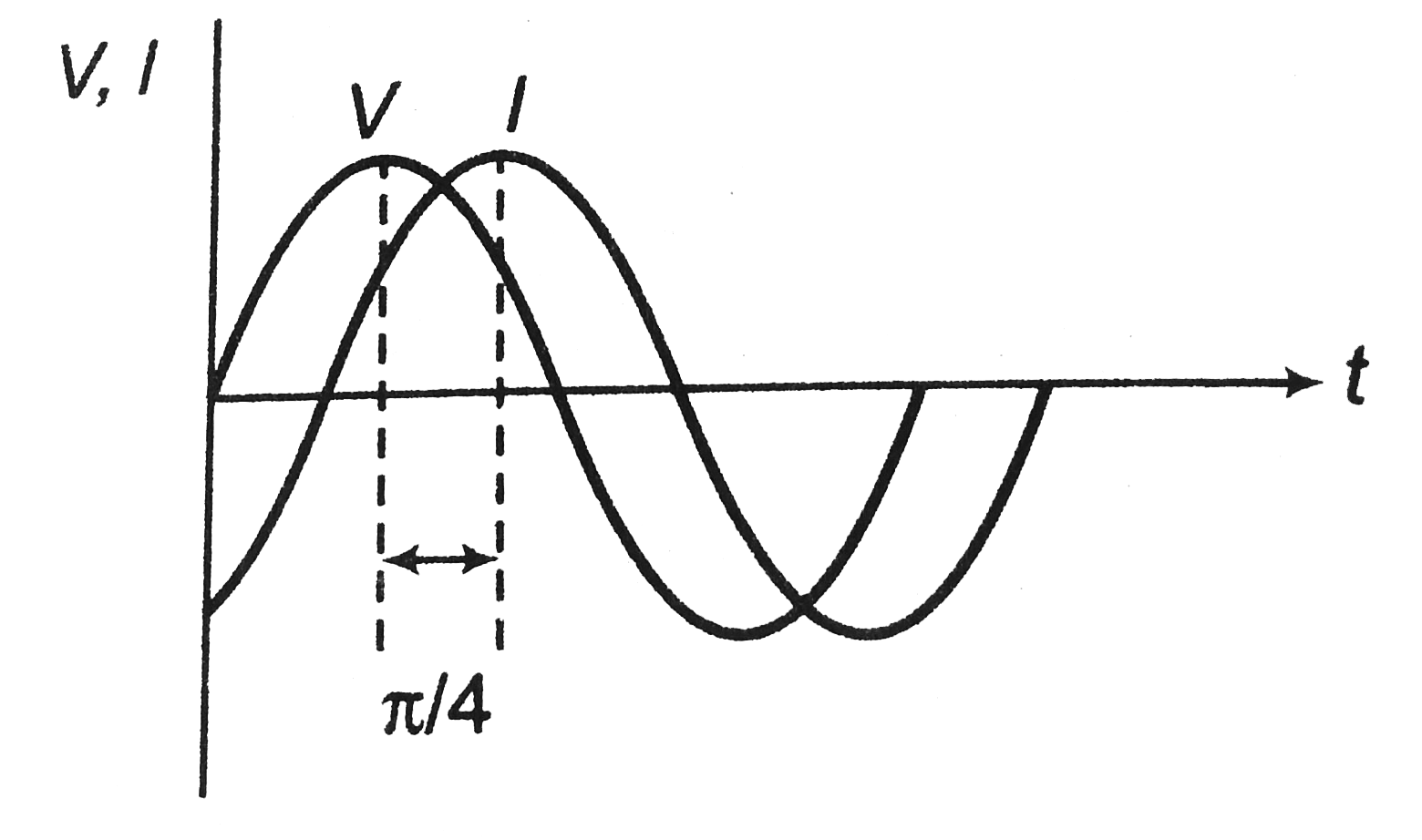A $R = 100 Ω, C = 1 μ F$
B $R = 1 Ω, C = 10 μ F$
C $R = 410 k Ω, L = 1 H$
D $R = 1 k Ω, L = 10 H$
Question 3 - Select One
The phase difference between the current and voltage of a LCR series a.c. circuit at resonance is
A0
B $\frac{π}{2}$
C $\frac{π}{4}$
D $π$

BANSAL-MASTER PRACTICE PROBLEM-Subjective

Home
Ask Doubt
Profile