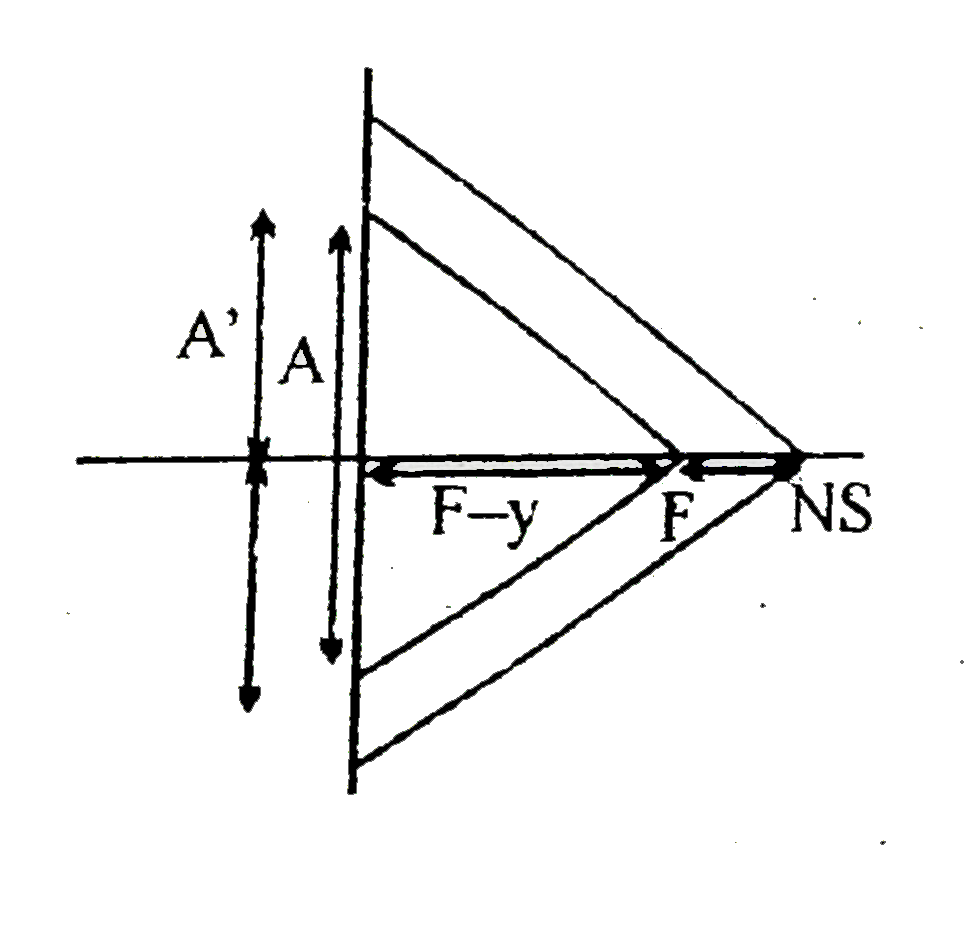
A beam of light parallel to the principal axis is focused on a screen with the help of lens, forming a circular spot with a diameter of A. If we put a plane - parallel glass plate of thickness h and refractive index n between the lens and the screen, the diameter of the bright spot on the screen increases. The diameter of the lens is d and focal length F. Find the new diameter in mm. (Take F=10 cm, A = 1 cm, n=1.5,d=2 cm, h=3 cm)
The correct Answer is:12mm

AF−y=A'F−y+h(1−1n)
A'=A[1+hF−y(1−1n)]
F−y=AFd
A'=A[1+dhAF(1−1n)]
=1[1+2×31×10(1−11.5)]=1.2cm=12mm
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Multiple objective
131 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A circular beam of light of diameter d=2cm falls on a plane refractive of glass. The angle of incidence is 60∘ and refractive index of glass is μ=3/2. The diameter of the refracted beam is
View SolutionA convex lens focuses an object 40cm from it on a screen placed 10cm away from it. A glass plate (μ=1.5) and of thickness 3cm is inserted between the lens and the screen. Where should the object be placed so that its image is again focused on the screen ?
View Solution
Knowledge Check
A circular beam of light of diameter d=2cm falls on a plane refractive of glass. The angle of incidence is 60∘ and refractive index of glass is μ=3/2. The diameter of the refracted beam is
A4.00cmB3.0cmC3.26cmD2.52cmA convex lens forms a real image on a screen placed at a distance 60 cm from the object. When the lens is shifted towards the screen by 20 cm , another image of the object is formed on the screen. The focal length of the lens is :
A45cmB40/3cmC30cmD12cmA convex lens of focal length f is placed somewhere, in between an object and a screen. The distance between the object and the screen is x. If the numerical value of the magnification produced by the lens is m, then the focal length of the lens is
Amx(m+1)2Bmx(m−1)2C(m+1)2mxD(m−1)2mx
A circular beam of light of diameter (width) falls on a plane surface of glass. The angle of incidence is .I., angle of refraction is .r. and refractive index of glass is μ. Then the diameter of the refracted beam d. is…….
View SolutionParallel beam of light of wavelength 420 nm is focused on a screen at a distance of 50 cm from the lens. What would be the radius of the central bright spot formed? Diameter of the lens is 10 cm.
View SolutionA lens with a focal length of f=30cm produces on a screen a sharp image of an object that is at a distance of a=40cm from the lens. A plane parallel plate with thickness of d=9cm is placed between the lens and the object perpendicular to the optical axis of the lens. Through what distance should the screen be shifted for the image of the object to remain distinct? The refractive index of the glass of the plate is μ=1.8.
View SolutionA lens with a focal length of f=30cm produces on a screen a sharp image of an object that is at a distance of a=40cm from the lens. A plane parallel plate with thickness of d=9cm is placed between the lens and the object perpendicular to the optical axis of the lens. Through what distance should the screen be shifted for the image of the object to remain distinct? The refractive index of the glass of the plate is μ=1.8.
View SolutionA parallel beam of light is incident on a lens of focal length 10 cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. Find the distance of the final image from the lens.
 .
.
View Solution
