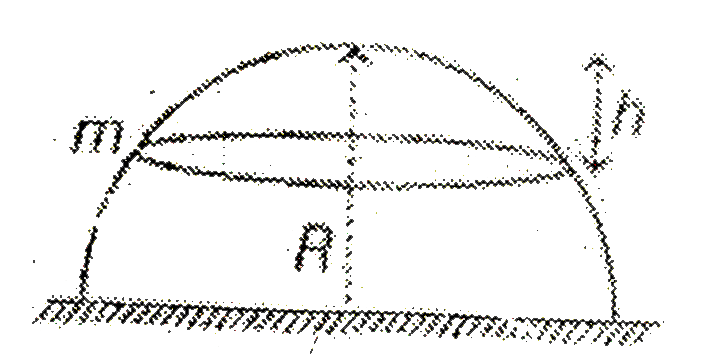
A small particle is given an initial velocity v0=10m/s along the tangent to the brim of a fixed smooth hemisphere bowl of radius r0=15√2m as shown in the figure. The particle slides on the inner surface and reaches point B, a vertical distance h=15m below A and a distance r from the vertical centerline, where its velocity v makes an angle θ with the horizontal tangent to the bowl through B. If θ=15K∘. Find the value of K. (take g=10m/s2)
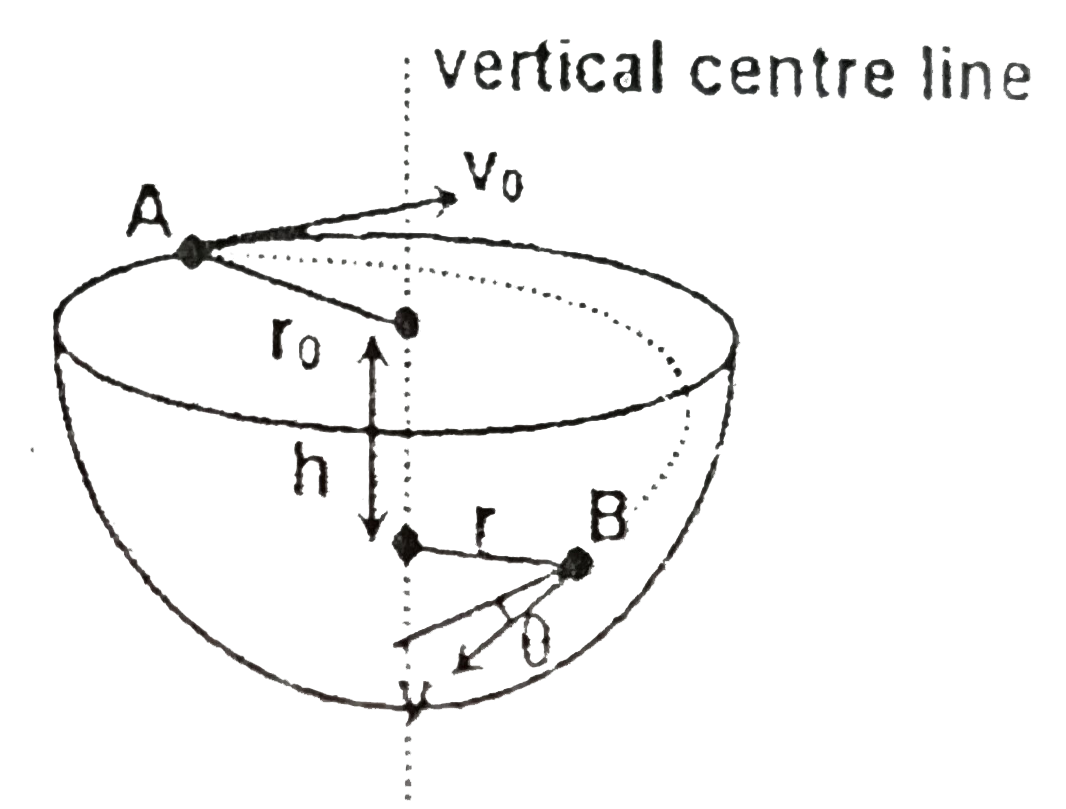
Angular momentum of the particle is conserved about the vertical central line
mv0r0=mvrcosθ
where conservation of mechanical energy gives.
12mv20+mgh=12mv2
r2=r20−h2
cosθ=1√1+2ghv20√1−h2r20

Topper's Solved these Questions
Similar Questions
A small particle is given an initial velocity v0=10m/s along the tangent to the brim of a fixed smooth hemisphere bowl of radius r0=15√2m as shown in the figure. The particle slides on the inner surface and reaches point B, a vertical distance h=15m below A and a distance r from the vertical centerline, where its velocity v makes an angle θ with the horizontal tangent to the bowl through B. If θ=15K∘. Find the value of K. (take g=10m/s2)

View SolutionA small mass particle is projected with an initial velocity v0 tangent to the horizontal rim of smooth hemispherical bowl at a radius r0 from the vertical centre line, as shown at point A. As the particle slide past point B, a distance h below A and distance r from the vertical centre line, its velocity v makes an angle θ with the horizontal tangent to the bowl through B. Determine θ.

View Solution
Knowledge Check
A small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The minimum value of v0 for which particle will be moving in a horizontal circle of radius r0.
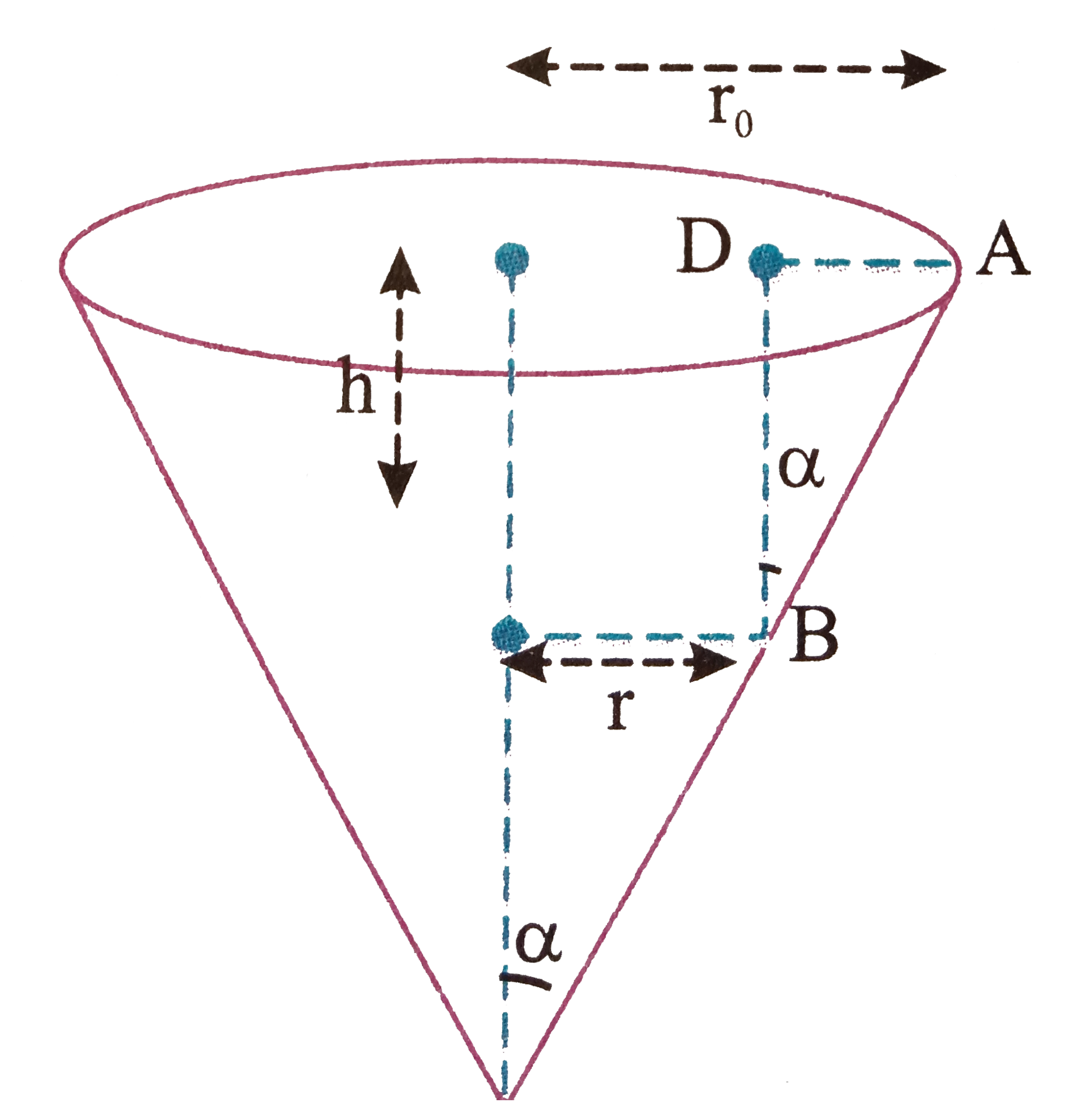 A√2gr0tanαB√gr02tanαC√gr0tanαD√4gr0tanα
A√2gr0tanαB√gr02tanαC√gr0tanαD√4gr0tanαA small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The value of θ is
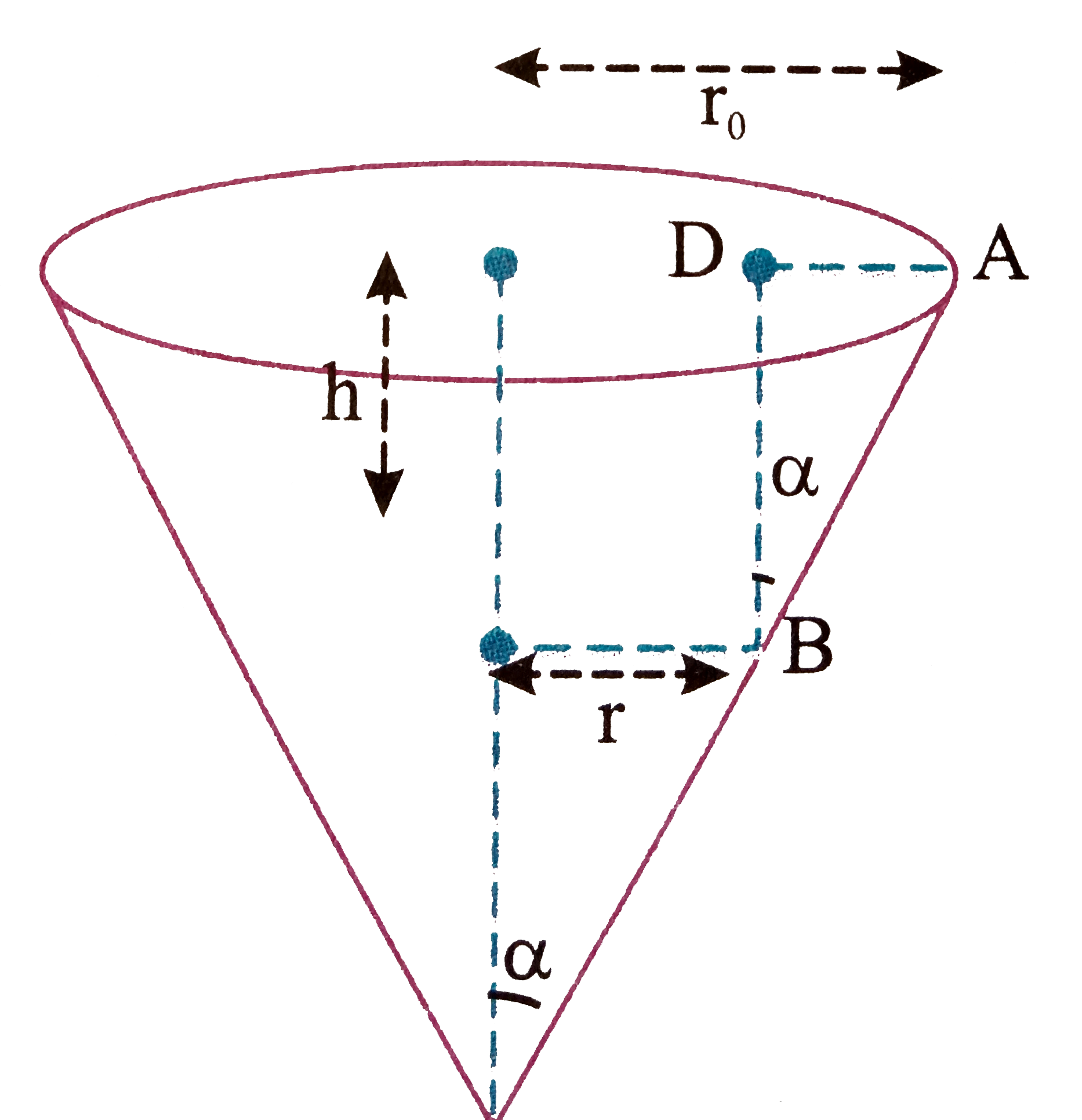 Acos−1(v0r0)(r0−htanα)√v20+2ghBcos−1(v0r0)(r0+htanα)√v20+2ghCcos−1(v0r0)(r0+htanα)√v20−2ghDcos−1(v0r0)r0√v20+2gh
Acos−1(v0r0)(r0−htanα)√v20+2ghBcos−1(v0r0)(r0+htanα)√v20+2ghCcos−1(v0r0)(r0+htanα)√v20−2ghDcos−1(v0r0)r0√v20+2ghA small particle of mass m is given an initial velocity v0 tangent to the horizontal rim of a smooth cone at a radius r0 from the vertical slides to point B, a vertical distance h below A and a distance r from the vertical centreline, its velocity v makes an angle θ with the horizontal tangent to the cone through B.
The speed of particle at point B
 A√v20+2ghB√v20−2ghC√v20+ghD√2v20+2gh
A√v20+2ghB√v20−2ghC√v20+ghD√2v20+2gh
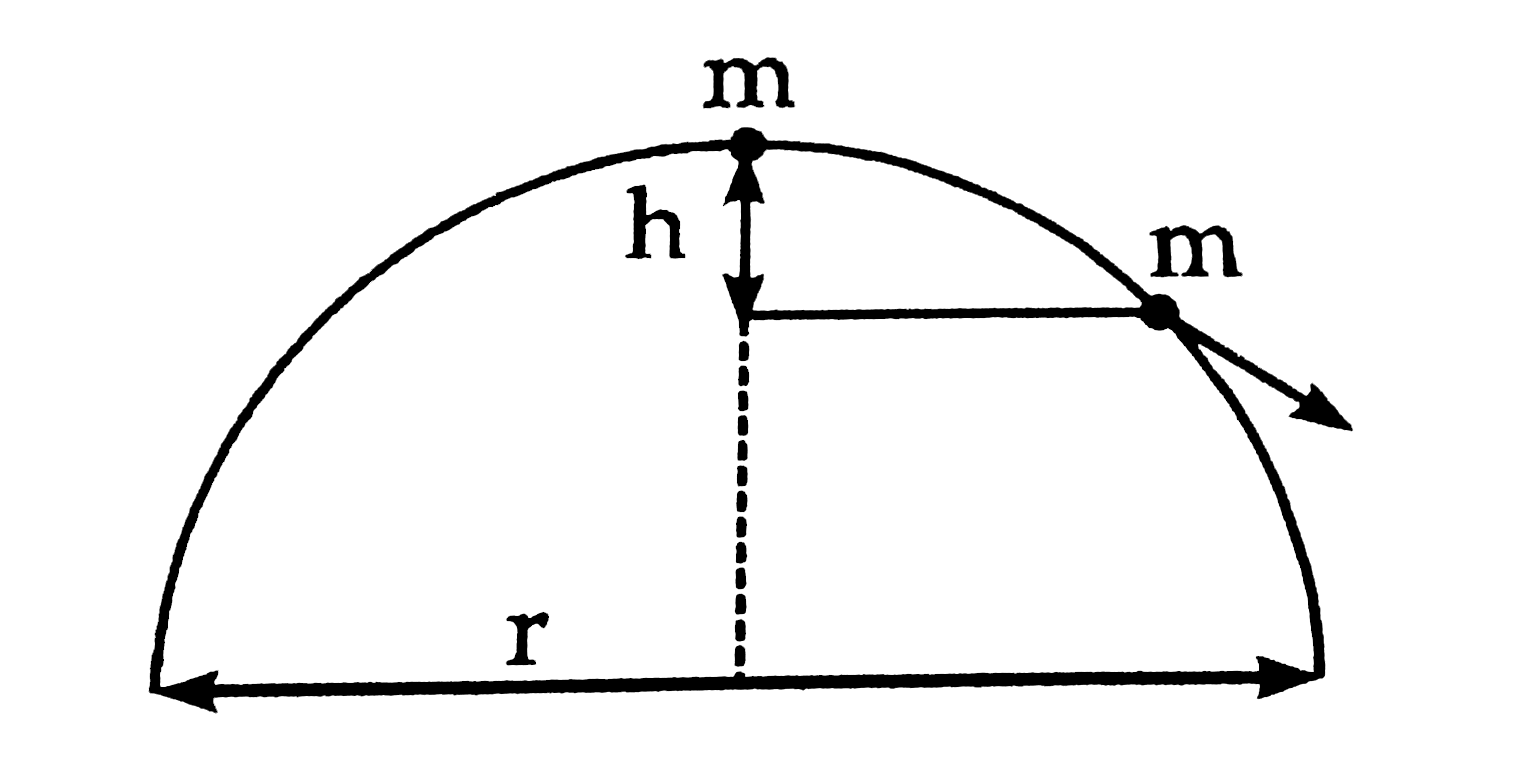
A small body of mass m slide without friction from the top of a hemispherical cup of radius r as shown in figure. If leaves the surface to the cup at vertial distance h below the highest point then
View SolutionWhat is the work done in upturning a thin hemispherical bowl as shown in the figure. The mass of the bowl is M and the radius of the bowl is R.
View SolutionA unofrom rope of mass m is placeced on a smooth fixed sphere of radius R as shown in the figure .Find the tension T in the rope when it is in a horizontal plane at a vertical distance h=R/2 below the top of the sphere .
View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure Choose the wrong option.

View SolutionA small block of mass m is released from rest from position A inside a smooth hemispherical bowl of radius R as shown in figure. Choose the wrong option (s)
View Solution
