One end of the pile of chain falls vertically through a hole in its support and pull the remaining links steadily. The links which are at rest acquire the velocity of the hanging position suddenly and without loving interaction with the remaining stationery links and with the support. If the acceleration a of the falling chain is . Find . Ignore any friction.

Let the velocity of the end of the falling chain be when a length has already fallen. Taking mass per unit length of the chain as , we can write,
or
This equation may be solved by using Intergrating factor. The solution is
. where is an arbitary constant.
At , and
and
Topper's Solved these Questions
Similar Questions
A chain of length l and mass m is lumped over the hole in a horizontal plate and a short length hangs down the hole when the chain is at rest. If it is released from this position find the velocity when the last link of the chain leaves the hole.
View SolutionA very flexible uniform chain of mass M and length l is suspended vertically in a lift so that its lower end is just touching the surface of the floor. When the upper end of the chain is released, it falls with each link coming to rest the instant it strikes the floor of the lift.Find the force exerted by the floor of the lift on the chain at the moment, when one fourth of the chain has already rested on the floor. Assume that lift is moving up with an acceleration g/2.
View SolutionA chain (A) of length L is coiled up on the edge of a table. Another identical chain (B) is placed straight on the table as shown. A very small length of both the chains is pushed off the edge and it starts falling under gravity. There is no friction

(a) Find the acceleration of the chain B at the instant L2 length of it is hanging. Assume no kinks in the chain so that the entire chain moves with same speed.
(b) For chain A assume that velocity of each element remains zero until it is jerked into motion with a velocity equal to that of the falling section. Find acceleration of the hanging section at the instant a length l0 has slipped off the table and its speed is known to be v0 at the instant.
View SolutionA uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F(figure).
Find the maximum magnitude of the force F which still does not bring about any sliding of the cylinder, if the coefficient of friction between the cylinder and the planks is equal to k. What is the acceleration wmax of the axis of the cylinder rolling down the inclined plane?

View SolutionA uniform solid cylinder of mass m rests on two horizontal planks. A thread is wound on the cylinder. The hanging end of the thread is pulled vertically down with a constant force F.
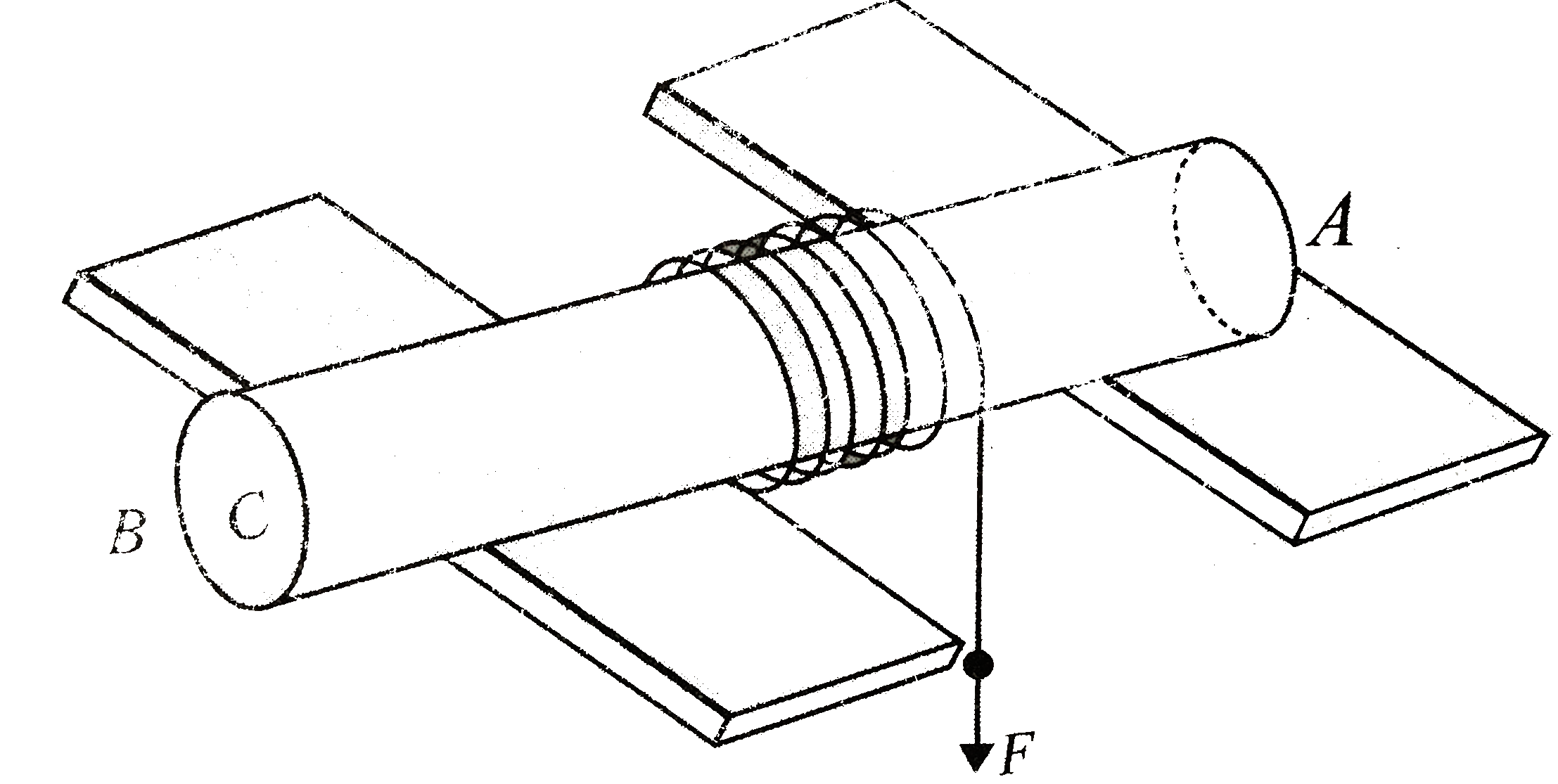
Find the maximum magnitude of the force F which may be applied without bringing about any sliding of the cylinder, if the coefficient of friction between the plank and the cylinder is equal to μ. What is the maximum acceleration of the centre of mass over the planks?
View SolutionA chain of length L is supported at one end and is hanging vertically when it is released. All of the chain falls freely with acceleration g. The moment, the chain is released a ball is projected up with speed u from a point 2 L below the point of support. Find the interval of time in which the ball will cross through the entire chain.
View SolutionA very flexible chain of mass M and length l is suspended vertically in a lift so that its lower end is just touching the surface of the floor. When the upper end of the chain is released, it falls with each link coming to rest intantaneously find the force exerted by the floor of the lift on the chain at the moment when one fourth of the chain has already landed on the floor Assume the lift is moving with acceleration g/2
View SolutionA very flexible unifrom chain of mass M and length L is suspended vertically so that its lower end just touches the surface of a table When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table Find the force exerted by the chain on the table at the moment when x part of chain has already rested on the table .
View SolutionA very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
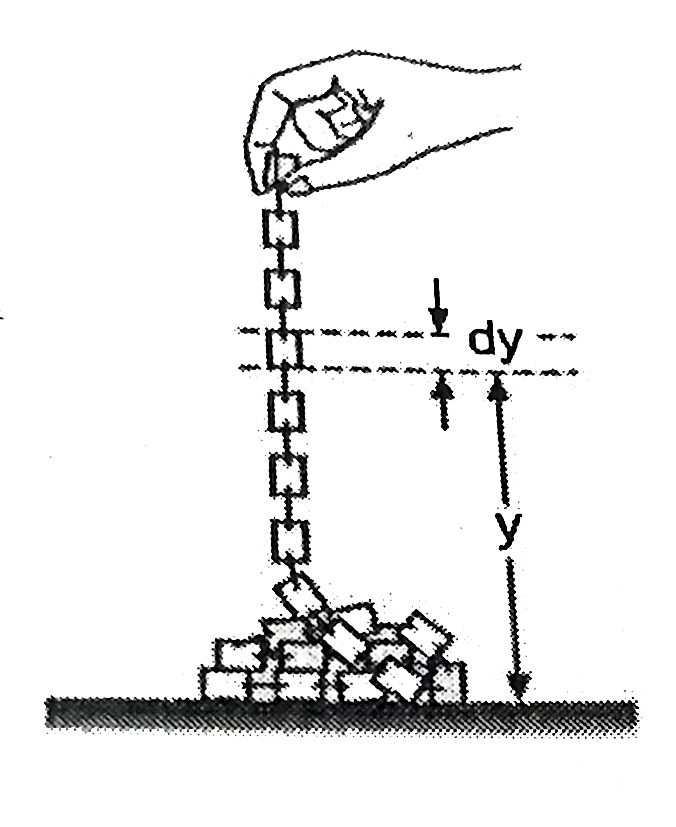
View SolutionA very flexible uniform chain of mass M and length L is suspended vertically so that its lower and just touches the surface of a table. When the upper end of the chain is released it falls with each link coming to rest the instant it strikes the table. Find the force exerted by the chain on the table at the moment when y part of the chain has already rested on the table.
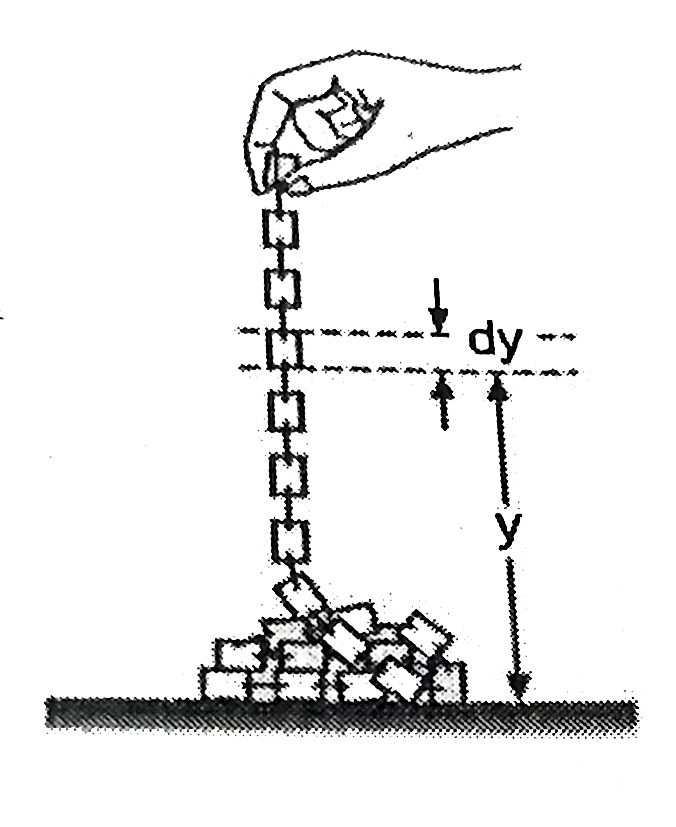
View Solution
