A disc 'A' of mass M is placed at rest on the smooth incline surface of inclination θ. A ball B of mass m is suspended vertically from the centre of the disc. A by a light inextersible string of length l as shown in the figure. If the acceleration of the disc B immediately after the system is released from rest is (M+km)gsin2θM+msin2θ. Find k.
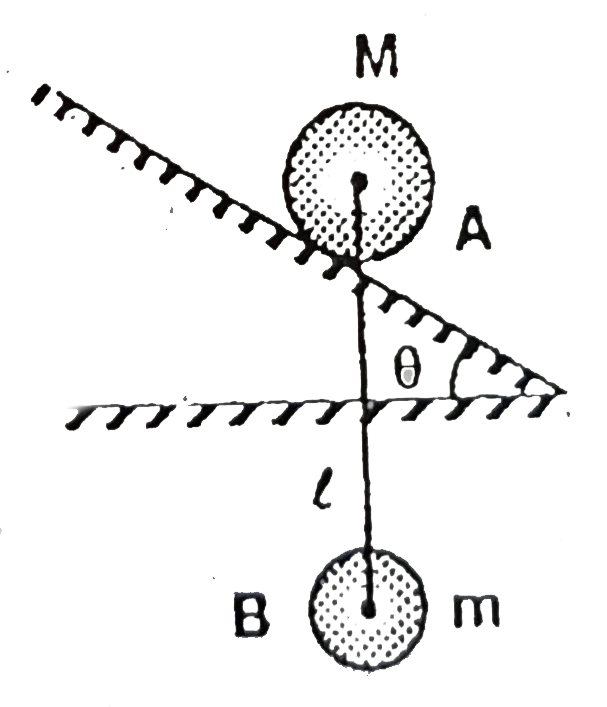
Mgsinθ+Tsinθ=Ma
mg−T=masinθ
solving, we get
a=(M+m)gsin2θM+msin2θ

Topper's Solved these Questions
Similar Questions
Knowledge Check
In the system shown all the surfaces are frictionless while pulley and string are massless. The mass of block A is 2m and that of block B is m. The acceleration of block B immediately after system is released from rest is
 Ag/2BgCg/3DNone of these
Ag/2BgCg/3DNone of theseA triangular prism of mass m placed on it is released from rest on a smooth inclined plane of inclination θ The block does not slip on the prism. Then
 AThe accelaration of the prism is gcosθBThe accelaration of the prism is gtanθCThe minimum coefficient of friction between the block the block and the prism is μmin=cotθDThe minimum coefficient of friction between the block the block and the prism is μmin=tanθ
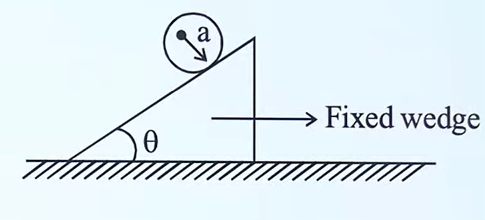
AThe accelaration of the prism is gcosθBThe accelaration of the prism is gtanθCThe minimum coefficient of friction between the block the block and the prism is μmin=cotθDThe minimum coefficient of friction between the block the block and the prism is μmin=tanθA string is wrapped on a uniform disc and the other end of the string connected to a wall. The system is placed on a smooth plane, inclined at an angle θ, with the string parallel to the plane, as shown in the figure. The acceleration of the disc is
 A13gsinθB12gsinθC23gsinθD13gsinθ
A13gsinθB12gsinθC23gsinθD13gsinθ
In the system shown all the surfaces are frictionless while pulley and string are massless. The mass of block A is 2m and that of block B is m. The acceleration of block B immediately after system is released from rest is

View SolutionA triangular prism of mass m placed on it is released from rest on a smooth inclined plane of inclination θ The block does not slip on the prism. Then

View SolutionA string is wrapped on a uniform disc and the other end of the string connected to a wall. The system is placed on a smooth plane, inclined at an angle θ, with the string parallel to the plane, as shown in the figure. The acceleration of the disc is

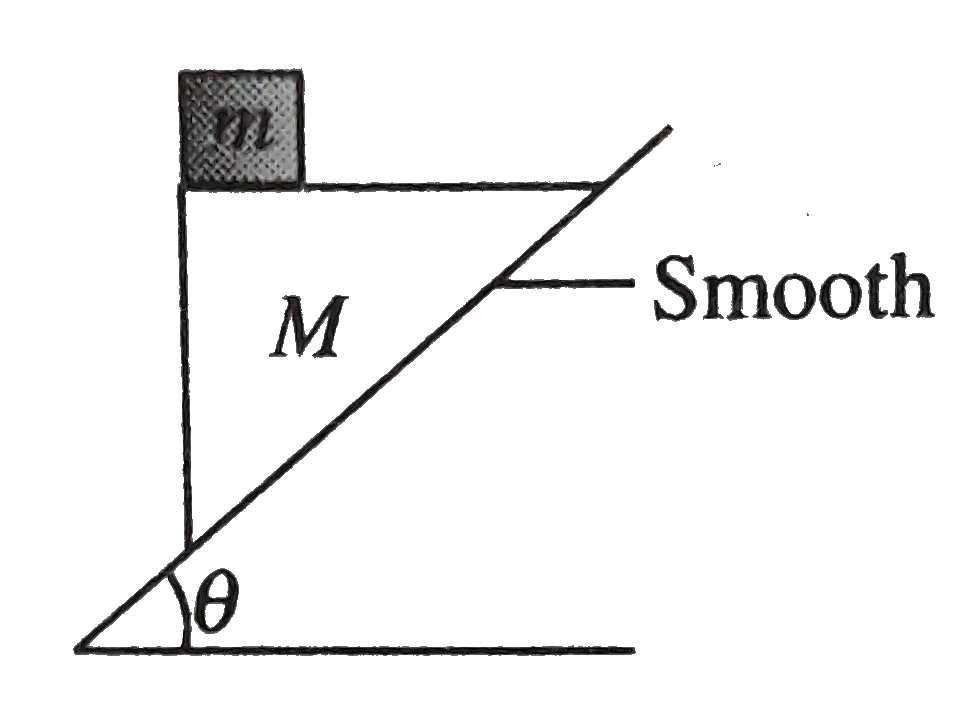
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released

View SolutionA block of mass m is placed on a smooth wedge of inclination θ & mass M. The whole system is slip on the wedge. Then the normal reaction on the wedge acting from the ground :
View Solution