A laser beam propagates through a spherically symmetric medium, as shown in the figure. The refractive index varies with the distance to the symmetry centre C by the law μ(r)=μ0rr0, where μ0=1, r0=3cm, r0≤r<∞. The beam's trajectory lies in the plane that includes C. At distance r1=8√2cm the beam makes an angle ϕ=30∘ with →r1 as shown in the figure. Find the minimum distance (in cm) the beam reach relative to the symmetry centre C.

Video Solution
Text Solution
μ1sinϕ=μ2sinθ
r1sinθ'=r2sinθ
sinϕ=r2r1sinθ'
μ1sinϕ=μ2r2r1sinθ'
r1μ1sinϕ=r2μ2sinθ'
r1μ0r1r0sin30∘=μ0r2minr0sin90∘ (At minimum separation)
rmin=r1√sin30∘=8cm

|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
A cyclist rides along the circular path of a circular horizontal plane of radius R, the firctional coefficient being dependent only on distance r from the centre O of the plane as μ=μ0(1−rR), where μ0 is a constant.
What is the cyclist's maximum velocity ?A√μRgB2√μ0RgC12√μ0RgD√2μ0Rg - Question 2 - Select One
A cyclist rides along the circular path of a circular horizontal plane of radius R, the firctional coefficient being dependent only on distance r from the centre O of the plane as μ=μ0(1−rR), where μ0 is a constant.
Find the radius of the circle such that the cyclist can ride with the maximum velocity.ARBR2CR3DR4 - Question 3 - Select One
A current /is flowing through the loop. The direction of the current and the shape of the loop are as shown in the figure. The magnetic field at the centre of the loop is μ0IR×(MA=R,MB=2R,∠DMA=90∘
 A516 ,but of the plane of the paper.B516, but into the plane of the paper.C716,but out of the plane of the paper.D716,but into the plane of the paper.
A516 ,but of the plane of the paper.B516, but into the plane of the paper.C716,but out of the plane of the paper.D716,but into the plane of the paper.
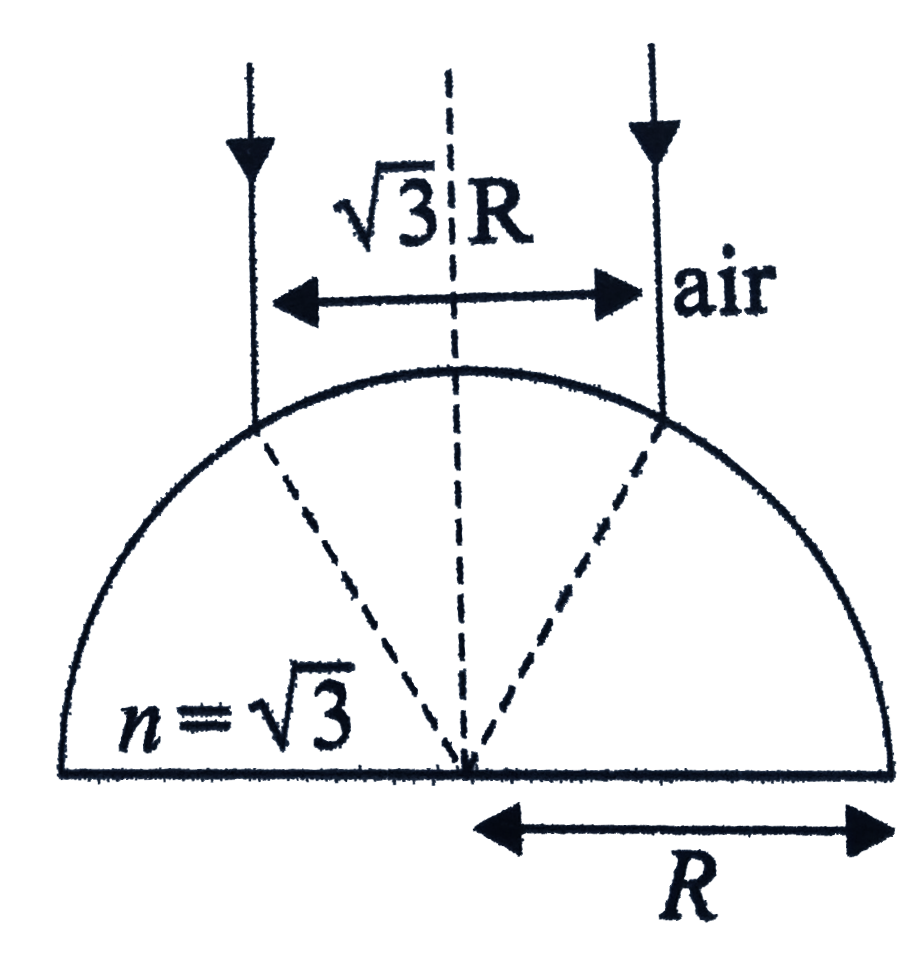
A light beam of diameter √3R is incident symmetrically on a glass hemispher of radius R and of refractive index n=√3 . Find radius of the beam at the base of hemispher.
 View Solution
View SolutionThe mass density of a planet of radius R varie with the distance r form its centre as ρ(r)=p0(1−r2R2). Then the graviational field is maximum at :
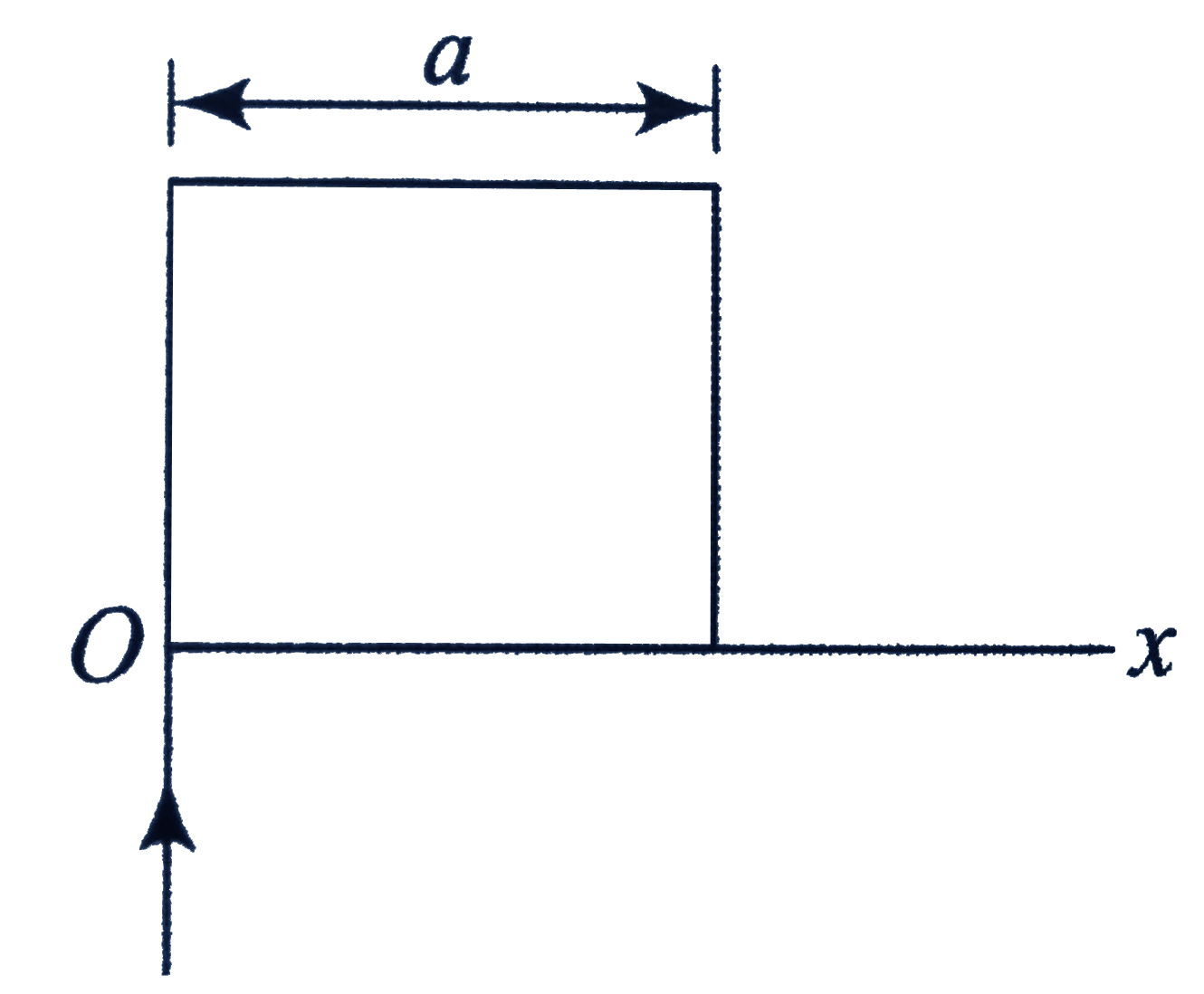
View SolutionThe refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
 View Solution
View SolutionR=R0A1/3, where R0 has the value:
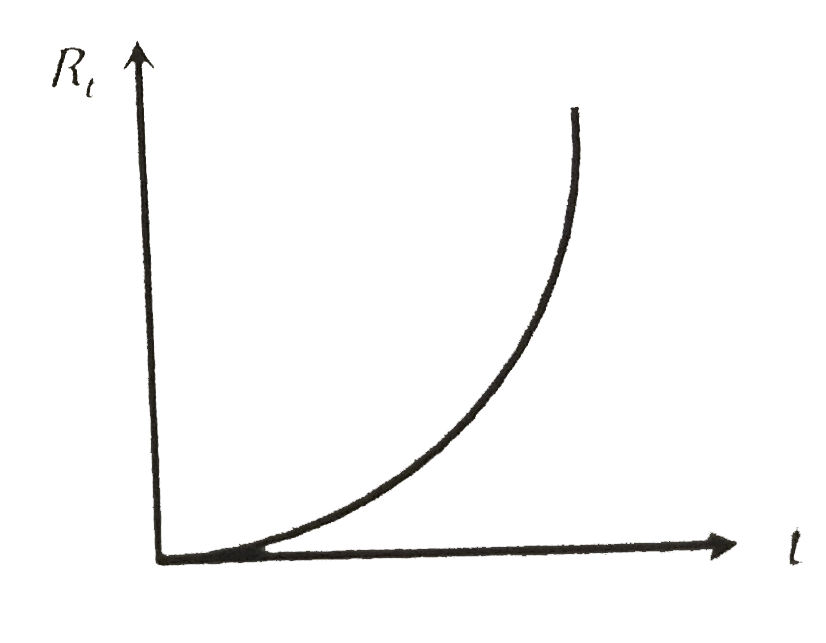
View SolutionThe resistance t R of a conductor varies with temperature t as shown in the figure. If the variation is represented by Rt=R0[1+αt+βt2], then
 View Solution
View Solution

