Two particles A and B are situated at point (60,0) at t=0. The particle A move on a circle given by X2+Y2=3600 and with a speed 6πm/s, while B moves with a constant velocity.
(a) Find the velocity of B so that the collision takes places between A and B at point (60,0).
(b) Calculate average acceleration of particle A during the motion.
(a) Time for A to move from (0,60) to (60,0)
=2π×604×16π=5 second.
Displacement of B=60ˆi−60ˆj
∴ Velocity of B=(60ˆi−60ˆj)/5=12(ˆi−ˆj)m/s
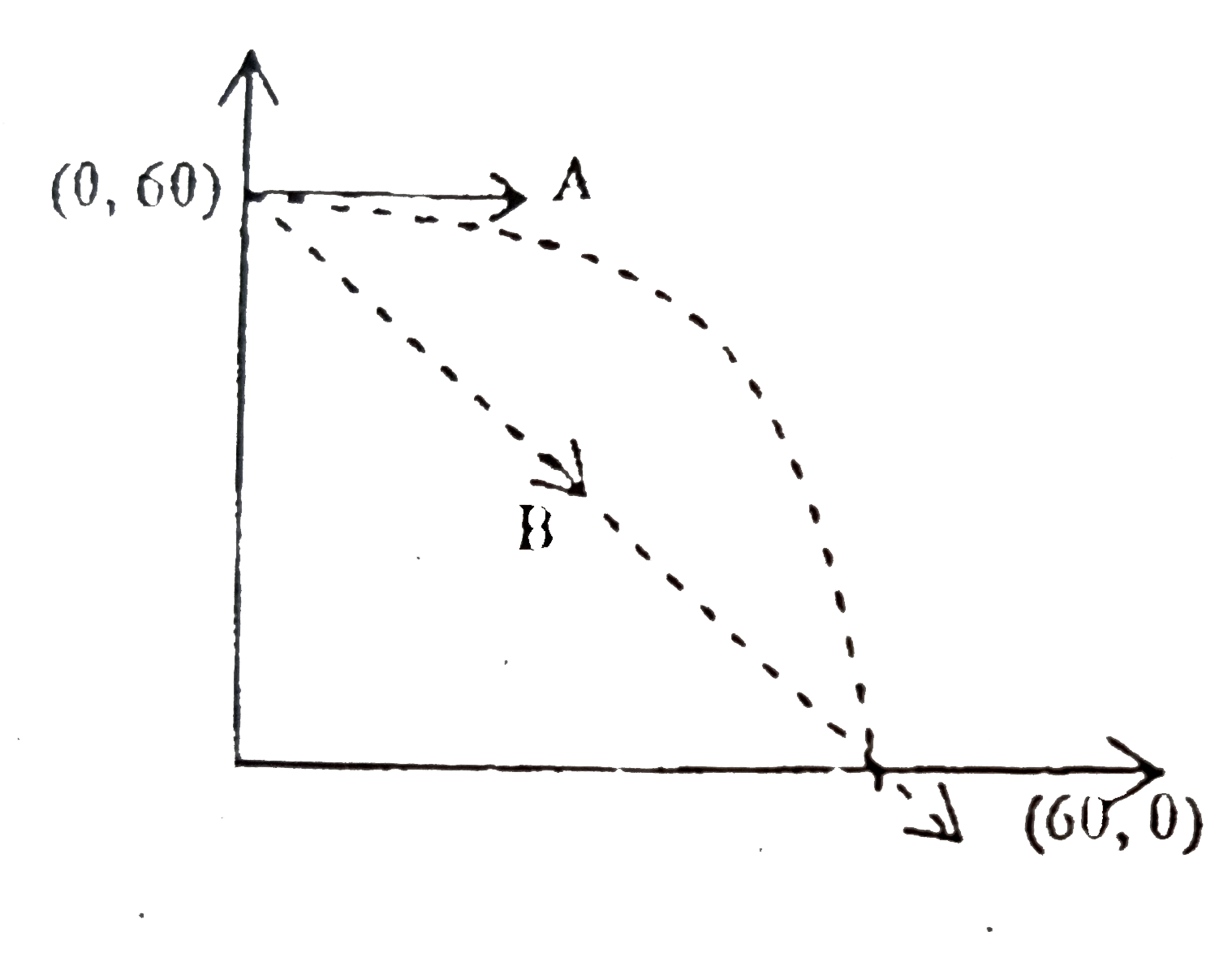
(b) →aavg of A=Δ→vt=−6πˆj−6πˆi5=−6π5[ˆi+ˆj]m/s2
Topper's Solved these Questions
Similar Questions
A particle moves in a circle of radius R=2122m with constant speed 1m/s. Find,
(a) magnitude of average velocity and
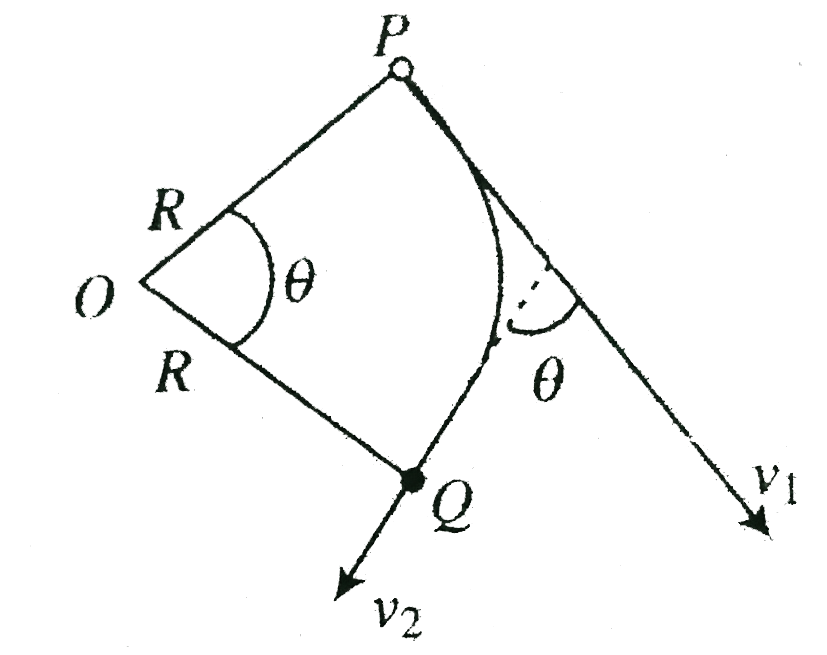
(b) magnitude of average acceleration in 2 s.View SolutionA particle describes an angle θ in a circular path with a constant speed v. Find the a charge in the velocity of the particle and b average acceleration of the particle during the motion in the curve (circle).
. View Solution
Knowledge Check
- Question 1 - Select One
A particle moves from A to B with a uniform velocity v1 and from B to A with a velocity v2. If it moves along a straight line between A and B, then the average velocity of the particle is
Av1v22Bv1+v22C2v1v2v1+v2Dzero - Question 2 - Select One
Two particles A and B are located at point (0m,50m) at t=0. The particle A moves withy a constant velocity and the particle B moves on a circle of radius 50 m having centre at origin (0,0) as shown in figure. The pasrticle B has a constant speed 5πm/s. What will be the velocity of particle A so that both the pasrticles reach at point (50m,0m) simultaneously.
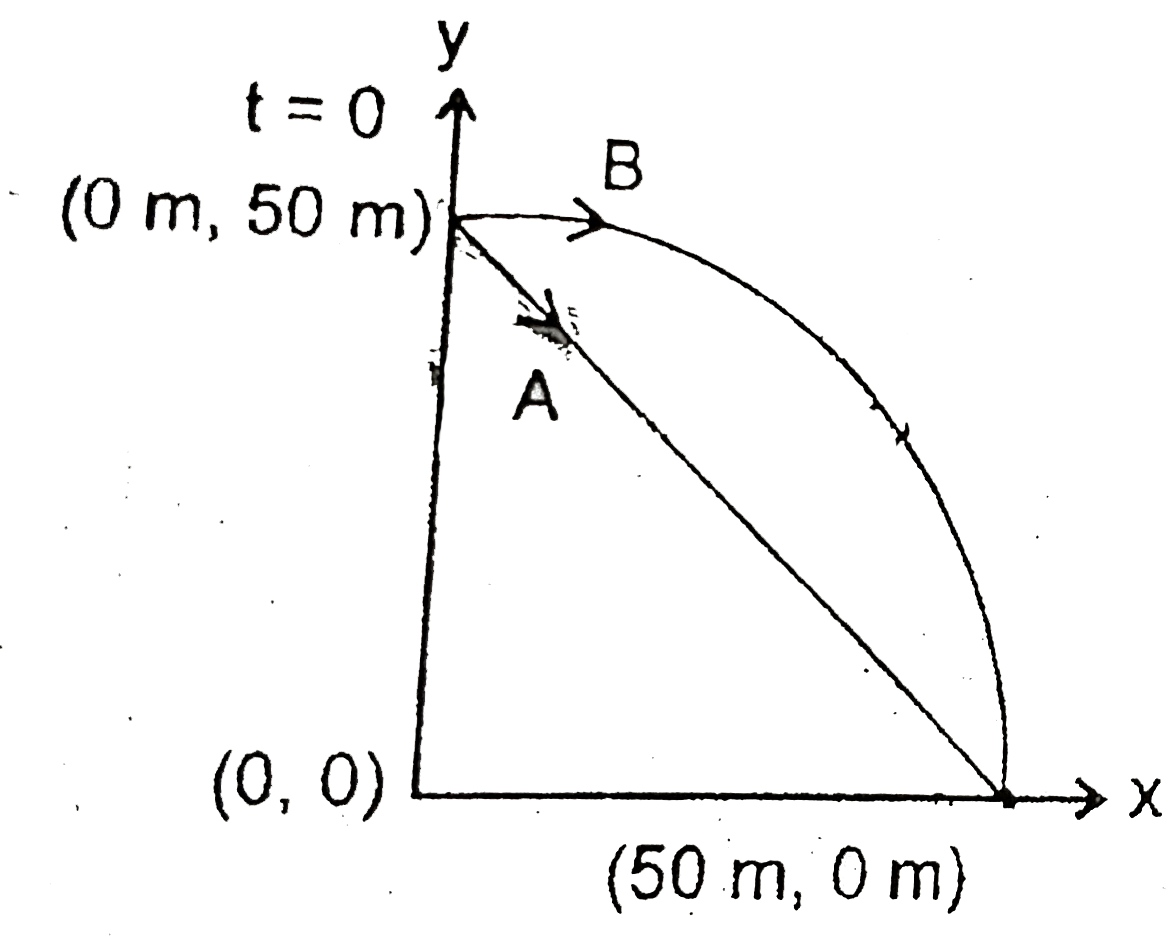A10√3(ˆi−ˆj)m/sB5√3(ˆi−ˆj)m/sC10(ˆi−ˆj)m/sD5(ˆi−ˆj)m/s - Question 3 - Select One
A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
A particle of mass m is moving with constant velocity v0 along the line y=b. At time t=0 it was at the point (0,b). At time t=bv0, the
View SolutionA particle is moving in a circle of radius having centre at 0. with a constant speed V. The magnitude at change in velocity in moving from A to B is 60°
View SolutionTwo particles move simultaneously from two points A and B, 300m apart. The particle at A, starts towards B with a velocity of 25 m/s and that at B, moves normal to the former with a velocity of 20 m/s
View SolutionTwo particles A and B separated by 10 m at time t=0 are moving uniformly. A is moving along line AB at a constant velocity of 4m/s and B is moving perpendicular to the velocity of A at a constant velocity of 5m/s. After what time the two particles will be nearest to each other?
View SolutionTwo particles AandB move on a circle Initially, particles AandB are diagonally opposite to each other. Particle A moves with angular velocity πrads−1 and angular acceleration π/2rads−2 and particle B moves with constant angular velocity 2πrads−2. Find the time after which both the particlsd AnadB will collide.
View Solution