A particle is projected from the mid-point of the line joining two fixed particles each of mass m. If the separation between the fixed particles is l, the minimum velocity of projection of the particle so as to escape is equal to
√GMl
√GM2l
√2GMl
2√2GMl
To find the minimum velocity of projection of a particle so as to escape the gravitational influence of two fixed particles, we can follow these steps:
1. Understanding the Setup:
- We have two fixed particles, each of mass m, separated by a distance l.
- A third particle (also of mass m) is projected from the midpoint of the line joining the two fixed particles.
2. Position of the Third Particle:
- The midpoint between the two fixed particles is at a distance of l2 from each fixed particle.
3. Gravitational Potential Energy:
- The gravitational potential energy U between two masses is given by:
U=−Gm1m2r
- For the third particle at the midpoint, the potential energy due to each fixed particle is:
U1=−Gmml2=−2Gm2l
- Since there are two fixed particles, the total potential energy U is:
U=U1+U2=−2Gm2l−2Gm2l=−4Gm2l
4. Kinetic Energy:
- The kinetic energy K of the particle when it is projected with velocity V is given by:
K=12mV2
5. Condition for Escape:
- For the particle to escape the gravitational influence of the two fixed particles, the total mechanical energy (kinetic + potential) must be zero or greater:
K+U≥0
- Substituting the expressions for K and U:
12mV2−4Gm2l≥0
6. Solving for Minimum Velocity:
- Rearranging the equation gives:
12mV2≥4Gm2l
- Dividing both sides by m (assuming m≠0):
12V2≥4Gml
- Multiplying both sides by 2:
V2≥8Gml
- Taking the square root:
V≥√8Gml
7. Final Expression for Minimum Velocity:
- Thus, the minimum velocity V required for the particle to escape is:
V=2√2Gml
Final Answer:
The minimum velocity of projection of the particle so as to escape is:
V=2√2Gml
- We have two fixed particles, each of mass m, separated by a distance l.
- A third particle (also of mass m) is projected from the midpoint of the line joining the two fixed particles.
- The midpoint between the two fixed particles is at a distance of l2 from each fixed particle.
- The gravitational potential energy U between two masses is given by:
U=−Gm1m2r
- For the third particle at the midpoint, the potential energy due to each fixed particle is:
U1=−Gmml2=−2Gm2l
- Since there are two fixed particles, the total potential energy U is:
U=U1+U2=−2Gm2l−2Gm2l=−4Gm2l
- The kinetic energy K of the particle when it is projected with velocity V is given by:
K=12mV2
- For the particle to escape the gravitational influence of the two fixed particles, the total mechanical energy (kinetic + potential) must be zero or greater:
K+U≥0
- Substituting the expressions for K and U:
12mV2−4Gm2l≥0
- Rearranging the equation gives:
12mV2≥4Gm2l
- Dividing both sides by m (assuming m≠0):
12V2≥4Gml
- Multiplying both sides by 2:
V2≥8Gml
- Taking the square root:
V≥√8Gml
- Thus, the minimum velocity V required for the particle to escape is:
V=2√2Gml
The minimum velocity of projection of the particle so as to escape is:
V=2√2Gml
Topper's Solved these Questions
Similar Questions
A particle of mass 1kg and charge 1/3μC is projected toward a nonconducing fixed spherical shell of radius r=1mm having the same charge uniformly distributed on its surface. Find th minimum initial velocity of projection requires if the particle just grazes the shell.
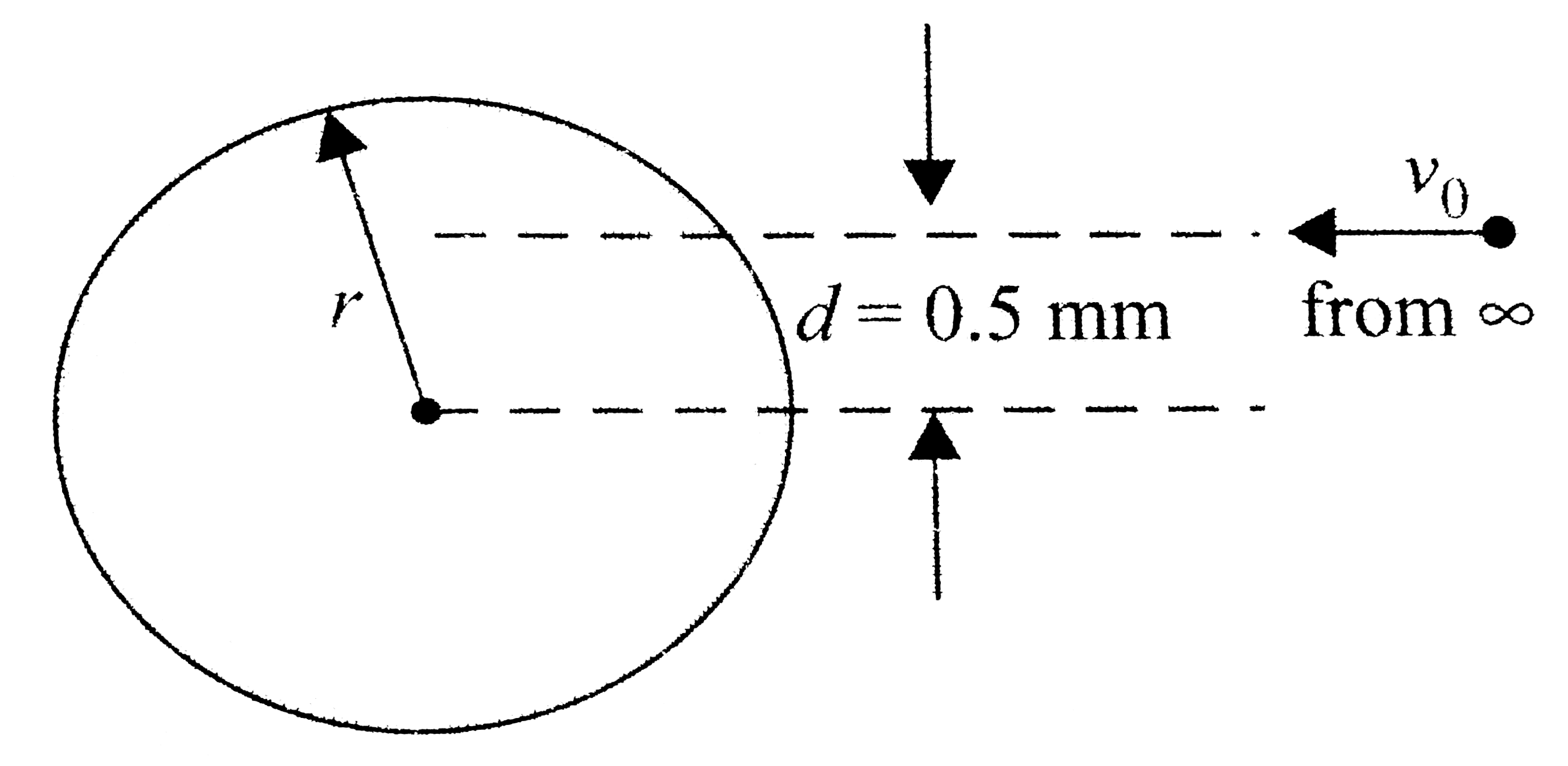 .
.
View SolutionA particle P is to be projected from a fixed point A on the ground with a fixed speed u. Another particle Q is also to be projected from a point B which is directly above the point A. The trajectory of the particle Q touches all possible trajectories (for different angle of projection) of the particle P in the vertical x−y plane. Find the equation of trajectory of the particle Q. (Take the point A as origin, horizontal axis x− axis and vertical axis y−axis Consider the figure.)

View Solution
Knowledge Check
The escape velocity of a particle of mass m varies as :
Am∘BmCm2Dm−1The escape velocity of a particle of mass m varies as
Am2BmCm0Dm−1A particle is projected from the ground with an initial speed of v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
Av2√1+2cos2θBv2√1+2cos2θCv2√1+3cos2θDvcosθ
Does centre of mass of a system of two particles lie on the line joining the particles ?
View SolutionA particle is projected from the ground with an initial speed v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectory is [EAM2013]
View SolutionA particle is projected from a point on the level ground and its height is h when at horizontal distances aand2a from its point of projection. Find the velocity of projection.
View SolutionA charged particle +q of mass m is placed at a distance d from another charge particle −2q of mass 2m in a uniform magnetic field of induction vectro B as shown in the fig.If the particles are projected towards each other with equal speeds v.(Neglect the interaction between the particles)
(a)Find the maximum value of the projection speed Vmax so that the two particles do not collide.
b)Find the time interval after which collision occurs between the particles if projection speed equals 2Vmax
(c)In the previous part,assuming that the particles stick after the collision find the radius of the circular path of the particle in subsequent motion.

View SolutionA particle is projected from the ground with an initial speed of 5ms−1 at an angle of projection 60° with horizontal. The average velocity of the particle between its time of projection and the time it reaches highest point of trajectory
View Solution
