A horizontally oriented bent thin tube ABC of length 1.4m rotates with a constant angular velocity ω about a stationary vertical axis OO' passing through the end A as shown in figure. The portion BC of tube is parallel to OO' and its length is equal 0.4m. At t=0, AB part of tube is filled with an ideal fluid. The end A of tube is open, the closed end C has a very small orifice. Find the maximum height reached by fluid relative to end C. (take g=10/s2 and ω=10rad/s)

Let any time t fluid just fills the portion BC and comes out with velocity v.
l=1m, x=0.4m
In rotating frame, centrifugal force on portion A'B,
F=ρA∫lxω2r.dr=ρAω2(l2−x2)2
Due to pressure difference difference between C and A'
ΔP=12ρω2(l2−x2−ρgx)
Now 12ρvV2=ΔP=ρω22(l2−x2)−ρgx....(1)
From Bermoulli theorem,
Let it reaches upto a height h, then,
ρgh=12ρv2=ρω2(l2−x2)2−ρgx
ρ×10×h=ρ×(10)22(12−(.4)2)−.4×10×ρ⇒h=3.8m.

Topper's Solved these Questions
Similar Questions
A horizontally oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO′ passing through the end A (figure). The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. Find the velocity of the fluid relative to the tube as a function of the column "height" h.
 View Solution
View SolutionA horizontal oriented tube AB of length l rotates with a constant angular velocity ω about a stationary vertical axis OO' passing thorugh the end A figure. The tube is filled with an ideal fluid. The end A of the tube is open, the closed end B has a very small orifice. find the velocity of the fluid relative to the tube as a function of the column height h.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A thin uniform rod of mass m and length L rotates with the constant angular velocity ω about .the vertical axis passing through the rod's suspensjon point O. It describes a carried surface, then:
Acentrifugal force acting on rod is mL2sinθω2 and will pass through centre of massBcentrifugal force acting on rod is mL2sinθω2 and will not pass through centre of massCθ=cos−1(3g2ω2L)Dθ=cos−1(gω2L) - Question 2 - Select One
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl] - Question 3 - Select One
A thin uniform copper rod of length l and cross-section area A and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. The elongation of the rod will be
Amω2l26AYBmω2l23AYCmω2l2AYDmω2l22AY
_S01_079_Q01.png)
A horizontal oriented tube AB of length 5m rotates with a constant angular velocity 0.5 rad/s about a stationary vertical axis OO' passing through the end A. the tube is filled with ideal fluid. The end of the tube is open, the closed end B has a very small orifice. The velocity with which the liquid comes out from the hole (in m/s) isView SolutionA horizontally orientd tube of length l rotates with a constant angular velocity ω about a stationary vertical axis. XX passing through end A. The tube is filled with ideal fluid.
The end A of tube is having pressure P0. The closed end B has a small hole and at time t = 0, the fluid column has length of l. Find velocity of fluid relative to tube at the instant t = 0
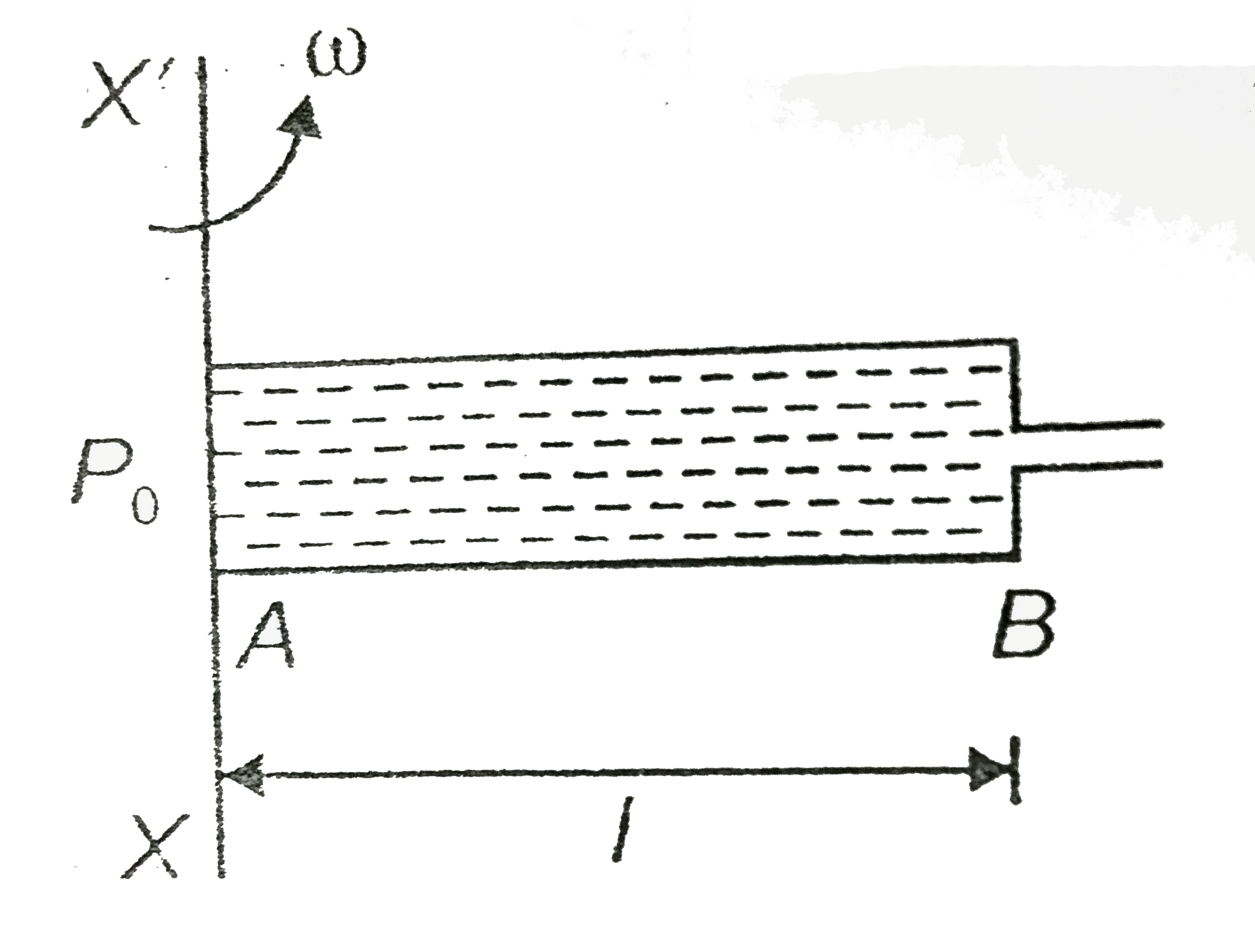 View Solution
View SolutionA horizontal tube with closed ends is rotated with a constant angular velocity ω about a vertical axis passing through one of its ends. The tube contains carbon dioxide at a temperature T=300K. The length of the tube is l=100cm. Find the value ω at which the ratio of molecular concentrations at the opposite ends of the tube is equal to η=2.0.
View SolutionA horizontally oriented uniform rod AB of mass m=1.40kg and length l0=100cm rotates freely about a stationary vertical axis OO′ passing through its end A. The point A is located at the middle of the axis OO′ whose length is equal to l=55cm. At what angular velocity of the rod the horizontal component of the force acting on the lower end of the axis OO′ is equal to zero? What is in this case the horizontal component of the force acting on the upper end of the axis?
View SolutionA thin uniform copper rod of length l and mass m rotates uniformly with an angular velocity ω in a horizontal plane about a vertical axis passing through one of its ends. Determine the tension in the rod as a function of the distance r from the rotation axis. Find the elongation of the rod.
View Solution

