A particle P is to be projected from a fixed point A on the ground with a fixed speed u. Another particle Q is also to be projected from a point B which is directly above the point A. The trajectory of the particle Q touches all possible trajectories (for different angle of projection) of the particle P in the vertical x−y plane. Find the equation of trajectory of the particle Q. (Take the point A as origin, horizontal axis x− axis and vertical axis y−axis Consider the figure.)

In order for the trahectory of Q to touch that of P when the latter is projected vertically upward, Q must be projected horizontally from the highest point. To visualize this, consider the trajectories of P as the angle of projection of P(θ,say), approaches 90∘ (i.e. for vertical projection).Let Q be projected horizontally from B with a speed v, where A=u32g. The point of impact of Q on the horizontal plane represents the point of maximum range for P along the horizontal.
OC=u2g=v√2hg, where h=u22g
i.e., v=u
The trajectory of Q is
u22g−y=12gt2. where t=x/v(v≡u)

Topper's Solved these Questions
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Objective problems
215 Videos
- GMP ASSESMENTBOOK - FIITJEECHAPTER - GMP ASSESMENTEXERCISE - Assertion & Reason
15 Videos
- GENERAL PHYSICSBOOK - FIITJEECHAPTER - GENERAL PHYSICSEXERCISE - MATRIX MATCH TYPE
3 Videos
- GRAVITATIONBOOK - FIITJEECHAPTER - GRAVITATIONEXERCISE - Numerical based Question
2 Videos
Similar Questions
Knowledge Check
A particle is projected vertically upward with velocity u from a point A, when it returns to the point of projection .
AIts average speed is u/2.BIts average velocity is zero.CIts displacement is zero.DIts average speed is u.A particle is projected from point A on the ground at an angle θ with horizontal. Another particle is projected from point B simultaneously from height 4H above point A with same velocity A and B are in the same vertical plane, where H is the maximum height attained by the particle A, Both the particle collide at the same time on the ground. Find the angle at which particle B is projected with hoizontal.
Aθ upwardsBθ downwardsCzeroDNone of theseA particle is projected from the ground with an initial speed of v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
Av2√1+2cos2θBv2√1+2cos2θCv2√1+3cos2θDvcosθ
A particle is projected vertically upward with velocity u from a point A, when it returns to the point of projection .
View Solution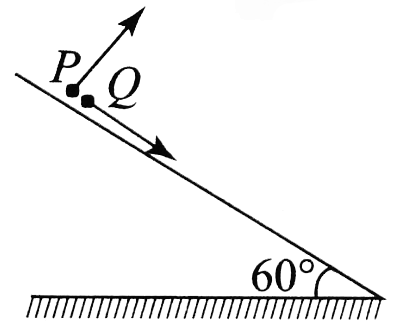
A particle P is projected from a point on the surface of smooth inclined plane (see figure). Simultaneously another particle Q is released on the smooth inclined plane from the same position. P and Q collide aftert=4. The speed of projection of P is
View Solution
A particle P is projected from a point on the surface of smooth inclined plane (see figure). Simultaneously another particle Q is released on the smooth inclined plane from the same position. P and Q collide aftert=4. The speed of projection of P is
View SolutionA particle is projected with a velocity →v=aˆi+bˆj. Find the radius of curvature of the trajectory of the particle at the (f) point of projection (ii) highest point.
View Solution
A particle P is projected from a point on the surface of smooth inclined plane (see figure). Simultaneously another particle Q is released on the smooth inclined plane from the same position. P and Q collide aftert=4. The speed of projection of P is
View Solution
