Question

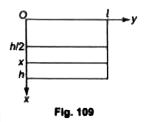
A rectangular vessel is filled with water and oil in equal proportion (by volume), the oil being twice lighter than water. Show that the force on ach side wall of the vessel will be reduced by one fifth it the vessel is filled only with oil. (Assume atmospheric pressrue is negligible)

Explanation

To solve the problem, we need to analyze the forces acting on the side walls of a rectangular vessel filled with water and oil in equal proportions. We will compare the force on the side walls when the vessel is filled with both fluids versus when it is filled only with oil.

1. Define the Variables:
- Let the density of oil be \( \rho \).
- Since oil is twice lighter than water, the density of water is \( 2\rho \).
- Let the height of the liquid column be \( h \).
- The area of each side wall of the vessel is \( A \).

2. Calculate the Pressure at Different Points:
- For a liquid column, the pressure at a depth \( h \) is given by \( P = \rho g h \).
- In the case of the vessel filled with both water and oil, the height of the oil column is \( \frac{h}{2} \) and the height of the water column is also \( \frac{h}{2} \).

3. Calculate Average Pressure on the Side Wall for Water and Oil:
- Oil:
- The pressure at the bottom of the oil column (depth \( \frac{h}{2} \)) is:
\( P_{\text{oil}} = \rho g \left(\frac{h}{2}\right) = \frac{\rho g h}{2} \)
- The average pressure due to oil is:
\( P_{\text{avg, oil}} = \frac{0 + \frac{\rho g h}{2}}{2} = \frac{\rho g h}{4} \)

- Water:
- The pressure at the bottom of the water column (depth \( h \)) is:
\( P_{\text{water}} = 2\rho g h \)
- The average pressure due to water is:
\( P_{\text{avg, water}} = \frac{0 + 2\rho g h}{2} = \rho g h \)

4. Calculate the Force on Each Side Wall:
- The force on the side wall due to oil and water combined is:
\( F_{\text{combined}} = P_{\text{avg, oil}} \cdot A + P_{\text{avg, water}} \cdot A = \left(\frac{\rho g h}{4} \cdot A + \rho g h \cdot A\right) \)
\( = \left(\frac{\rho g h}{4} + \rho g h\right) A = \left(\frac{\rho g h}{4} + \frac{4\rho g h}{4}\right) A = \frac{5\rho g h}{4} A \)

5. Calculate the Force on Each Side Wall When Filled Only with Oil:
- When the vessel is filled only with oil, the height of the oil column is \( h \):
\( P_{\text{only oil}} = \rho g h \)
- The average pressure is:
\( P_{\text{avg, oil only}} = \frac{0 + \rho g h}{2} = \frac{\rho g h}{2} \)
- The force on the side wall when filled only with oil is:
\( F_{\text{oil only}} = P_{\text{avg, oil only}} \cdot A = \left(\frac{\rho g h}{2}\right) A \)

6. Compare the Forces:
- The ratio of the forces when filled with both oil and water to when filled only with oil is:
\( \text{Ratio} = \frac{F_{\text{combined}}}{F_{\text{oil only}}} = \frac{\frac{5\rho g h}{4} A}{\frac{\rho g h}{2} A} = \frac{5/4}{1/2} = \frac{5}{2} \)
- Therefore, the force is reduced by:
\( \text{Reduction} = 1 - \frac{2}{5} = \frac{3}{5} \)
- This means the force on each side wall is reduced by one-fifth when the vessel is filled only with oil.