A cubical block of wood of 10cm and mass 0.92kg floats on a tank of water with oil or rel. density 0.6. Thickness of oil is 4cm above water. When the block attains equilibrium with four of its sides edges verical:
1cm of it will be above the free surface of oil.
5cm of it will be under water.
2cm of it will be above the common surface of oil and water.
8cm of it will be under water.
The correct Answer is:C, D
Assuming that the block is completely submerged in water, then
Fb=1000>mg(920) So, not possible
Let complete in oil
Fb=(0.6)(4)(1000+(1)(6)(100)=840
Fb<mg So, not possible
So, let 'x' part in oil and remaining in water
920=[(1)(10−x)+(0.6)(x)]100
9.2=10−x+0.6x
0.4x=0.8
x=2cm.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - IV10videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 3 PART - I17videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - FLUID MECHANICSEXERCISE - Exercise- 2 PART - II9videos
FLUID MECHANICS
- BOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise52videos
ELECTROSTATICS
- BOOK - RESONANCECHAPTER - FULL TEST 1EXERCISE - Exercise30videos
FULL TEST 1
Similar Questions
A piece of wood of relative density 0.25floats in a pail containing oil of relative density 0.81.What is the fraction of volume of the wood above the surface of the oil ?
View SolutionA cubical box of wood of side 30 cm weighting 21.6 kg floats on water with two faces horizontal. Calculate the depth of immersion of wood.
View Solution
Knowledge Check
- Question 1 - Select One or More
A cubical block of wood having an edge 10 cm and mass 0.92 kg floats on a tank of water with oil of relative density 0.5 to a height of 4 cm above water. When the block attains equilibrium with four of its edges vertical
A1 cm of it will be above the free surface of oilB5 cm of it will be under waterC1.6 cm of it will be above the comon surface of oil and waterD8.4 cm of it will be under water - Question 2 - Select One
A cubical box of wood of side 30 cm and mass 21.6 kg floats on water with two faces horizontal. The length of immersed part in water is :
(ρwood=0.8g/cc)A30 cmB12 cmC6 cmD24 cm - Question 3 - Select One
A cubical block of wood 10cm on a side, floats at the interface of oil and water as shown in figure. The density of oil is 0.6gcm−3 and density of water is 1gcm−3. The mass of the block is
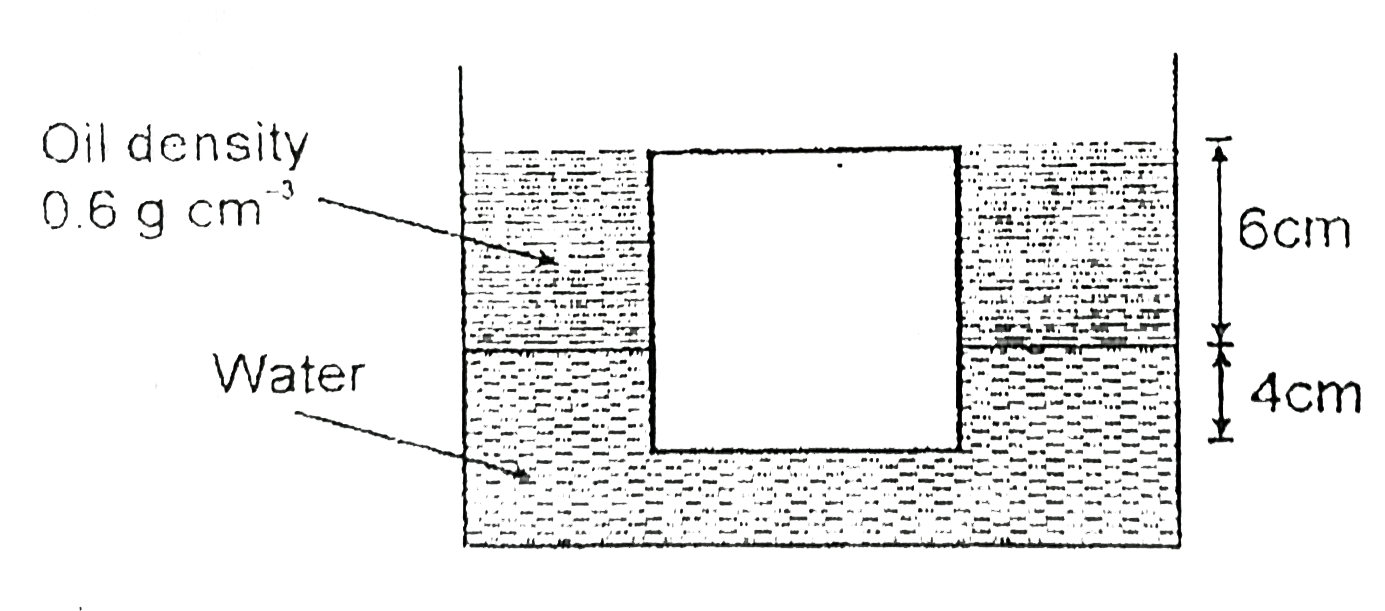 A706gB607gC760gD670g
A706gB607gC760gD670g
A block of wood floats in water with 23 of its volume submerged. Its relative density is
View SolutionA cubical block of wood 10 cm on a side floats at the interface between oil and water with its lower surface horizontal and 4 cm below the interface. The density of oil is 0.6gcm−3. The mass of block is
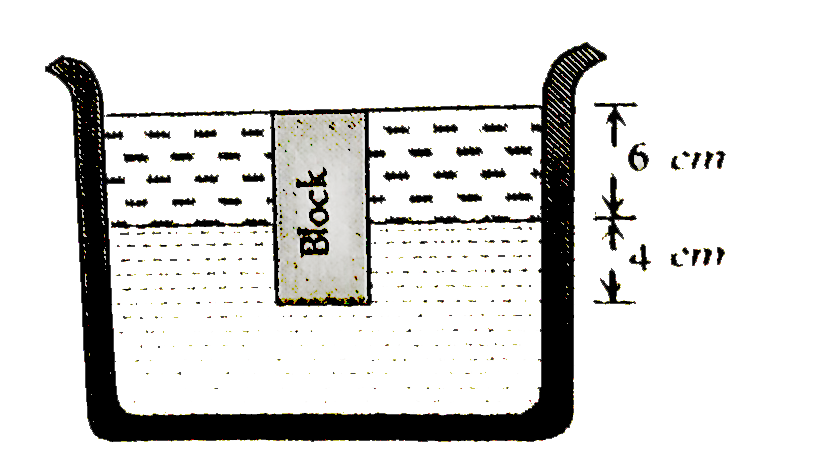 View Solution
View SolutionA cubical block of wood 10cm on a side floats at the interface between oil and water, as in fig. with its lower face 2cm below the interface. The intensity of the oli is 0.6gcm−3. The mass of the block is 1kg
 View Solution
View SolutionA cubical block is initially on water such that its 45th volume is submersed in water. Now oil is poured on water and when block attains equilibrium its half volume is in water and half volume is in oil. The relative density of oil is:
View SolutionThe densit of a block of wood which flots on water with 0.1 of its volume above water is:
View Solution

