A cubical box of wood of side 30 cm weighting 21.6 kg floats on water with two faces horizontal. Calculate the depth of immersion of wood.
For a floating body, the weight of displaced liquid should be equal to the weight of the block. Let x be the depth of immersion. Then
(x×30×30)×1×g=21.6×103×g
⇒x=21.6×103×g30×30×g=24cm
Topper's Solved these Questions
- BOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - QUESTIONS FOR PRACTICE6videos
HYDROSTATIC, FLUID MECHANICS & VISCOSITY
- BOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE-1 (OBJECTIVE PROBLEMS)100videos
HYDROSTATIC, FLUID MECHANICS & VISCOSITY
- BOOK - MOTIONCHAPTER - HEAT-2 EXERCISE - EXERCISE-4 (LEVEL-II)30videos
HEAT-2
- BOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 4 PREVIOUS YEAR (LEVEL 2)6videos
KINEMATICS
Similar Questions
A cubical block of wood of edge 3 cm floats in water. The lower surface of the cube just touches the free end of a vertical spring fixed at the bottom of the pot. Find the maximum weight that can be put on the block without wetting it. Density of wood =800kgm−3 and spring constant of the spring =50Nm−1Takeg=10ms−2.
 ,View Solution
,View SolutionA force of 49 N is just sufficient to pull a block of wood weighing 10 kg on a rough horizontal surface. Calculate the coefficient of friction and angle of friction.
View Solution
Knowledge Check
- Question 1 - Select One
A cubical box of wood of side 30 cm and mass 21.6 kg floats on water with two faces horizontal. The length of immersed part in water is :
(ρwood=0.8g/cc)A30 cmB12 cmC6 cmD24 cm - Question 2 - Select One or More
A cubical block of wood having an edge 10 cm and mass 0.92 kg floats on a tank of water with oil of relative density 0.5 to a height of 4 cm above water. When the block attains equilibrium with four of its edges vertical
A1 cm of it will be above the free surface of oilB5 cm of it will be under waterC1.6 cm of it will be above the comon surface of oil and waterD8.4 cm of it will be under water - Question 3 - Select One
A cubical block of wood 10 cm on a side floats at the interface between oil and water with its lower surface horizontal and 4 cm below the interface. The density of oil is 0.6gcm−3. The mass of block is
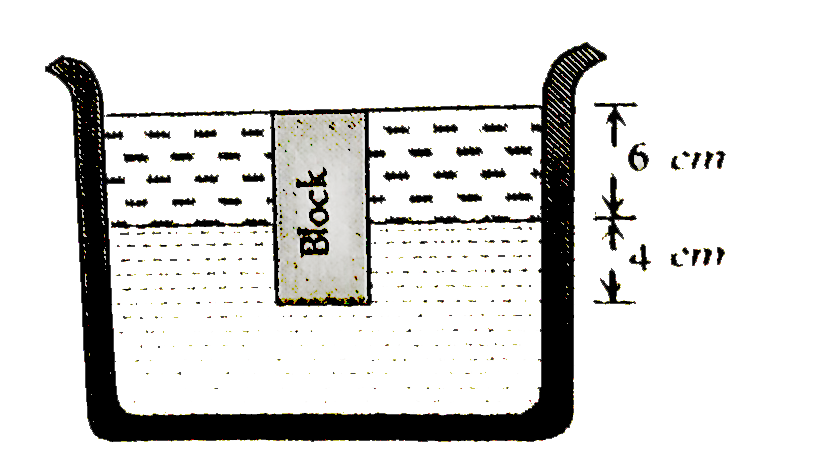 A706gB607gC760gD760g
A706gB607gC760gD760g
A cubical block of wood of side 5 cm is placed on a table. Find the thrust by the block wood on the table, if density of wood is 5gcm−3 and g is 10 ms−2.
View SolutionA cubical block of wood of edge a and density ρ floats in water of density 2ρ. The lower surface of the cube just touches the free end of a mass less spring of force constant K fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
View SolutionA cubical block of wood of 10cm and mass 0.92kg floats on a tank of water with oil or rel. density 0.6. Thickness of oil is 4cm above water. When the block attains equilibrium with four of its sides edges verical:
View SolutionA cubical block of wood of specific gravity 0.5 and chunk of concrete of specific gravity 2.5 are fastened together the ratio of mass of wood to the mass of concrete which makes the combination to float with entire volume of the combination submerged in water is
View SolutionA cubical block of side 0.5 m floats on water with 30% of its volume under water. What is the maximum weight that can be put on the block without fully submerging it under water?
[Take, density of water =103kg/m3]View Solution

