A Pitot tube is shown in figure. Wind blows in the direction shown. Air at inlet is brought to rest, whereas its speed just outside of opening is unchanged. The tube contains mercury of density . Find the speed of wind respect to Pitot tube. Neglect the height difference between and and take the density of air as .
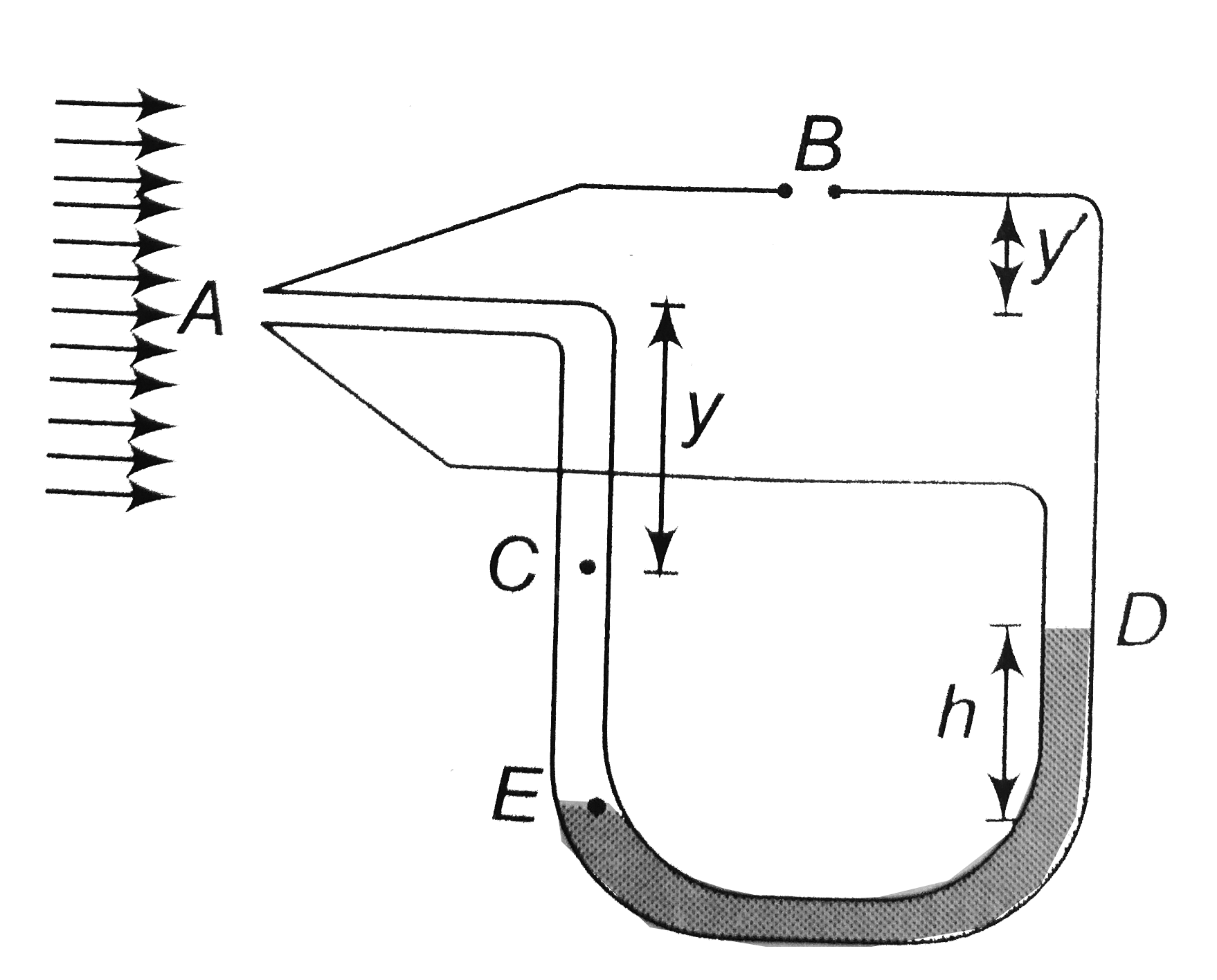
The correct Answer is:
Bernoulli's equation between and gives
Also equating pressures at horizontal level of
.
.
Topper's Solved these Questions
Similar Questions
Figure shows a device called Pitot tube . It measures the velocity of moving fluids . Determine the velocity of the fluid in terms of the density ρ the density of the fluid in manometer (U-tube) σ and the height h .
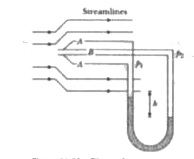 View Solution
View SolutionA Pitot tube (figure) is mounted along the axis of a gas pipeline whose cross-sectional area is equal to S. Assuming the viscosity to be negligible, find the volume of gas flowing across the section of the pipe per unit time, if the difference in the liquid columns is equal to Δh, and the densities of the liquid and the gas are ρ0 and ρ respectively.
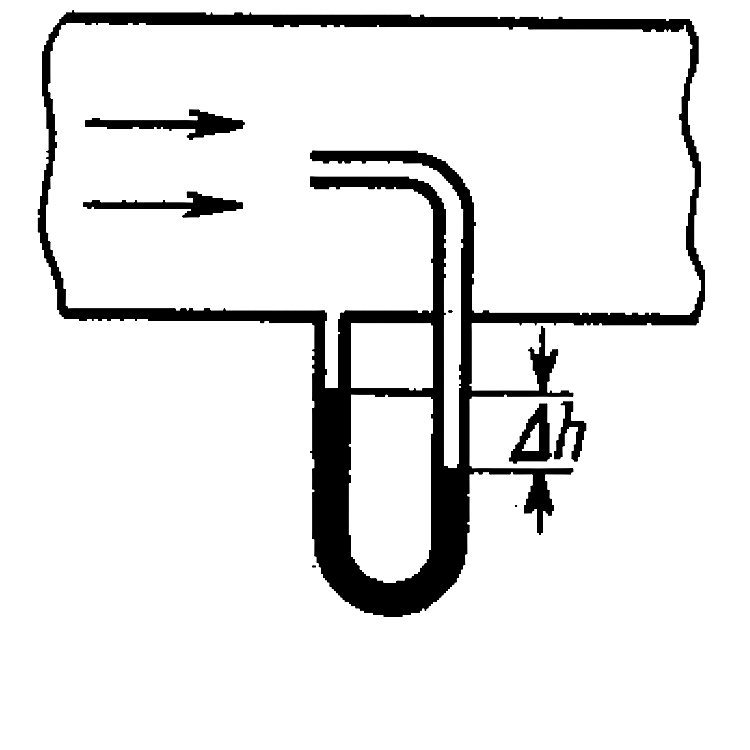 View Solution
View Solution
Knowledge Check
- Question 1 - Select One

A sealed tank containing a liquid of density ρ moves with a horizontal acceleration a, as shown in the figure. The difference in pressure between the points A and B isAhρgBlρaChρg−lρaDhρg+lρa - Question 2 - Select One
A sealed tank containing a liquid of density ρ moves with horizontal acceleration a as shown in the figure. The difference in pressure between two points A and B will be
 AhρgBlρgChρg−lρaDhρg−lρa
AhρgBlρgChρg−lρaDhρg−lρa - Question 3 - Select One
A spray gun is shown in the figure where a piston pushes air out of a nozzle. A thin tube of uniform cross section is connected to the nozzle. The other end of the tube is in a small liquid container. As the piston pushes air through the nozzle, the liquid from the container rises into the nozzle and is sprayed out. For the spray gun shown, the radii of the piston and the nozzle are 20mm and 1mm respectively. The upper end of the container is open to the atmosphere.
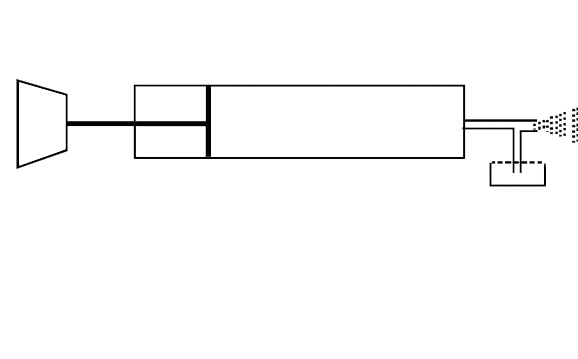
If the density of air is ρa, and that of the liquid ρl, then for a given piston speed the rate (volume per unit time) at which the liquid is sprayed will be proportional toA(a) √ρaρlB(b) √ρaρlC(c) √ρlρaD(d) ρl
Two capillaries of small cross section are connected as shown in the figure. The right tube has cross sectional radius R and left one has a radius of r(<R). The tube of radius R is very long where as the tube of radius r is of short length. Water is slowly poured in the right tube. Contact angle for the tube wall and water is θ=0∘. Let h be the height difference between water surface in the right and left tube. Surface tension of water is T and its density is ρ.
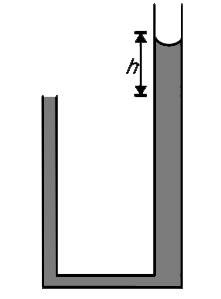
(a) Find the value of h if the water surface in the left tube is found to be flat.
(b) Find the maximum value of h for which water will not flow out of the left tube .View SolutionWhen a capillary tube of radius r is dipped vertically in a liquid of surface tension T, the liquid rises to a height h in the tube above the level outside the tube . If the angle of contact is θ the density of the liquid is ρ then the pressure difference between the points A and B is
 View Solution
View SolutionA point tube is mounted on an aeroplane wing to measure the speed of the plane. The tube contains alcohol and shows a level difference of 40 cm. What is the speed of the plane reative to air ? (sp. Gr. Of alcohol = 0.8 and density of air = 1 kg m−3).
View SolutionA U-tube of base length l filled with the same volume of two liquids of densities ρ and 2ρ is moving with an acceleration 'a' on the horizontal plane. If the height difference between the two surfaces (open to atmosphere) becomes zero, then the height h is given by
 View Solution
View SolutionFigure shows as thin tube open at one end rotating with constant angular speed ω. The other end of the tube has a small opening. Tube contains a fluid of density ρ which effuses with speed u relative to the tube. Let ρA be the pressure at the point in the tube just behind the opening. Assume the atmospheric pressure to be p0 and pick correct option(s) for the instant when h=l2
 View Solution
View Solution

