The linear mass density of a ladder of length $l$ increases uniformly from one end $A$ to the other end $B$ ,
(a) Form an expression for linear mass density as function of distance $x$ from end $A$ where linear mass density $λ_{0}$ . The density at one end being twice that of the other end.
(b) find the position of the centre of mass from end $A$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:(a) $λ (x) = λ_{0} + \frac{λ_{0} x}{L}$ , (b) $\frac{5}{9} L$

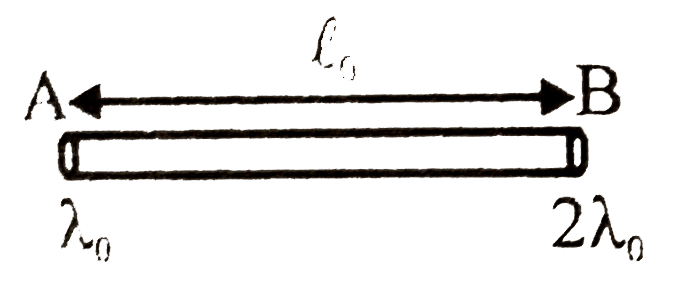
(a) $λ = Ax+B$
$λ_{A} = A (0) + B = B = λ_{0} [x = 0]$
$λ_{B} = A L + B = 2 λ_{0} \Rightarrow A = \frac{λ_{0}}{L}$
$\Rightarrow λ = \frac{λ_{0}}{L} x + λ_{0}$
(b) $x_{C M} = \frac{\int (x) λ d x}{\int λ d x} = \frac{\int_{0}^{L} (x) (\frac{λ_{0}}{L} x + λ_{0}) d x}{\int_{0}^{L} (\frac{λ_{0}}{L} x + λ_{0}) d x} = \frac{\frac{L^{2}}{3} + \frac{L^{2}}{2}}{\frac{L}{2} + L} = \frac{\frac{5 L^{2}}{6}}{\frac{3 L}{2}} = \frac{5}{9} L$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The linear mass density $' μ'$ of the string is (where, mass of the string = m, length of the string = L)
A $\frac{m}{L}$
BmL
C $m t^{2}$
D $\frac{m}{L_{3}}$
Question 2 - Select One
The linear mass density $μ$ of the string is (where, mass of the string = m, length, of the string g = L)
A $\frac{m}{L}$
BmL
C $m L^{2}$
D $\frac{m}{L_{3}}$
Question 3 - Select One
Find centre of mass of given rod of linear mass density $λ = (a + b {(\frac{x}{l})}^{2})$ , x is distance from one of its end. Length of the rod is $l$ .
A $\frac{3 l}{4} (\frac{3 a + b}{2 a + b})$
B $\frac{3 l}{4} (\frac{2 a + b}{3 a + b})$
C $\frac{l}{4} (\frac{2 a + b}{3 a + b})$
D $l (\frac{2 a + b}{3 a + b})$

BANSAL-CENTRE OF MASS & MOMENTUM CONSERVATION-EXERCISE-3 (Miscellaneous Exercise)

Home
Ask Doubt
Profile