Find the gravitational force of interaction between the mass m and an infinite rod of varying mass density λ such that λ(x)=kx, where x is the distance from mass m. Given that mass m is placed at a distance d from the of the rod on its axis as shown in figure. If force is Gmknd2 Fill n in OMR sheet.
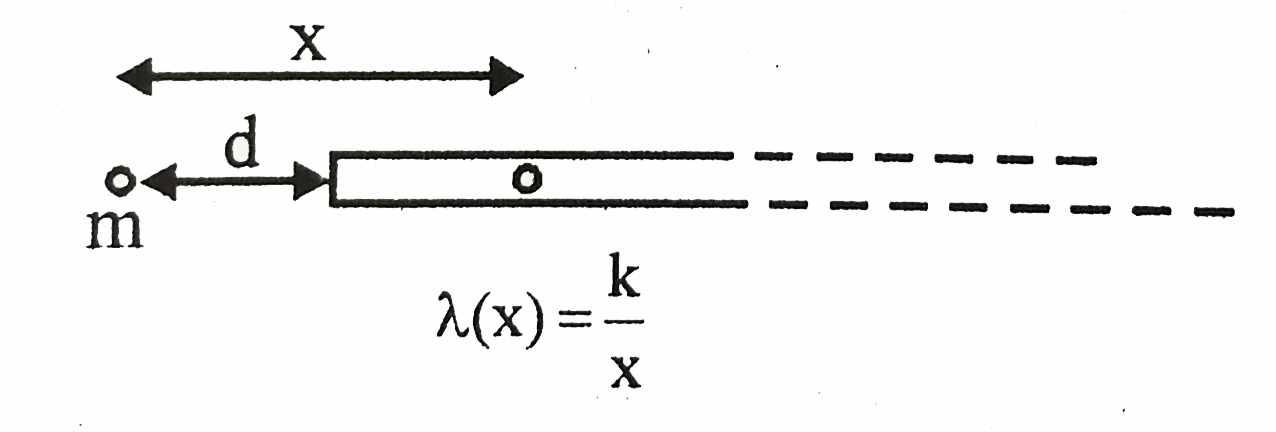
The correct Answer is:2
dF=Gmdmx2=Gmx2(Kx)dx
Integrate from d to ∞
F=GmK2d2
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - A16videos
GRAVITATION
- BOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - B6videos
GRAVITATION
- BOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -2 [Matrix Type]1videos
GRAVITATION
- BOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-B) (JEE-ADVANCED Previous Year Questions)8videos
CENTRE OF MASS & MOMENTUM CONSERVATION
- BOOK - BANSALCHAPTER - HEAT TRANSFEREXERCISE - Exercise89videos
HEAT TRANSFER
Similar Questions
Find the gravitational force between a point like mass M and an infinitely long, thin rod, of mass density ρ, which is at a distance L from the mass M.
View Solutionfind the gravitational force of attraction between a uniform sphere of mass M and a uniform rod of length L and mass m, placed such that r is the distance between the centre of the sphere and the near end of the road.
View Solution
Knowledge Check
- Question 1 - Select One
The gravitational force of attraction between a uniform sphere of mass M and a uniform rod of length l and mass in as shown in figure is
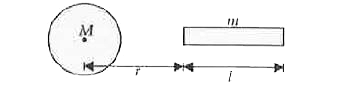 AGMmr(r+1)BGMr2CMm2D(r2+1)mM
AGMmr(r+1)BGMr2CMm2D(r2+1)mM - Question 2 - Select One
A mass m is placed inside a hollow sphere of mass M as shown in figure. The gravitaional force on mass m is
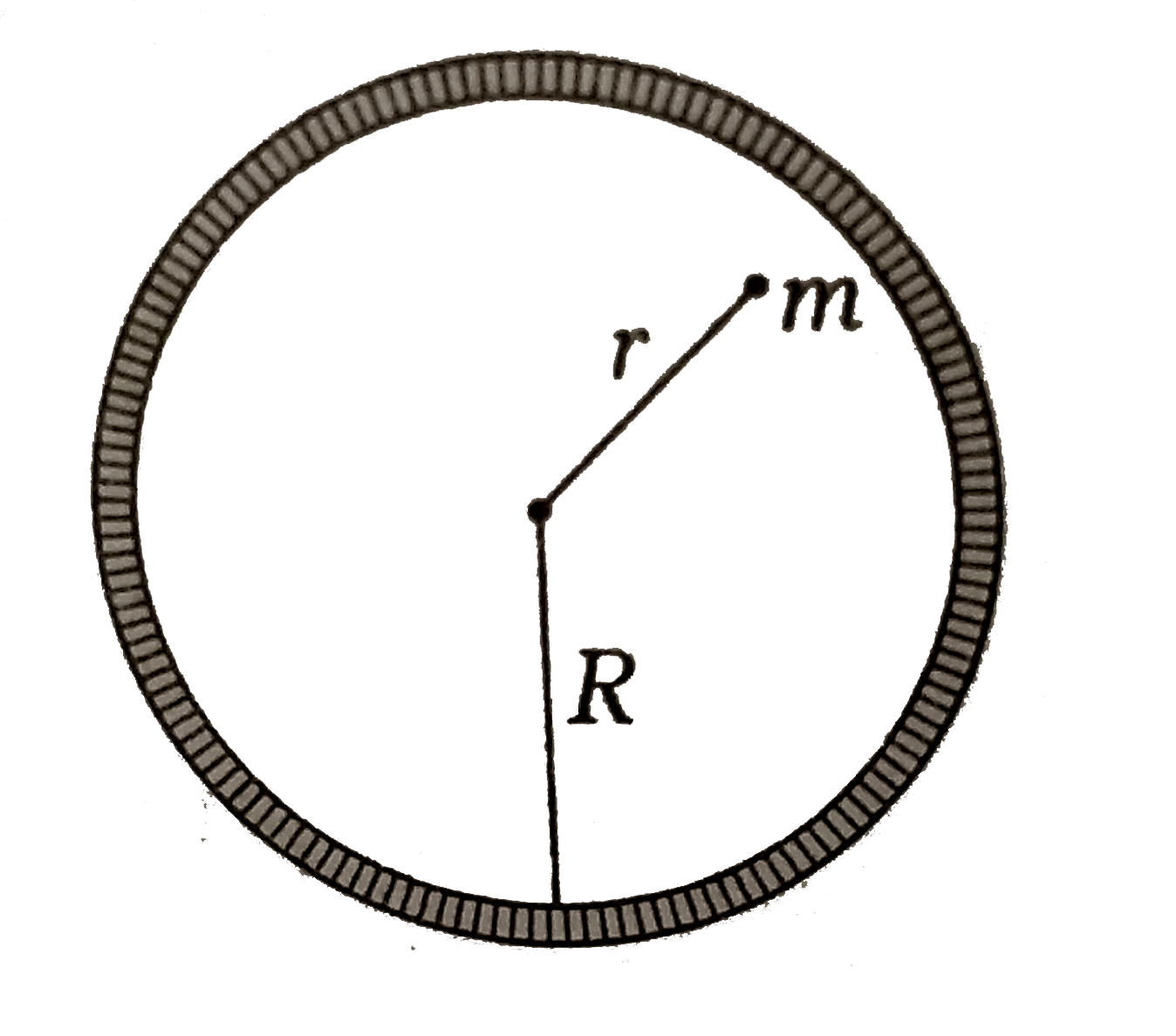 AGMmR2BGMmr2CGMm(R−r)2Dzero
AGMmR2BGMmr2CGMm(R−r)2Dzero - Question 3 - Select One
A mass m is placed in the cavity inside hollow sphere of mass M as shown in the figure. The gravitational force on m is
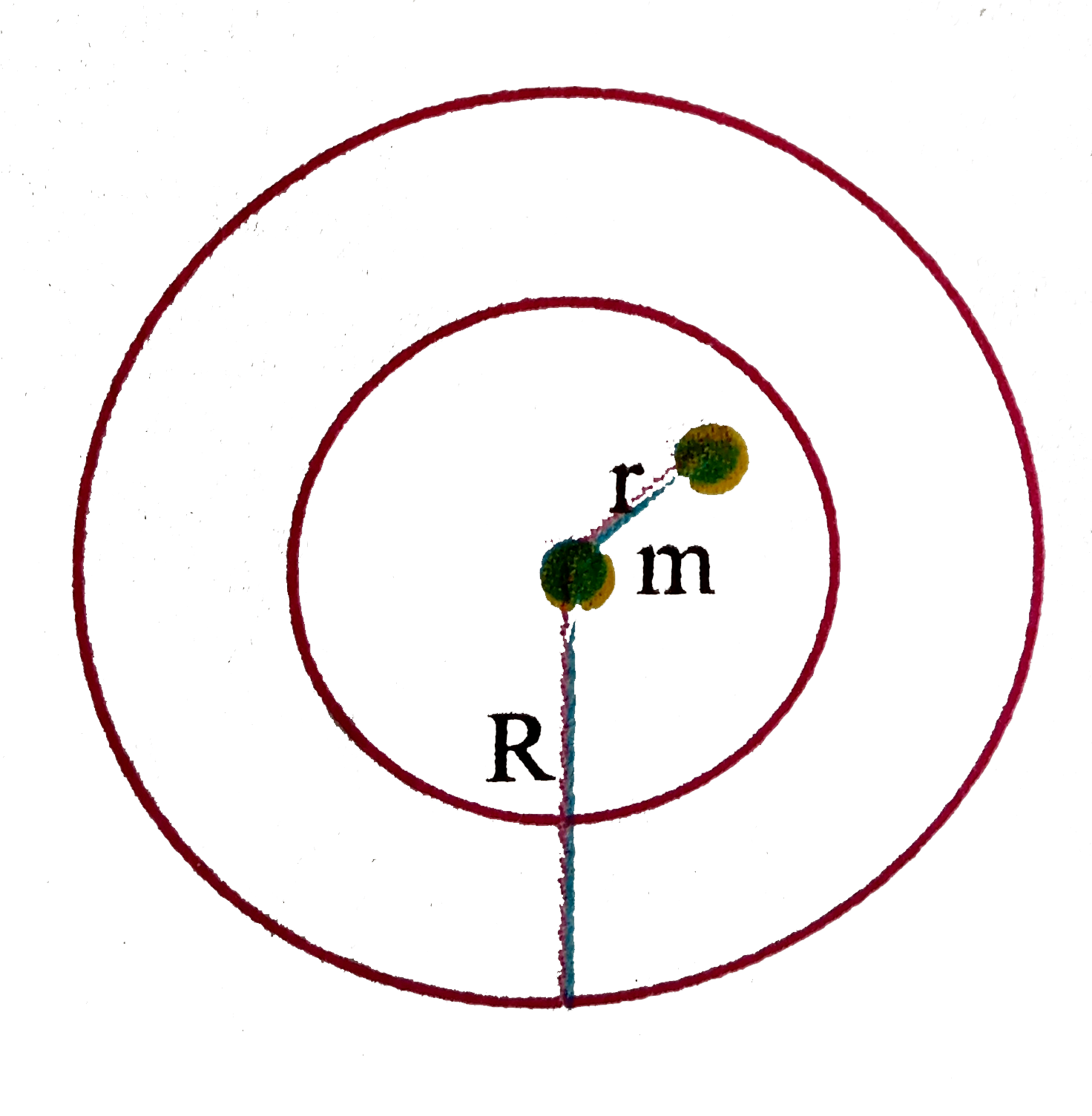 AGMmR2BGMmr2CGMm(R−r)2Dzero
AGMmR2BGMmr2CGMm(R−r)2Dzero
Find coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View SolutionFind the gravitatinal force of between a point mass m placed at a disance x on the prolongation of a thin rod of mass M andlength l from near end .
View SolutionThe linear density of a thin rod of length 1m lies as λ=(1+2x), where x is the distance from its one end. Find the distance of its center of mass from this end.
View SolutionFind the gravitational interaction energy of system consisting of a disc of mass M, radius R and a small mass m dituated at a distance x from disc centre on its axis as shown in figure.
 View Solution
View SolutionFind centre of mass of given rod of linear mass density λ=(a+b(xl)2) , x is distance from one of its end. Length of the rod is l.
View Solution

