The spectral emissive power for a body at temperature is poltted againist the wavelenght and area under the curve is found to be a different temperature the area is found to be A then
 .
.
Topper's Solved these Questions
Similar Questions
A black body emits maximum radiation of wavelength λ1 at a certain temperature T1. On increasing the temperature, the total energy of radiation emitted is increased 16 times at temperature T2. If λ2 is the wavelength corresponding to which maximum radiation is emitted at temperature T2. Calculate the value of (λ1λ2).
View SolutionA black body emits maximum radiation of wavelength λ1=2000 Å at a certain temperature T1. On increasing the temperature , the total energy of radiation emitted is increased 16 times at temperature T2. If λ2 is the wavelength corresponding to which maximum radiation emitted at temperature T2. Calculate the value of (λ1λ2)
View Solution
Knowledge Check
- Question 1 - Select One
The spectral emissive power Eλ for a body at temperature T1 is plotted against the wavelength and area under the curve is found to be 9A.At a different temperature T2 the area is found to be A then λ1/λ2=
 .A3B13C1√3D√3
.A3B13C1√3D√3 - Question 2 - Select One
The ratio of spectral emissive power of a body λ and temperature T is equal to a physical quantity at the wavelength and temperature. Then the physical quantity is
Aemissive power of the bodyBabsorptive powe of the bodyCreflective power of the bodyDtransmission coefficient of the body - Question 3 - Select One
The spectral emissive power of a black body at a temperature of 6000K is maximum at λm=5000Å. If the temperature is increased by 10%, then the decrease in λm will be -
A2.5%B5.0%C7.5%D10%
A black body emits maximum radiation of wavelength is λ1= 2000 Å at a certain temperature T1. On increasing the temperature, the total energy of radiation emitted is increased 16 times at temperature T2 .If λ2 is the wavelength corresponding to which maximum radiation emitted at temperature T2 Calculate the value of (λ1λ2)
View SolutionIf for a black body the graph of change is emissive power at different temperatures T1,T2andT3 with wavelength is according to the figure then –
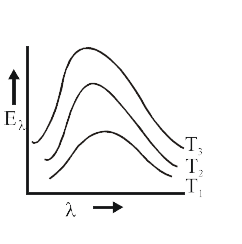 View Solution
View SolutionLet the wavelength at which the the spectral emissive power of a black body (at a temperature T) is maximum, be denoted by λmax as the temperature of the body is increased by 1K, λmax decreases by 1 percent. The temperature T of the black body is
View SolutionThe adjoining diagram shows the spectral energy density distribution Eλ of a black body at two different temperatures. If the areas under the curves are in the ratio 16 : 1, the value of temperature T is
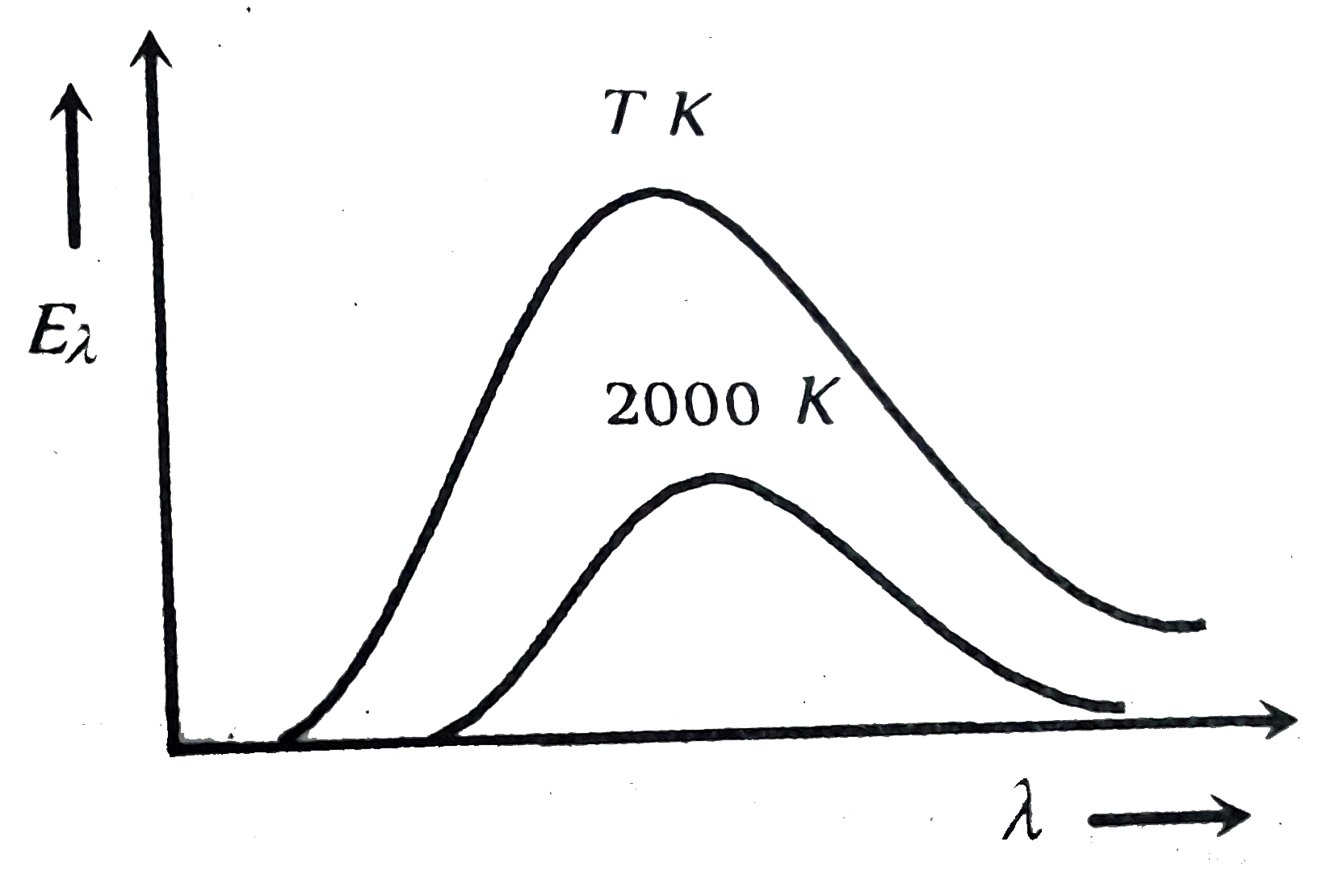 View Solution
View SolutionIf λm denotes the wavelength at which the radiative emission from a black body at a temperature TK is maximum, then
View Solution

