A plumber steps out of his truck, walks 60m east and 35m south and then taken an elevator, 12m down to the basement of a building where a bad leak is occurring. Assume x axis is east , y-exis is north and z-axis us up, Find displacement of plumber in term of conventional co-ordinate system ?
The correct Answer is:60ˆi−35ˆj−12ˆk
To find the displacement of the plumber in terms of the conventional coordinate system, we can break down the problem step by step.
Step 1: Define the Coordinate System
- The x-axis represents the east direction.
- The y-axis represents the north direction.
- The z-axis represents the vertical direction, where positive z is up and negative z is down.
Step 2: Determine the Movements
1. The plumber walks 60 meters east:
- In terms of coordinates, this is represented as +60^i.
2. Then, he walks 35 meters south:
- South is in the negative y direction, so this is represented as −35^j.
3. Finally, he takes an elevator 12 meters down:
- Down is in the negative z direction, so this is represented as −12^k.
Step 3: Combine the Displacements
Now we can combine these movements into a single displacement vector →D:
→D=60^i−35^j−12^k
Final Displacement Vector
Thus, the displacement of the plumber in terms of the conventional coordinate system is:
→D=60^i−35^j−12^k
---
- The x-axis represents the east direction.
- The y-axis represents the north direction.
- The z-axis represents the vertical direction, where positive z is up and negative z is down.
1. The plumber walks 60 meters east:
- In terms of coordinates, this is represented as +60^i.
2. Then, he walks 35 meters south:
- South is in the negative y direction, so this is represented as −35^j.
3. Finally, he takes an elevator 12 meters down:
- Down is in the negative z direction, so this is represented as −12^k.
Now we can combine these movements into a single displacement vector →D:
→D=60^i−35^j−12^k
Thus, the displacement of the plumber in terms of the conventional coordinate system is:
→D=60^i−35^j−12^k
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - UNIT DIMENSION, VECTOR & BASIC MATHSEXERCISE - Exercise10videos
UNIT DIMENSION, VECTOR & BASIC MATHS
- BOOK - BANSALCHAPTER - UNIT DIMENSION, VECTOR & BASIC MATHSEXERCISE - EXERCISE - 2 [MATRIX TYPE]1videos
UNIT DIMENSION, VECTOR & BASIC MATHS
- BOOK - BANSALCHAPTER - KINETIC THEORY OF GASESEXERCISE - Section-B13videos
KINETIC THEORY OF GASES
Similar Questions
A truck is travelling due north descending a hill of slope angle θ=tan–1(0.1) at a constant speed of 90km/hr. At the base of the hill there is a gentle curve and beyond that the road is level and heads 30∘ east of north. A south bound police car is travelling at 80km/hr along the level road at the base of the hill approaching the truck. Find the velocity of the truck relative to police car in terms of unit vectors ˆi,ˆj and ˆk . Take x axis towards east, y axis towards north and z axis vertically upwards.
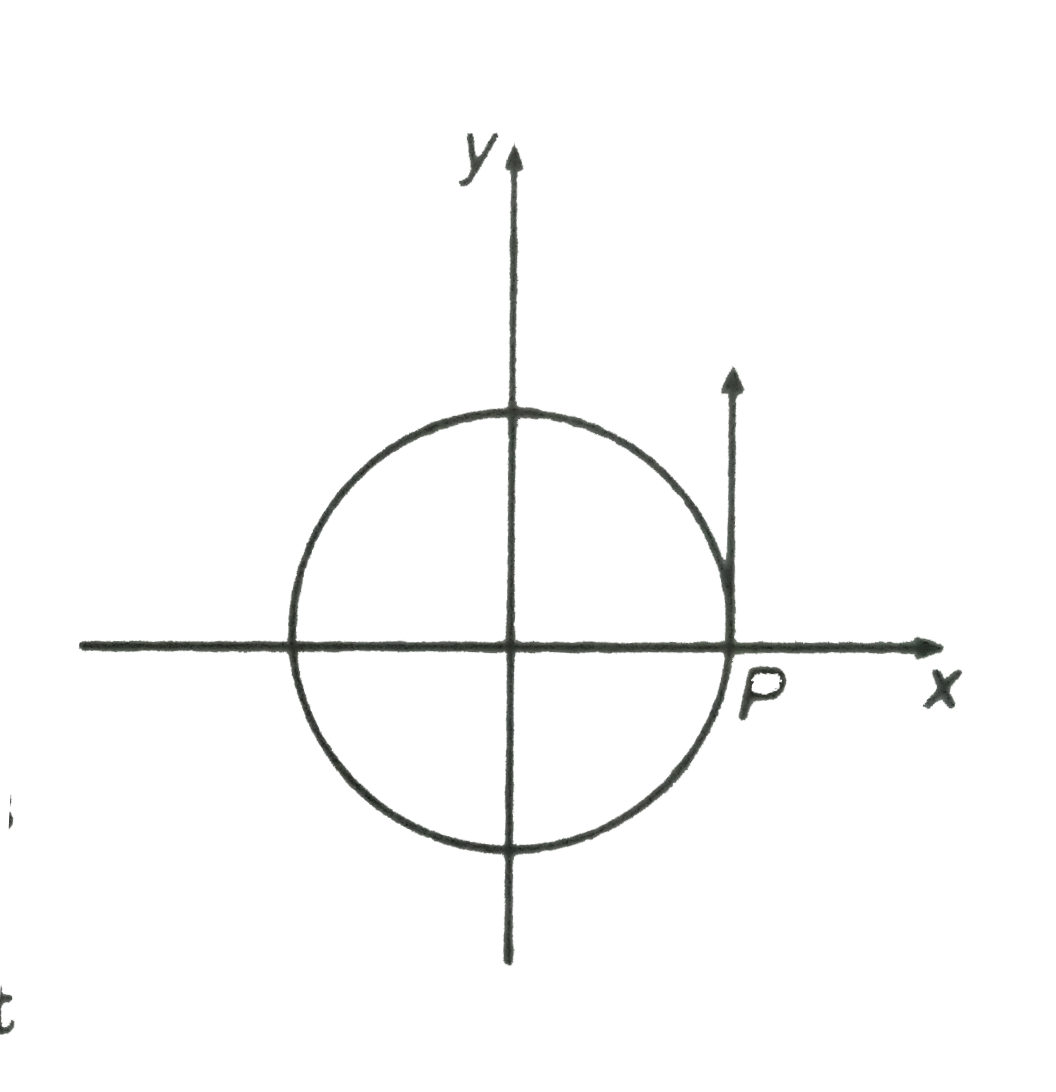
View SolutionA train is moving with a constant speed of 10m/s in a circle of radius 16πm. The plane of the circle lies in horizontal x-y plane. At time t = 0, train is at point P and moving in counter- clockwise direction. At this instant, a stone is thrown from the train with speed 10m/s relative to train towards negative x-axis at an angle of 37∘ with vertical z-axis . Find
(a) the velocity of particle relative to train at the highest point of its
trajectory.
(b) the co-ordinates of points on the ground where it finally falls and that of the hightest point of its trajectory. (Take g =10m/s2,sin37∘=35
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A plumber steps down 1 m out of his truck and walks 50m east and then 25m South, and then takes an elevator to the basement of the building 9 m below steet level. If the east, the north and the upwards direction are represent by the positive x, y and z- axes, which one of the following represent displacement (meters ) of the plumber ?
A50ˆi−25ˆj−9ˆkB50ˆi+25ˆj−9ˆkC50ˆi−25ˆj−10ˆkD50ˆi+25ˆj−10ˆk - Question 2 - Select One
Consider east as positive x-axis, north as positive y-axis. A girl walks 10m east first time than 10m in a direction 30∘ west of north for the second time and then third time in unknown direction and magnitude so as to return to her initial position. What is her third displacement in unit vector notation.?
A−5ˆi−5√3ˆjB5ˆi−5√3ˆjC−5ˆi+5√3ˆjDShe cannot return - Question 3 - Select One
A car moves 40 m due east and turns towards north and moves 30 m then tursn 45∘ east of norht and moves 20√2m. The net displacment of car is (east is taken positive x-axis, North as positive y-axis)
A50ˆi+60ˆjB60ˆi+50ˆjC30ˆi+40ˆjD40ˆj+30ˆj
A body constrained to move along the Y-axis of a co-ordinate system is subjected to a constant force →F given unit →F=−ˆi+6ˆj+2ˆk newton where ˆi,ˆjandˆk represent unit vector along X-, Y- and Z-axis of the system , respectively . Calculate the work done by the force in displacement the body through a distance of 4 m along the Y-axis .
View Solution(a) A charge particle travelling along positive x direction with speed Vx enters a region of width having a uniform electric field E in positive y direction. A screen is kept, at a distance D(>>l) from the region of the field, in yz plane. Find the y co-ordinate of the point where the particle strikes the screen. Charge and mass of the par- ticle is + q and m respectively.
(b) The electric field in the region is replaced with a uniform magnetic field B in negative z direction. Now calculate the y co-ordinate of the point on the screen where the particle hits it. Assume deflection due to field to be small and D>>l.
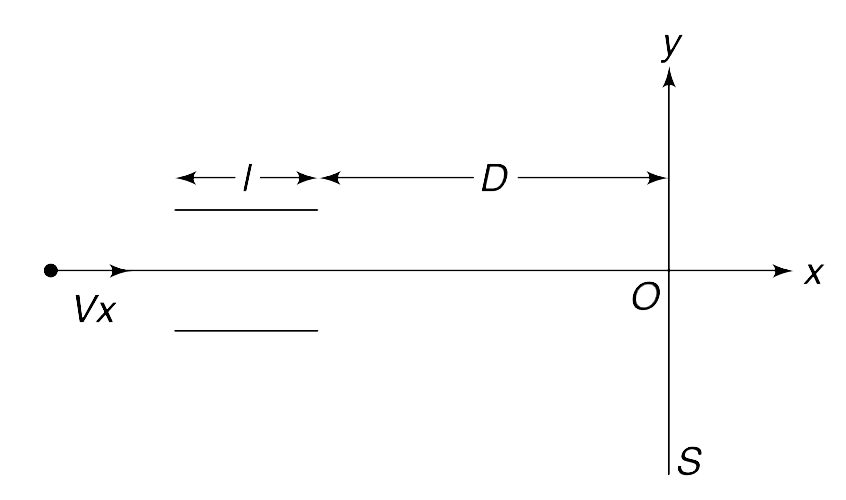
(c) Now the field region is filled with a uniform electric (E) and magnetic field (B) both directed in positive y direction. A beam of protons and some other positive ion enters the region trav- elling along x direction. The particles hit the screen along two curved paths. Explain. Draw the two curves in yz plane and point out which one represents the protons.View SolutionOne of the major requirement in atomic structure is determination of location of electron inside an atom. The wave mechanical model establishes this in accordance with Heisenberg's uncertainity principle through the concept of orbitals. The orbitals are defined as that '3D' space in which probability of finding electron is maximum and are represented by wave functions Ψn,l,m where n,l and m are quantum number. The variation of Ψ is analysed in terms of polar coordinates and hence Ψ=f(r,0,ϕ) where 'r' represents radius vector and 0 and ϕ represents angle (∠) Which the radius vector with x-axis respectively. The expressions of Ψr,0,ϕ are often given in terms of σ instead of r where σ=2Zrnα0 and Z = atomic number and n= shell number.
If an orbital is represented as:
Ψr,0,ϕ=23(13α0)3/2.(σ−1)(σ2−8σ+12)
.σ−σ/2.cos0
belong to which orbital?View SolutionX and Y are two children playing a game. They start from the same point. X walks 11 m North, then turns to his right and walks 21 m. At the same time, Y walks 11 m East, then turns South and walks 5 m, then turns to his left and walks 10 m. Where is Y now with respect to the position of X?
View SolutionLet us consider a diatomic gas whose molecules have the shape of a dumbell. In this model, the center of mass of the molecule can translate in the x,y and z directions. In addition, the molecule can rotate about three mutually perpendicular axes. We can neglect the rotation about the y -axis because the moment of inertia Iy and the rotational energy 12Iyω2 about this axis are negligible compared with those associated with the x and z axes. (If the two atoms are taken to the point masses, then Iy is identically zero). Thus, there are five degrees of freedom: three associated with the translation motion and two associated with the rotational motion. Because each degree of freedom contributes, on average, 12kBT of energy per molecule, the total internal energy for a system of N molecules is:
Eint=3N(12kBT)+2N(12kBT)=52NKBT=52nRT...........(i)
We can use this result to find the molar specific heat at constant volume:
Cv=1ndEintdT=1nddT(52nRT)=52R................(ii)
From equation (i) and (ii) we find that
CP=CV+R=72R
γ=CPCV=7/2R5/2r=75=1.40
In the vibratory model, the two atoms are joined by an imaginary spring. The vibrational motion adds two more degrees of freedom, which correspond to the kinetic energy and the potential associated with vibrations along the length of the molecule about its centre of mass.

The root mean square angular velocity of a diatomic molecule (with each atom of mass m andn interatomic distance a) is given by:View Solution

