Let us consider a diatomic gas whose molecules have the shape of a dumbell. In this model, the center of mass of the molecule can translate in the x,y and z directions. In addition, the molecule can rotate about three mutually perpendicular axes. We can neglect the rotation about the y -axis because the moment of inertia Iy and the rotational energy 12Iyω2 about this axis are negligible compared with those associated with the x and z axes. (If the two atoms are taken to the point masses, then Iy is identically zero). Thus, there are five degrees of freedom: three associated with the translation motion and two associated with the rotational motion. Because each degree of freedom contributes, on average, 12kBT of energy per molecule, the total internal energy for a system of N molecules is:
Eint=3N(12kBT)+2N(12kBT)=52NKBT=52nRT...........(i)
We can use this result to find the molar specific heat at constant volume:
Cv=1ndEintdT=1nddT(52nRT)=52R................(ii)
From equation (i) and (ii) we find that
CP=CV+R=72R
γ=CPCV=7/2R5/2r=75=1.40
In the vibratory model, the two atoms are joined by an imaginary spring. The vibrational motion adds two more degrees of freedom, which correspond to the kinetic energy and the potential associated with vibrations along the length of the molecule about its centre of mass.

The root mean square angular velocity of a diatomic molecule (with each atom of mass m andn interatomic distance a) is given by:
√mkBTma2
√2kBTma2
√kBTma2
√kBT2ma2
The correct Answer is:B
12Ixω2+12Iyω2=f2kT{ffractional=2}
Ix=Iy⇒μr2=m2a2{μ=m1m2m1+m2}
ma22ω2=22klTμ=m2
ω=√2KTma2
Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
The axis X and Z in the plane of a disc are mutually perpendicular and Y-axis is perpendicular to the plane of the disc. If the moment of inertia of the body about X and Y axes is respectively 30 kg m2 and 40 kg m2 then M.I. about Z-axis in kg m2 will be:
View SolutionA round disc of moment of inertia I2 about its axis perpendicular to its plane and passing through its centre is placed over another disc of moment of inertia I1 rotating with an angular velocity ω about the same axis. The final angular velocity of the combination of discs is.
View Solution
Knowledge Check
Let us consider a diatomic gas whose molecules have the shape of a dumbell. In this model, the center of mass of the molecule can translate in the x,y and z directions. In addition, the molecule can rotate about three mutually perpendicular axes. We can neglect the rotation about the y -axis because the moment of inertia Iy and the rotational energy 12Iyω2 about this axis are negligible compared with those associated with the x and z axes. (If the two atoms are taken to the point masses, then Iy is identically zero). Thus, there are five degrees of freedom: three associated with the translation motion and two associated with the rotational motion. Because each degree of freedom contributes, on average, 12kBT of energy per molecule, the total internal energy for a system of N molecules is:
Eint=3N(12kBT)+2N(12kBT)=52NKBT=52nRT...........(i)
We can use this result to find the molar specific heat at constant volume:
Cv=1ndEintdT=1nddT(52nRT)=52R................(ii)
From equation (i) and (ii) we find that
CP=CV+R=72R
γ=CPCV=7/2R5/2r=75=1.40
In the vibratory model, the two atoms are joined by an imaginary spring. The vibrational motion adds two more degrees of freedom, which correspond to the kinetic energy and the potential associated with vibrations along the length of the molecule about its centre of mass.

A diatomic molecule is moving without rotation or vibration with velocity vrms such that it is oriented along x- axis. It strikes a wall in yz- plane while moving in +ve x direction. The spring constant can be assumed to be K and time of collision is negligible. After all collision are over:AThe molecule is moving along -ve x-direction and oscillating about its centre of massBThe molecule is moving along -ve x-direction but not oscillating about its centre of massCThe molecule is oscillating about it centre of mass but not moving at allDThe molecule is neither rotating nor moving at allA rod AB of mass m and length l is rotating about a vertical axis as shown. It's moment of inertia about this axis is :
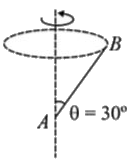 Aml23Bml24Cml216Dml212
Aml23Bml24Cml216Dml212The axis X and Z in the plane of a disc are mutually perpendicular and Y-axis is perpendicular to the plane of the disc. If the moment of inertia of the body about X and Y axes is respectively 30 kg m2 and 40 kg m2 then M.I. about Z-axis in kg m2 will be:
A70B50C10DZero
Show that the moment of inertia of a body about the given axis of rotation is equal to twice the kinetic energy of rotation of the body rotating with unit angular velocity
View SolutionThe figure shows three small spheres that rotate about a vertical axis. The perpendicular distance between the axis and the center of each sphere is given. Rank the three spheres according to their rotational inertia about that axis, greatest first.
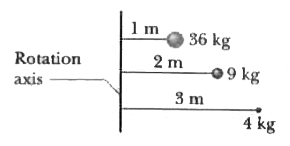
View SolutionThe kinetic energy of an object rotating about a fixed axis with angular momentum L=Iω can be written as.
View SolutionA round disc of moment of inertia I2 about its axis perpendicular to its plane and passing through its centre is placed over another disc of moment of inertia I1 rotating with an angular velocity ω about the same axis. The final angular velocity of the combination of discs is.
View SolutionIf the kinetic energy of rotation of a body about an axis is 9 J and the moment of inertia is 2 kg m2, then the angular velocity of the body about the axis of rotation in rad/s is
View Solution
