A charge q moves in a region where electric field E and the magnetic field B both exist, then the force on its is
The correct Answer is:B
To solve the problem of finding the force on a charge q moving in an electric field E and a magnetic field B, we can break it down into steps:
1. Identify the forces acting on the charge:
- The charge q experiences two types of forces: one due to the electric field and another due to the magnetic field.
2. Calculate the force due to the electric field:
- The force Fe on the charge due to the electric field E is given by the formula:
Fe=qE
- Here, q is the charge and E is the electric field strength.
3. Calculate the force due to the magnetic field:
- The force Fm on the charge moving with velocity v in a magnetic field B is given by the formula:
Fm=q(v×B)
- This is a vector product, meaning the direction of the force is determined by the right-hand rule, and v is the velocity of the charge.
4. Combine the forces:
- The net force F acting on the charge q is the sum of the electric force and the magnetic force:
F=Fe+Fm
- Substituting the expressions for Fe and Fm:
F=qE+q(v×B)
5. Final expression for the net force:
- Therefore, the total force on the charge q can be expressed as:
F=qE+q(v×B)
Final Answer:
The force on the charge q moving in the presence of electric field E and magnetic field B is:
F=qE+q(v×B)
- The charge q experiences two types of forces: one due to the electric field and another due to the magnetic field.
- The force Fe on the charge due to the electric field E is given by the formula:
Fe=qE
- Here, q is the charge and E is the electric field strength.
- The force Fm on the charge moving with velocity v in a magnetic field B is given by the formula:
Fm=q(v×B)
- This is a vector product, meaning the direction of the force is determined by the right-hand rule, and v is the velocity of the charge.
- The net force F acting on the charge q is the sum of the electric force and the magnetic force:
F=Fe+Fm
- Substituting the expressions for Fe and Fm:
F=qE+q(v×B)
- Therefore, the total force on the charge q can be expressed as:
F=qE+q(v×B)
The force on the charge q moving in the presence of electric field E and magnetic field B is:
F=qE+q(v×B)
Topper's Solved these Questions
Similar Questions
An electron beam with equivalent electric current I enters a region of crossed electric field and magnetic field B. Both the fields are uniform. It is found that the electron beam goes undeviated through the region of fields. After passing the field region, electrons hit a grounded target. How much force is exerted by the electron beam on urget? Assumem is the mass of electron and e its charge.
View SolutionConsider a charged particle moving with constant velocity inside a region of space where electric and magnetic field both are present. How can the fields and velocity be directed to achieve this state?
View Solution
Knowledge Check
A charge q moves in a region where electric field E and the magnetic field B both exist, then the force on its is
Aq(v×B)BqE+q(v×B)CqB+q(B×v)DqB+q(E×v)A charge particle travels along a straight line with a speed v in region where both electric field E and magnetic field b are present.It follows that
A|E|=|B| and the two field are perpendicularB|E|=v|B| and the two field are perpendicularC|B|=v|E| and the two field are parallelD|B|=v|E| and the two fields are perpendicularA charge q is moving in a magnetic field then the magnetic force does not depend upon
AChargeBMassCVelocityDMagnetic field
A fine pencil of β-particles, moving with a speed v, enters a region (region I), where a uniform electric field and a uniform magnetic field are both present. These β-particles then move into region II where only the magnetic field, (out of the two fields present in region I) exists. The path of the β-particles, in the two regions is as shown in the figure.
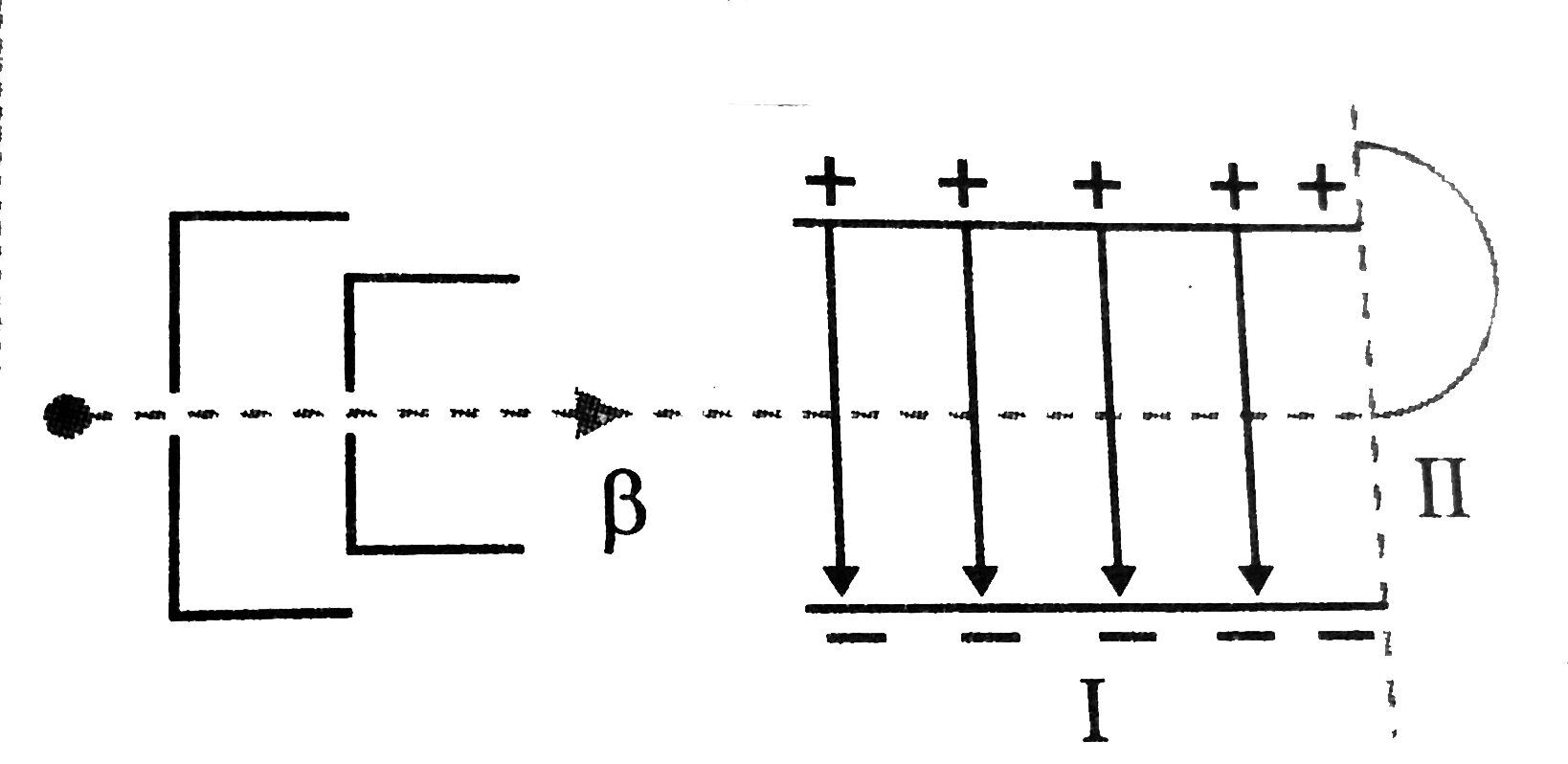
(i) state the direction of magnetic field.
(ii) state the relation between E and B in region I.
(iii) Drive the expression for the radius of the circular path of the β-particle in region II.
(iv) If the magnitude of magnetic field, in region II is changed to n times its earlier value, (without changing the magnetic field in region I) find the factor by which the radius of this circular path would change.
View SolutionWrite the expression for the force →F, acting on a charged particle of charge q moving with a velocity →v in the pressure of both electric field →E and magnetic field →B. Obtain the condition under which the particle moves undeflected through the fields.
View SolutionWrite the expression for the force →F acting on a charged particle of charge q moving with a velocity →v in the presence of both electric field →E and magnetic field →B . Obtain the condition under which the particle moves underflected through the fields.
View SolutionIn a region where both non-zero uniform electric field and magnetic field coexist, the path of a charged particle
View SolutionA charged particle moves undeflected in a region of crossed electric and magnetic fields. If the electric field is switched off, the particle has an initial acceleration a. If the magnetic field is switched off, instead of electric field, the particle will have an initial acceleration
View Solution
