Consider a charged particle moving with constant velocity inside a region of space where electric and magnetic field both are present. How can the fields and velocity be directed to achieve this state?

Text Solution

Verified by Experts

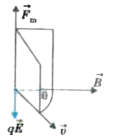
Let us assume it as one positive charge and for the negative charge, directions of fields will be + just opposite. Electric field applies force on the positive charge in its direction. And direction of magnetic force is governed by right hand rule as described in $\to F = q \to v \times \to B$ To make net force zero we require $\to v \times \to B$ opposite to $\to E$ . We know that the direction of cross product is always perpendicular to the common plane of those two vectors in cross product. So we can say that both $\to v and \to B$ must be perpendicular to $\to E$ . You can now visualise the whole situation as follows: Draw a plane perpendicular to electric field intensity vector. Velocity vector and magnetic field R V intensity vector both must lie on this plane. Angle between velocity vector and magnetic field intensity vector can be other than $90^{\circ}$ also. Let this angle be $θ$ . Now orientation of velocity vector and magnetic field intensity vector on this plane must be such that cross product is antiparallel to electric field, which is already perpendicular to this plane.
For net force to become zero, we can write as follows:
$q E = q v B sin θ \Rightarrow E = B v sin θ$
if angle $θ = 90^{\circ}, then E = B v$ .

Updated on:21/07/2023

A charged particle is moving with velocity Vin magnetic field
AIts momentum changes but total energy remains same
Bboth momentum and total energy remains same
Cboth momentum and total energy change
Dtotal energy changes but momentum remains the same
A charge particle travels along a straight line with a speed v in region where both electric field E and magnetic field b are present.It follows that
A $| E | = | B |$ and the two field are perpendicular
B $| E | = v | B |$ and the two field are perpendicular
C $| B | = v | E |$ and the two field are parallel
D $| B | = v | E |$ and the two fields are perpendicular
A charged particle moving with velocity vis subjected to electric field E and magnetic field B. The particle will go undeflected if
AE is perpendicular to B.
BE is parallel to v and perpendicular to B.
CE and B both are parallel to v.
DE, B and v are mutually perpendicular but $v = \frac{E}{B}$ .