A chain is lying on a rough table with a fraction 1/n of its length hanging down from the edge of the table. if it is just on the point of sliding down from the table, then the coefficient of friction between the table and the chain is -
1n
1(n−1)
1(n+1)
n−1(n+1)
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the chain that is lying on the rough table with a fraction 1n of its length hanging down. We will derive the coefficient of friction step by step.
1. Understanding the Setup:
- Let the total length of the chain be L.
- The length of the chain hanging down from the table is Ln.
- Therefore, the length of the chain on the table is L−Ln=L(1−1n).
2. Mass of the Chain:
- Let the mass of the entire chain be M.
- The mass of the portion hanging down (length Ln) is Mn.
- The mass of the portion on the table (length L(1−1n)) is M−Mn=M(1−1n).
3. Weight of the Hanging Portion:
- The weight of the hanging portion is given by:
Whanging=mass×g=Mn⋅g
4. Normal Force on the Chain:
- The normal force acting on the portion of the chain on the table is equal to the weight of that portion:
N=(M(1−1n))g
5. Frictional Force:
- The frictional force Ff that opposes the sliding is given by:
Ff=μ⋅N
- Substituting for N:
Ff=μ⋅(M(1−1n)g)
6. Condition for the Chain on the Verge of Sliding:
- At the verge of sliding, the frictional force equals the weight of the hanging portion:
Ff=Whanging=Mn⋅g
7. Setting the Forces Equal:
- Equating the two expressions for forces:
μ⋅(M(1−1n)g)=Mn⋅g
8. Canceling Common Terms:
- We can cancel M and g from both sides (assuming M≠0 and g≠0):
μ⋅(1−1n)=1n
9. Solving for the Coefficient of Friction μ:
- Rearranging gives:
μ=1/n1−1/n=1n−1
Final Answer:
The coefficient of friction μ between the table and the chain is:
μ=1n−1
- Let the total length of the chain be L.
- The length of the chain hanging down from the table is Ln.
- Therefore, the length of the chain on the table is L−Ln=L(1−1n).
- Let the mass of the entire chain be M.
- The mass of the portion hanging down (length Ln) is Mn.
- The mass of the portion on the table (length L(1−1n)) is M−Mn=M(1−1n).
- The weight of the hanging portion is given by:
Whanging=mass×g=Mn⋅g
- The normal force acting on the portion of the chain on the table is equal to the weight of that portion:
N=(M(1−1n))g
- The frictional force Ff that opposes the sliding is given by:
Ff=μ⋅N
- Substituting for N:
Ff=μ⋅(M(1−1n)g)
- At the verge of sliding, the frictional force equals the weight of the hanging portion:
Ff=Whanging=Mn⋅g
- Equating the two expressions for forces:
μ⋅(M(1−1n)g)=Mn⋅g
- We can cancel M and g from both sides (assuming M≠0 and g≠0):
μ⋅(1−1n)=1n
- Rearranging gives:
μ=1/n1−1/n=1n−1
The coefficient of friction μ between the table and the chain is:
μ=1n−1
Topper's Solved these Questions
Similar Questions
A uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

If the chain is limiting equlibrium, what is the coefficient of friction for the contact between table and chain?View SolutionA block on table shown in is just on the edge of slipping Find the coefficient of static friction between the blocks and table
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
A uniform chain of length l is placed on rough table with length l/n (where n>1) , hanging over the edge. If the chain just begins to slide off the table by itself from this position, the coefficient of friction between the chain and the table is
A1/nB1/(n−1)C1/(n+1)D(n−1)/(n+1) - Question 2 - Select One
A unifrom heavy chain is placed on a table with a part of it hanging over the edge. It just begins to slide when this part is one-third of its length. The coefficient of friction between the table and the chain is
A12B13C23D34 - Question 3 - Select One
A uniform rope of total length l is at rest on a table with fraction f of its length hanging (see figure). If the coefficient of friction between the table and the chain is μ then
 Af=μBf=1/(1+μ)Cf=1/(1+1/μ)Df=1/(μ+1/μ)
Af=μBf=1/(1+μ)Cf=1/(1+1/μ)Df=1/(μ+1/μ)
A uniform chain of length l is placed on a rough table, with length l/3 hanging over the edge. If the chain just begins to slide off the table by itself from this portion, the coefficient of friction between the chain and the table is 1/K. Then find the value of K.
View Solution25% of a uniform chain hangs from the edge of a horizontal table top. If the chain is on the verge of sliding,the coefficient of static friction between the chain and horizontal table is
View SolutionA chain is lying on a smooth table with half its length hanging over the edge of the table [fig(i)]. If the chain is released it slips off the table in time t1. Now, two identical small balls are attached to the two ends of the chain and the system is released [fig(ii)]. This time the chain took t2 time to slip off the table. Which time is larger, t1 or t2?
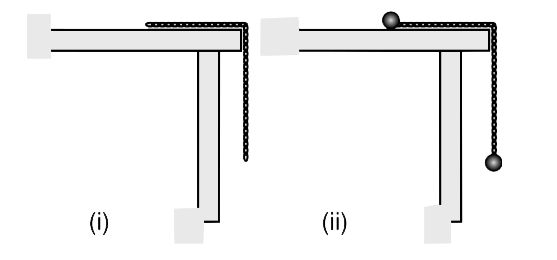 View Solution
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

If a gentale pull is given to hanging end, it will start moving down. What is the change in gravitational potential energy of the chain, as it jist leaves the table?View SolutionA small box resting on one edge of the table is struck in such a way that it slides off the other edge, 1 m away, after 2 seconds. The coefficient of kinetic friction between the box and the table -
View Solution

