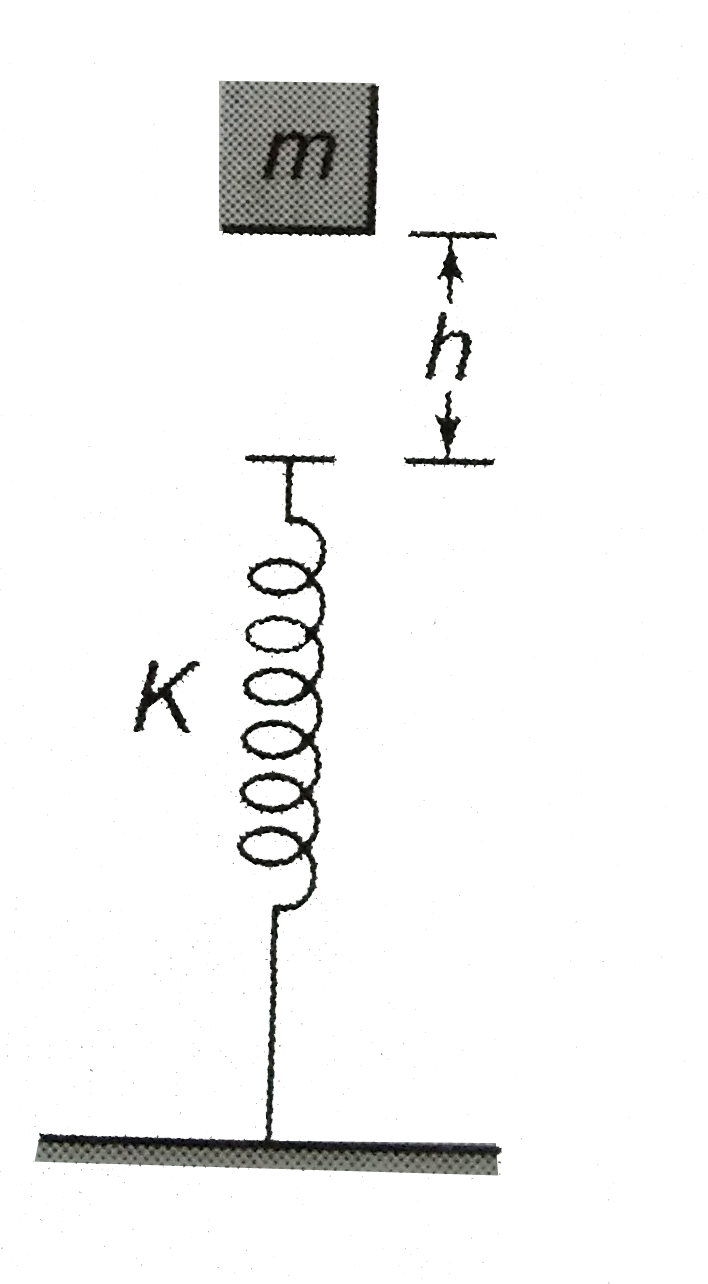Block is taken toward left so that spring is compressed. Now the block is released from rest. Block move on smooth horizontal surface after leaving spring, then on circular path R. By how much distance spring should be compressed so that block can complete circular motion :-

R√3
R√10
5R
52R
The correct Answer is:B
Mechanical Energy conservation
12kx2=12m(5rg)
mg2Rx2=5mgR

Topper's Solved these Questions
Similar Questions
Knowledge Check
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0The spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
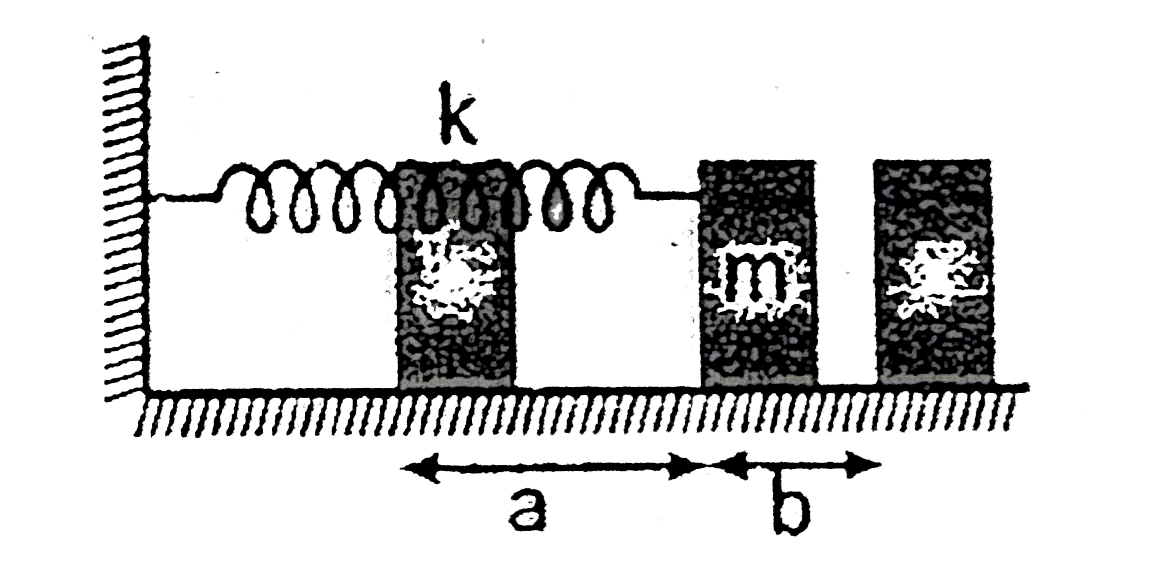 Awork done by sprinn on the block =12k(a+b)2Bwork done by sprinn on the block =12k(a2−b2)Cco-eff. of frication =k(a−b)2mgDco-eff. of frication =k(a+b)2mg
Awork done by sprinn on the block =12k(a+b)2Bwork done by sprinn on the block =12k(a2−b2)Cco-eff. of frication =k(a−b)2mgDco-eff. of frication =k(a+b)2mgA block of mass m is pushed up against a spring, compressing it a distance x, and the block is then released. The spring projects the block along a frictionaless horizontal surface, grving the block a speed v. The same spring projects a second block of mass 4m, giving it a speed 3v. What distance was the spring compressed in the second case ?
A6xBx6C36xD12x
The spring is compressed by a distance a and released. The block again comes to rest when the spring is elongated by a distance b. During this
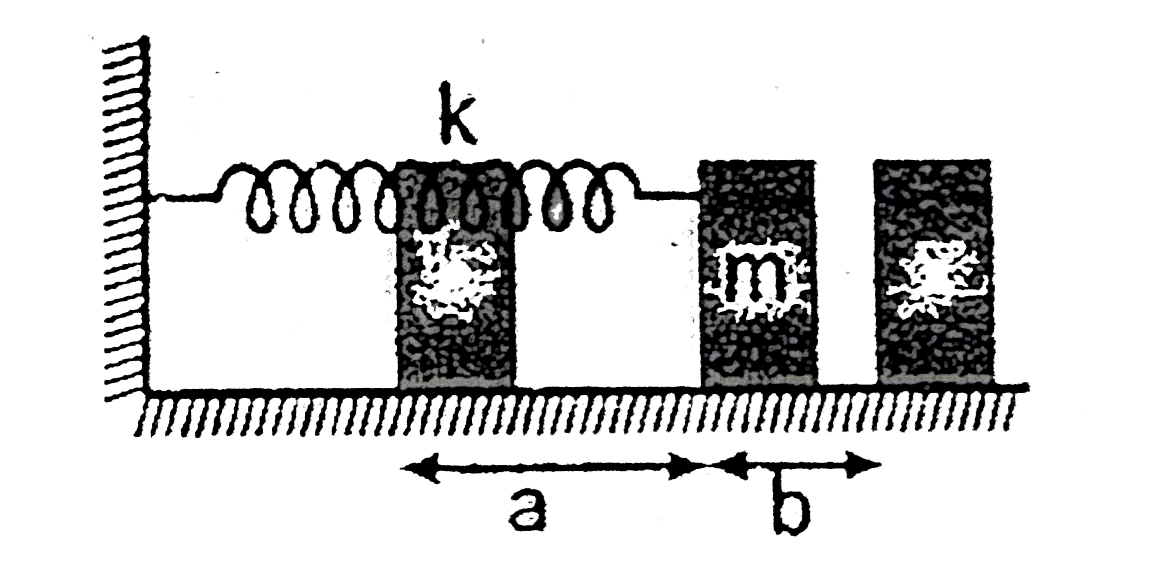
View SolutionThe block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m

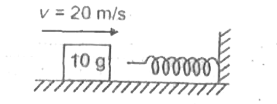
View SolutionA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
View SolutionA block of mass m rigidly attached with a spring k is compressed through a distance A. If the block is released, the period of oscillation of the block for a complete cycle is equal to

View SolutionA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is

View Solution