In Fig. 4.30, two identical parallel plate air capacitors are connected to a battery. At first the key S is closed and then it is opend. The space between the two capacitors are now filled up with a dielectric, having dielectric constant 3. Determine the ratio of the energy stored in the two capacitors before and after insertion of the dielectric?

Text Solution

Verified by Experts

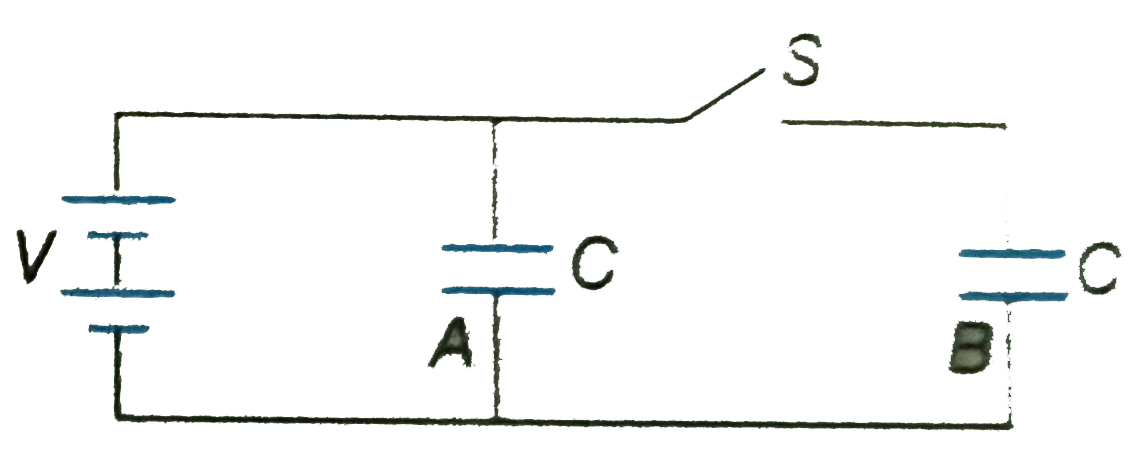
When the key was closed, potential of each capacitor was equal. Let this value of potential be V.
Energy of the capacitor $A = \frac{1}{2} C V^{2}$
and energy of the capacitor $B = \frac{1}{2} C V^{2}$
Total energy $= \frac{1}{2} C V^{2} + \frac{1}{2} C V^{2} = C V^{2}$
When the key is opened and the intervening space is filled up with the dielectric of each capacitor becomes 3C.
Since the capacitor A is still connected to the battery, its potential remains at V.
Energy of the capacitor A
$= \frac{1}{2} \times 3 C \times V^{2} = \frac{3}{2} C V^{2}$
Total charge of the capacitor B,Q = CV
This charge of B remains unaltered even after opening the key and inserting the dielectric.
Energy of $B = \frac{1}{2} \cdot \frac{Q^{2}}{3 C} = \frac{1}{2} \frac{C^{2} V^{2}}{3 C} = \frac{C V^{2}}{6}$
Energy of the two capacitors $= \frac{3}{2} C V^{2} + \frac{1}{2} C V^{2} = \frac{5}{3} C V^{2}$
The required ratio $= \frac{C V^{2}}{(\frac{5}{3}) C V^{2}} = \frac{3}{5}$ .

Updated on:21/07/2023

Two parallel plate air filled capacitors each of capacitance C, are joined in series to a battery of emf V. The space between the plates of one of the capacitors is then completely filled up with a uniform dielectric having dielectric constant K. The quantity of charge which flows through the battery is -
A $\frac{C V}{2} (\frac{K - 1}{K + 1})$
B $\frac{C V}{2} (\frac{K + 1}{K - 1})$
C $C V (\frac{K - 1}{K + 1})$
D $C V (\frac{K + 1}{K - 1})$