8 players compete in a tournament, everyone plays everyone else just once. The winner of a game gets 1, the loser 0 or each gets 1/2 if the game is drawn. The final result is that every one gets a different score and the player placed at second gets the same score as the total of four bottom players.
Step by step video & image solution for 8 players compete in a tournament, everyone plays everyone else just once. The winner of a game gets 1, the loser 0 or each gets 1/2 if the game is drawn. The final result is that every one gets a different score and the player placed at second gets the same score as the total of four bottom players. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Three players play a total of 9 games. In each game, one person wins and the other two lose; the winner gets 2 points and the losers get -1 each. The number of ways in which they can play all the 9 games and finish each with a zero score is
View SolutionSixteen players S1,S2,…,S16 play in a tournament. They are divided into eight pairs at random. From each pair a winner is decided on the basis of a game played between the two players decided to the basis of a game played between the two players of the pair. Assume that all the players are of equal strength.
(a) Find the prabability that the player S1 is among the eight winners.
(b) Find the probability that exactly one of the two players S1andS2 is among the eight winners.
View Solution
Knowledge Check
A, B, C D, ..................X, Y, Z are the players who participated in a tournament. Everyone played with every other player exactly once. A win scores 2 points, a draw scores 1 point and a loss scores 0 points. None of the matches ended in a draw. No two players scored the same score. At the end of the tournament, the ranking list is published which is in accordance with the alphabetical order. Then
AM wins over NBN wins over MCM does not play with NDNone of theseIn each of a set of games it is 2 to 1 in favour of the winner of the previous game. The chance that the player who wins the first game shall win three at least of the next four is
A827B481C49DNone of theseFive friends decided to play a game of badminton. Each of the five playsagainst everyother friends. The winner gets two points for each game he or she wins and the loser gets zero . Then which of the following cannot represent the scores of five friends ?
A4, 4, 4, 4, 4B6, 4, 4, 4, 2C8, 8, 2, 2, 0D6, 6, 4, 2, 2
In each of a set of games it is 2 to 1 in favor of the winner of the previous game: what is the chance that the player who wins the first game shall win three at least of the next four.
View SolutionAnswer the questions on the basis of the information given below: Coach John sat with the score cards of Indian players from the 3 games in a one-day cricket tournament where the same set of players played for India and all the major batsman got out. John summarized the batting performance through three diagrams, one for each game. In each diagram, the three outer triangles communicate the number of runs scored by the three top scorers from India, where K, R, S,V and Y represent Kaif, Rahul, Saurav, Virender, and Yuvraj respectively. The middle triangle in each diagram denotes the percentage of total score that was scored by the top three Indian scorers in that game. No two players score the same number of runs in the same game. John also calculated two batting indices for each player based on his scores in the tournament, the R-index of a batsman is the difference between his highest and lowest scores in the 3 games while the M-index is the middle number, if his scores are arranged in a non-increasing order.
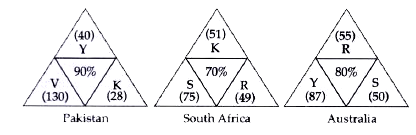
Which of the players had the best M-index from the tournament?
View SolutionAnswer the questions on the basis of the information given below: Coach John sat with the score cards of Indian players from the 3 games in a one-day cricket tournament where the same set of players played for India and all the major batsman got out. John summarized the batting performance through three diagrams, one for each game. In each diagram, the three outer triangles communicate the number of runs scored by the three top scorers from India, where K, R, S,V and Y represent Kaif, Rahul, Saurav, Virender, and Yuvraj respectively. The middle triangle in each diagram denotes the percentage of total score that was scored by the top three Indian scorers in that game. No two players score the same number of runs in the same game. John also calculated two batting indices for each player based on his scores in the tournament, the R-index of a batsman is the difference between his highest and lowest scores in the 3 games while the M-index is the middle number, if his scores are arranged in a non-increasing order.

Among the players mentioned, who can have the lowest R-index from the tournament ?
View SolutionStudy the given information carefully and answer the following questions.
There was a football tournament of three teams i.e. A, B and C in which each team played 2 matches. Score pattern of the tournament is:
• A team gets 2 points for scoring a goal against the opponent team.
• A team gets 3 points for scoring a goal against the opponent team from the outside area.
• There is a penalty of 1 point if a team concedes a goal.
• Only three players from each team scored the goals.
A – B Match: B is the winner of this game. Total points scored by B in this match is 4 . Also, team A scored 2 goals and none of the players scored the goal from the outside area.
A – C Match: C scored 0 points in the match. Only one player from team A scored a goal from outside area. A scored 4 points in this match.
B – C Match: B gets 6 points from match. Team C scored 1 goal more than Team B. One player from team B scored a goal from outside area but none from team C.
The given 3 teams are ranked on the basis of total marks in such a way that the highest scoring team is ranked 1, the second highest scoring team is ranked 2 and the least scoring team is ranked 3. Rank 3 got a total of Rs. 60,000 as prize money. If the ratio of the prize money of the rank 1, rank 2 and rank 3 team is 8 : 5 : 3, which of the following combinations of team and prize money is correct?
View SolutionStudy the given information carefully and answer the following questions.
There was a football tournament of three teams i.e. A, B and C in which each team played 2 matches. Score pattern of the tournament is:
• A team gets 2 points for scoring a goal against the opponent team.
• A team gets 3 points for scoring a goal against the opponent team from the outside area.
• There is a penalty of 1 point if a team concedes a goal.
• Only three players from each team scored the goals.
A – B Match: B is the winner of this game. Total points scored by B in this match is 4 . Also, team A scored 2 goals and none of the players scored the goal from the outside area.
A – C Match: C scored 0 points in the match. Only one player from team A scored a goal from outside area. A scored 4 points in this match.
B – C Match: B gets 6 points from match. Team C scored 1 goal more than Team B. One player from team B scored a goal from outside area but none from team C.
What is the maximum possible sum of the total number of goals scored by those players of all three teams, who score more than one goal in a tournament?
View Solution
