The graph betwee and is (E=kinetic energy and p= momentum)
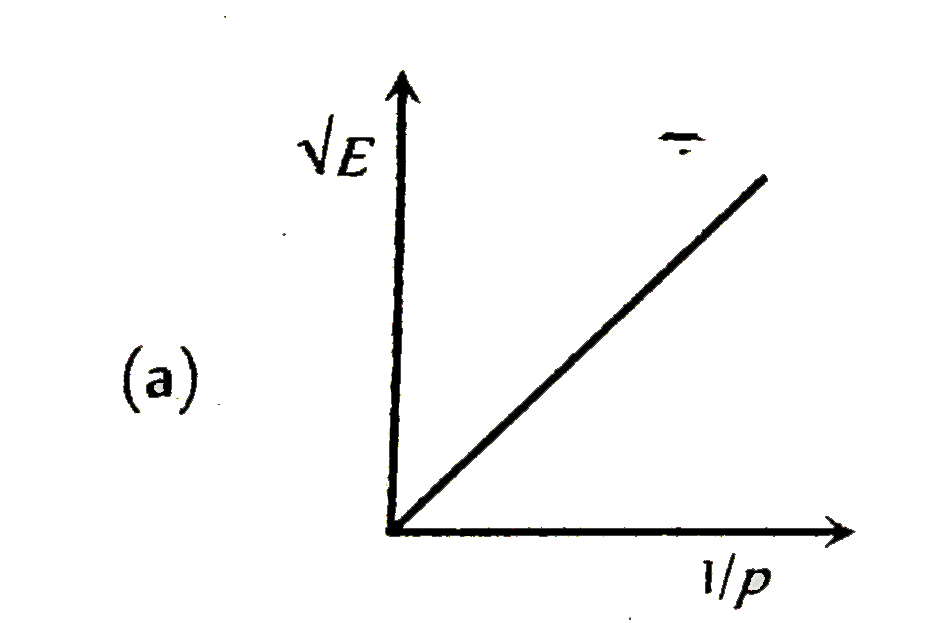
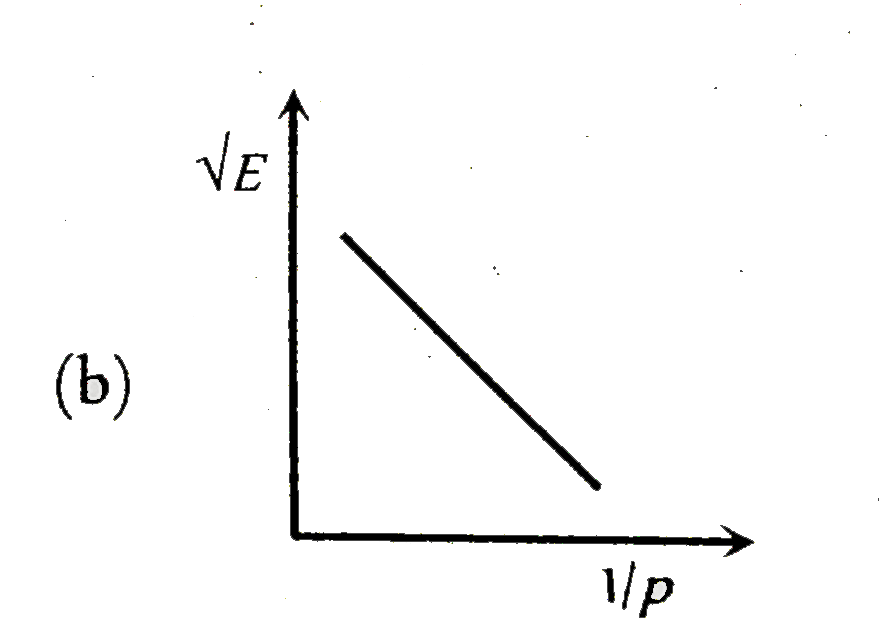

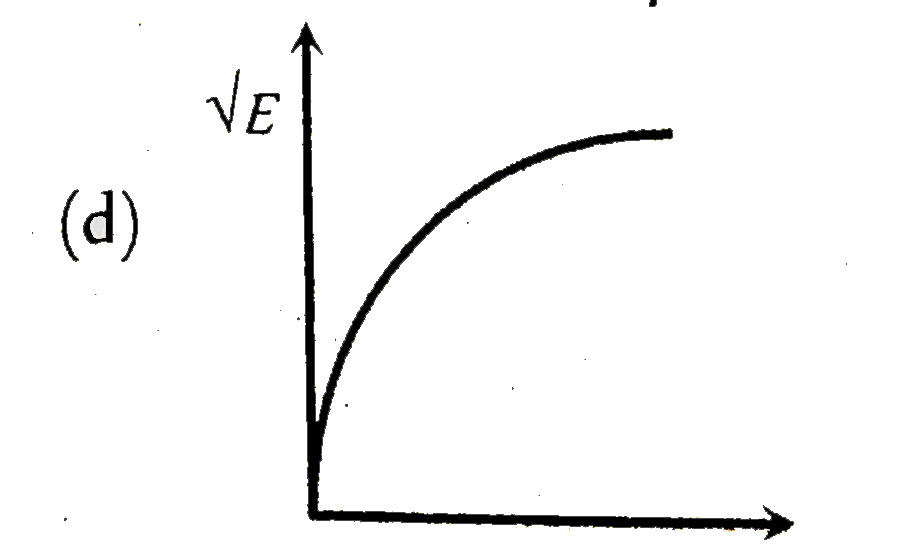
The correct Answer is:C
To analyze the relationship between the square root of kinetic energy (E) and the reciprocal of momentum (p), we can follow these steps:
1. Understanding Kinetic Energy and Momentum:
- The kinetic energy (E) of an object is given by the formula:
E=12mv2
- The momentum (p) of an object is defined as:
p=mv
2. Expressing Kinetic Energy in terms of Momentum:
- From the momentum equation, we can express velocity (v) as:
v=pm
- Substituting this expression for v into the kinetic energy formula:
E=12m(pm)2
- Simplifying this gives:
E=12m⋅p2m2=p22m
3. Rearranging the Equation:
- We can rearrange the equation to express E in terms of p:
E=12mp2
- This shows that E is proportional to the square of momentum.
4. Finding the Relationship Between √E and 1p:
- Taking the square root of both sides:
√E=√12m⋅p
- Rearranging gives:
\sqrt{E} = K \cdot p \quad \text{(where K = \sqrt{\frac{1}{2m}} )}
- Now, substituting p=11p:
√E=K⋅11p
5. Final Form of the Equation:
- If we let Y=√E and X=1p, we can write:
Y=K⋅1X
- This is the equation of a rectangular hyperbola.
6. Conclusion:
- The graph of √E versus 1p will be a rectangular hyperbola.
- The kinetic energy (E) of an object is given by the formula:
E=12mv2
- The momentum (p) of an object is defined as:
p=mv
- From the momentum equation, we can express velocity (v) as:
v=pm
- Substituting this expression for v into the kinetic energy formula:
E=12m(pm)2
- Simplifying this gives:
E=12m⋅p2m2=p22m
- We can rearrange the equation to express E in terms of p:
E=12mp2
- This shows that E is proportional to the square of momentum.
- Taking the square root of both sides:
√E=√12m⋅p
- Rearranging gives:
\sqrt{E} = K \cdot p \quad \text{(where K = \sqrt{\frac{1}{2m}} )}
- Now, substituting p=11p:
√E=K⋅11p
- If we let Y=√E and X=1p, we can write:
Y=K⋅1X
- This is the equation of a rectangular hyperbola.
- The graph of √E versus 1p will be a rectangular hyperbola.
Topper's Solved these Questions
Similar Questions
(a) A proton is moving at a speed much less than the speed of light. It has kinetic energy K1 and momentum p1. If the momentum of the proton is doubled, so p2=2p1, how is its new kinetic energy K2 related to K−1?
(b)A photon with energy E1 has momentum p1 . if another photon has momentum p2 that is twice p1, how is the energy E2 of the second photon related to E1?
View SolutionRelation between kinetic energy and momentum
Let us consider a body of mass 'm' having a velocity 'v', then
momentum of the body P = mass × velocity
P=m×v⇒v=Pm ...(1)
From definition, kinetic energy (K.E) of the body
K.E=12mv2 ...(2)
Now putting the value of (1) in (2) we have
K.E=12m(Pm)2
K.E.=12mP2m2=12P2m=P22m ...(3)
Thus we can write
P2=2m×K.E
⇒P=√2m×K.E
Thus momentum = √2×mass×kinetic energy
What will be the momentum of a body of mass 100 g having kinetic energy of 20 J ?
View Solution
Knowledge Check
The graph between linear monentum (p) and Kinetic energy (k) is best represented by
A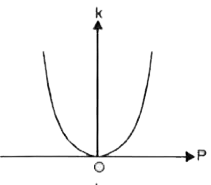 B
B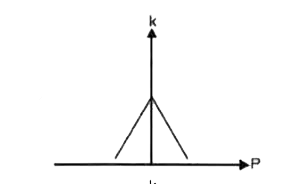 C
C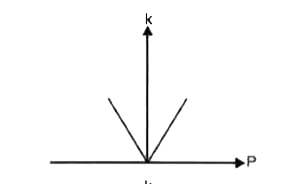 D
D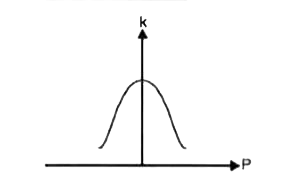
The relation between kinetic energy K and linear momentum p of a particle is represented by
AK2=2mpB2K2=mpCp2=2mkD2mK=pThe relation between kinetic energy K and linear momentum p of a particle is represented by
AK2=2mpB2K2=mpCp2=2mKD2mK=p
The momentum of a body is p and its kinetic energy is E. Its momentum becomes 2p. Its kinetic energy will be
View SolutionAn electron with speed v and a photon with speed c have the same de-Broglic wavelength. If the kinetic energy and momentum of electron is Ee and Pe and that of photon is Eph and Pph respectively, then correct statement is -
View SolutionThe curve between loge L and loge P is (L is the angular momentum and P is the linear momentum).
View SolutionWhich of the following graphs represents the graphical relation between momentum (p) and kinetic energy (K) for a body in motion?
View SolutionWhich one of the following correctly represents the variation between linear momentum (P) and kinetic energy (E) ofa body?
View Solution