For an orbital , having no planar angular nodes following the equation :
Ψ(r)=Ke−r/K'.r2(K''−r)
Identify the orbital :
4dz2
2s
3dz2
4dxy
The correct Answer is:A
Step by step video, text & image solution for For an orbital , having no planar angular nodes following the equation : Psi_((r)) = Ke^(-r//K') dot" r^(2)(K'' -r) Identify the orbital : by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - ATOMIC STRUCTUREEXERCISE - Reasoning Type11videos
ATOMIC STRUCTURE
- BOOK - GRB PUBLICATIONCHAPTER - ATOMIC STRUCTUREEXERCISE - Multiple Objective Type49videos
ATOMIC STRUCTURE
- BOOK - GRB PUBLICATIONCHAPTER - ATOMIC STRUCTUREEXERCISE - de Brogile and Heisenberg43videos
ATOMIC STRUCTURE
- BOOK - GRB PUBLICATIONCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - D.Le Chateliera principle16videos
CHEMICAL EQUILIBRIUM
Similar Questions
Knowledge Check
- Question 1 - Select One
A test particle is moving in a circular orbit in the gravitational field produced by a mass density ρ(r)=Kr2. Identify the correct relation between the radius R of the particle’s orbit and its period T:
AT/R is constantBTR is a constantCT2/R3is a constantDT/R2 is a constant - Question 2 - Select One
Two particles of identical mass are moving in circular orbits under a potential given by V(r)=Kr−n, where K is a constant. If the radii of their orbits are r1,r2 and their speeds are v1,v2, respectively, then
Av21rn1=v22rn2Bv21r−n1=v22r−22Cv21r1=v22r2Dv21r2−n1=v22r2−n2 - Question 3 - Select One
Ψ(r)=ke−r/k1.r2(r2−k2r+k3) . If the orbital has no nodal plane , then , orbital can be :
A5dxyB5dC4dz2D4px
Mr. Santa has to decode a number “ABCDEF” where each alphabet is represented by a single digit. Suppose an orbital whose radial wave functional is represented as :
ψ(r)=k1e−r/k2(r2−5k3r+6k23)
From the following information given about each alphabet then write down the answers in the form of “ABCDEF”, for above orbital.
Info A = Value of n where “n” is principal quantum number.
Info B = No. of angular nodes
Info C = Azimuthal quantum number of subshell to orbital belongs
Info D = No. of subshells having energy between (n+5) s to (n+5) p where n is principal quantum number.
Info E = Orbital angular momentum of given orbital.
Info F = Radial distance of the spherical node which is farthest from the nucleus.
(Assuming k3=1))View SolutionMr.Santa has to decode a number "ABCDEF" where each alphabet is respersented by a single digit .
Suppose an orbital whose radial wave functoin id respresented as
Ψr=K1.e_r/k2(r2−5k3r+k23)
From the following information given about each alphabet then write down the answer in the from of
"ABCDEF" , for above orbital .
Info A= Value of n where "n" is principle quantum number
Info B= No .of angular nodes
InfoC=Azimuthal quantum number of subshell to orbital belongs
Info D= No. of subshells having energy between (n+5)s to (n+5)p where n id principle quantum
number
Info E=Orbital angular momentum of given orbital.
Info F= Radial distance of the spherical node which is farthest from the nuclues
(Assuming K3 =1)View SolutionA satellite of mass m orbits the earth in an elliptical orbit having aphelion distance ra and perihelion distance rp. The period of the orbit is T. The semi-major and semi-minor axes of the ellipse are ra+rp2 and √ρpra respectively. The angular momentum of the satellite is :
View SolutionFor an orbital the graph between ψ(r) and r (distance from nucles) is :
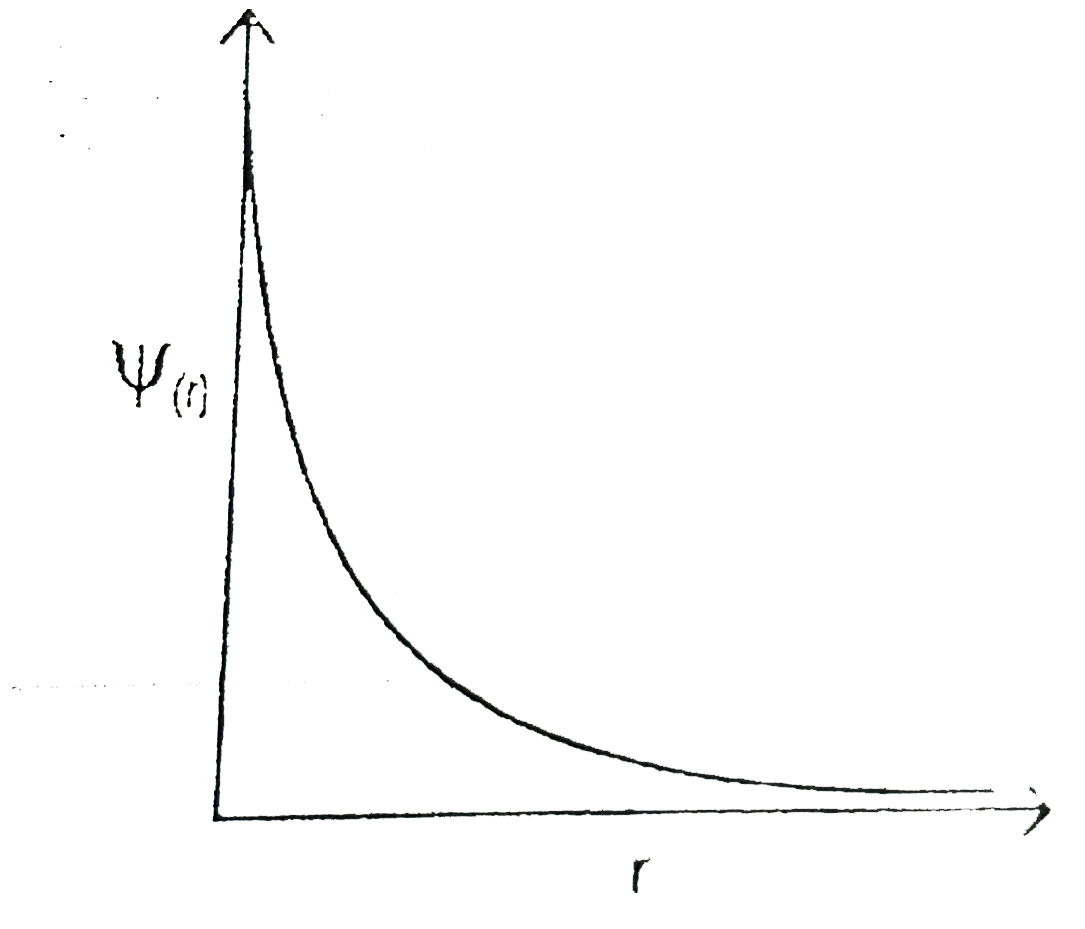
Find the value of n+l of the orbital.View SolutionA test particle is moving in a circular orbit in the gravitational field produced by a mass density ρ(r)=Kr2. Identify the correct relation between the radius R of the particle’s orbit and its period T:
View Solution

