If u1 and u2 are the units selected in two systems of measurement and n1 and n2 their numerical values, then
n1u1=n2u2
n1u1+n2u2=0
n1n2=u1u2
(n1+u1)=(n2+u2)
The correct Answer is:A
Step by step video, text & image solution for If u_(1) and u_(2) are the units selected in two systems of measurement and n_(1) and n_(2) their numerical values, then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
If u1,u2 and v1,v2 are the initial and final velocities of two particles before and after collision respectively, then v2−v1u1−u2 is called ___________.
View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
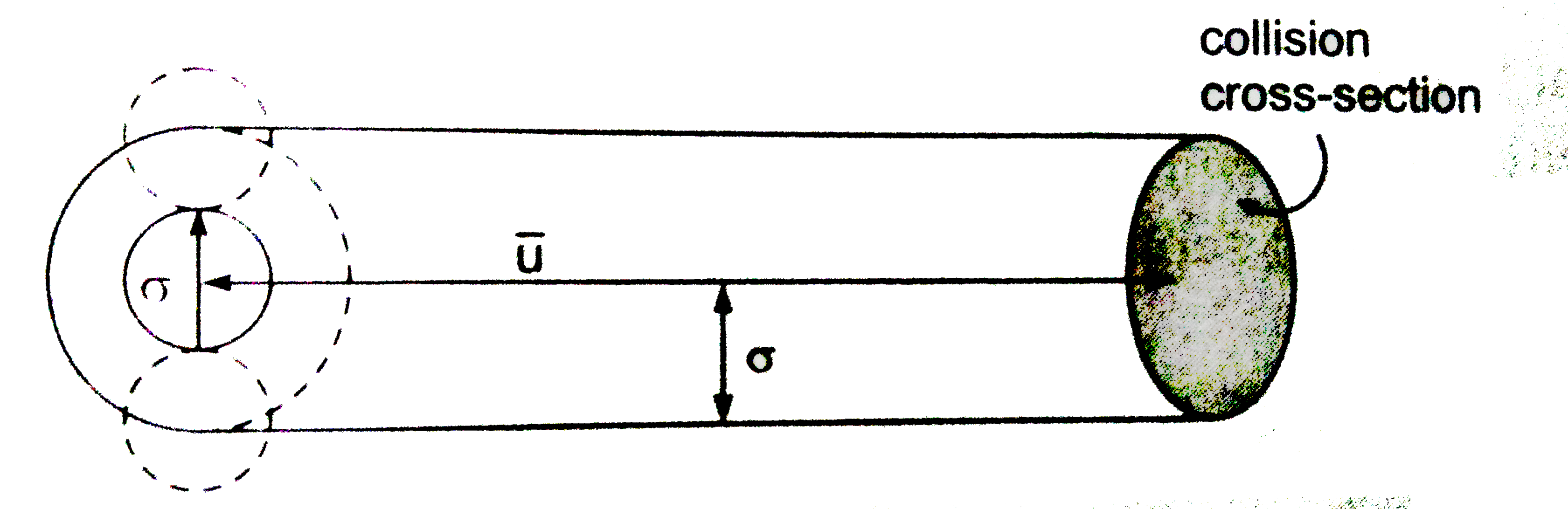
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.
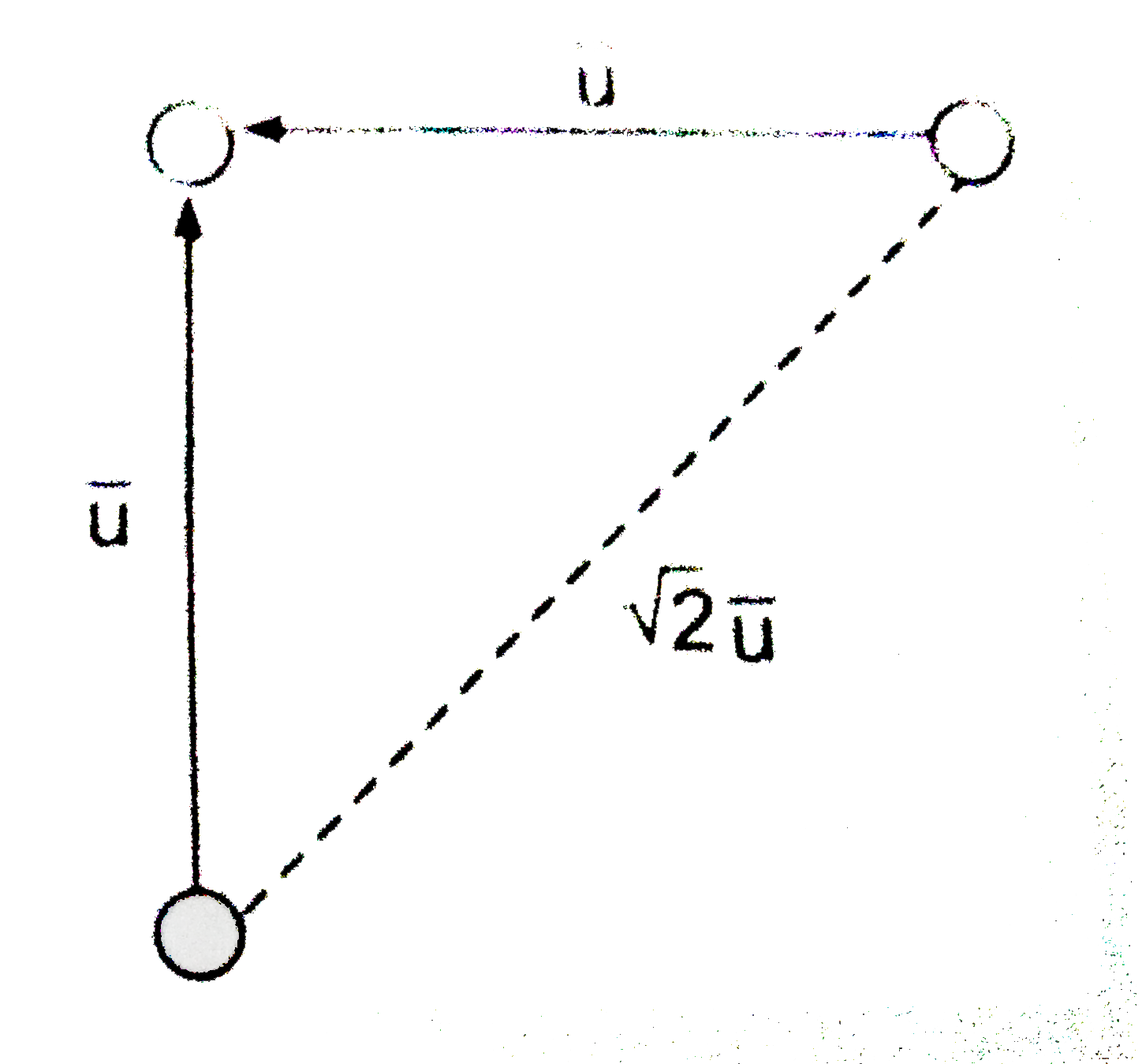
Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯2N∗
The→talνmberofbimo≤ca––rcollisionsZ_(1)perunitvolumeperunittimeisgivenby<br>Z_(1)=(1)/(2)(Z_(1)N^(**))or Z_(11)=(1)/(2)(sqrt(2)pisigma^(2)overline(u)N^(**))N^(**)=(1)/(sqrt(2))pisigma^(2)overline(u)N^(**2)<br>Ifthecollsion∈volvetwounlikemo≤ce–sthentheνmberofcollisionsZ_(12)perunitvolumeperunittimeisgivenas<br>Z_(12)= pisigma _(12)^(2)(sqrt((8kT)/(pimu)))N_(1)N_(2)<br>whereN_(1)andN_(2)aretheνmberofmo≤ce–sperunitvolumeofthetwotypesofmo≤ce–s,sigma_(12)istheavera≥diameterofthetwomo≤ce–sandmuisthereducedmass.Themeaneepathistheavera≥distancetravel≤dbyamo≤ce–betweentwo≻essivecollisions.Wecanexpressitasfollows:<br>lambda=("Average distance travelled per unit time")/("NO. of collisions made by a single molecule per unit time")=(overline(u))/(Z_(1))<br>or" "lambda=(overline(u))/(sqrt(2)pisigma^(2)overline(u)N^(**))implies(1)/(sqrt(2)pisigma^(2)overline(u)N^(**))<br>Threealgassamp≤s∈separateequalvolumeconta∈ersaretakenandfollow∈gdataisgiven:<br> PressureTemperatureMean free pathsMol.wt.Gas A1atm1600K0.16nm20Gas B2atm200K0.16nm40Gas C4atm400K0.04nm80
Calculate number of collision by one molecule per sec (Z1).View Solution
Knowledge Check
- Question 1 - Select One
If u1andu2 are the selected in two system of measurement and n1andn2 their nomerical values, then
An1u1=n2u2Bn1u1+n2u2=0Cn1n2=u1u2D(n1+u1)=(n2+u2) - Question 2 - Select One
Collision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
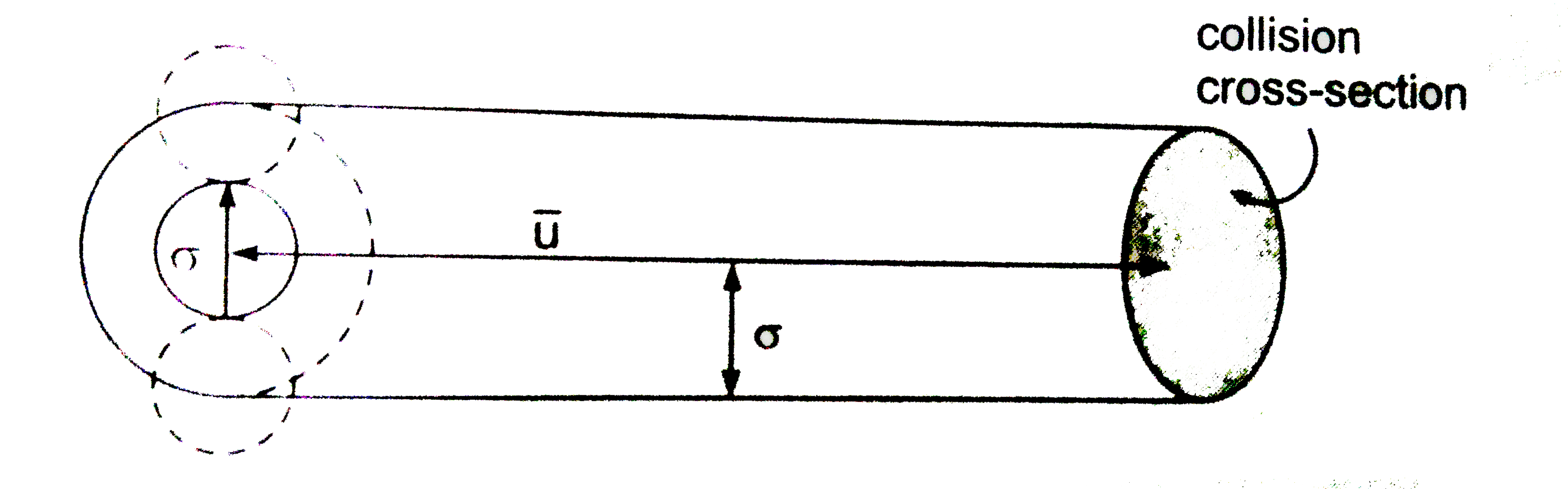
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
Three ideal gas samples in separate equal volume containers are taken and following data is given :
PressureTemperatureMean free pathsMol.wt.Gas A1atm1600K0.16nm20Gas B2atm200K0.16nm40Gas C4atm400K0.04nm80
Calculate ratio of collision frequencies (Z11)(A:B:C) of following for the three gases.A1:2:4B4:2:1C1:4:16D16:4:1 - Question 3 - Select One
Collision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is

V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
Three ideal gas samples in separate equal volume containers are taken and following data is given :
PressureTemperatureMean free pathsMol.wt.Gas A1atm1600K0.16nm20Gas B2atm200K0.16nm40Gas C4atm400K0.04nm80
Calculate number of collision by one molecule per sec (Z1).A4:1:4B1:4:4C4:3:2D1:2:4
When some object is kept at a distances u1andu2 from the concave mirror then size of images are found to be same. If magnitude of focal length can be written as (u1+u2)/n, then what will be the value of n ?
|0123456789|View SolutionCollision cross-section is an area of an imaginary sphere of radius σ around the molecule within which the centre of another molecule cannot penetrate.
The volume swept by a single molecule in unit time is
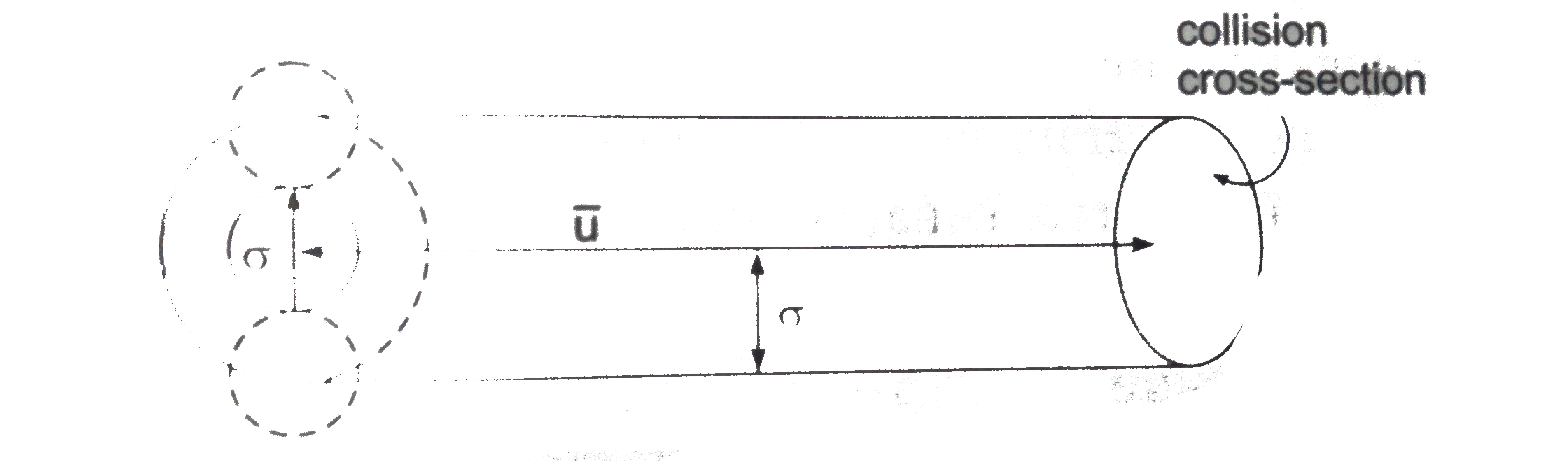
V=(πσ2)¯u where ¯u is the average speed
If N∗ is the number of molecules per unit volume, then the number of molecules within the volume V is
N=VN∗=(πσ2¯u)N∗
Hence, the number of collision made by a single molecule in unit time will be
Z=N=(πσ2¯u)N∗
In order to account for the movements of all molecules, we must consider the average velocity along the line of centres of two coliding molecules instead of the average velocity of a single molecule . If it is assumed that, on an average, molecules collide while approaching each other perpendicularly, then the average velocity along their centres is √2¯u as shown below.

Number of collision made by a single molecule with other molecule per unit time is given by
Z1=πσ2(¯urel)N∗=√2πσ2¯uN∗
The total number of bimolecular collisions Z11 per unit volume per unit time is given by
Z11=12(Z1N∗)orZ11=12(√2πσ2¯uN∗)N∗=1√2πσ2¯uN∗2
If the collsion involve two unlike molecules then the number of collisions Z12 per unit volume per unit time is given as
Z12=πσ212(√8kTπμ)N1N2
where N1 and N2 are the number of molecules per unit volume of the two types of molecules, σ12 is the average diameter of the two molecules and μ is the reduced mass. The mean free path is the average distance travelled by a molecule between two successive collisions. We can express it as follows :
λ=Average distance travelled per unit timeNO. of collisions made by a single molecule per unit time=¯uZ1
or λ=¯u√2πσ2¯uN∗⇒1√2πσ2¯uN∗
For a given gas the mean free path at a particular pressure is :View SolutionThe numerical values and units of a physical quantity in two different system of units are n1,n2andu1,u2 respectively. Then
View SolutionThe first factor length f1 for refraction at a spherical surface is defined as the value of u corresponding to v=∞ (as shown) with refractive indices of two mediums, as n1 and n2. The second focal length f2 is defined as value of v for u=∞.
 View Solution
View SolutionP(Ui)=1n, and one urn is selected at random, then P(W) is:
View Solution

