A wave pulse is generated at the bottom of a uniform string (of mass m and length l) Suspended from ceiling and supporting a block (of mass m) as shown.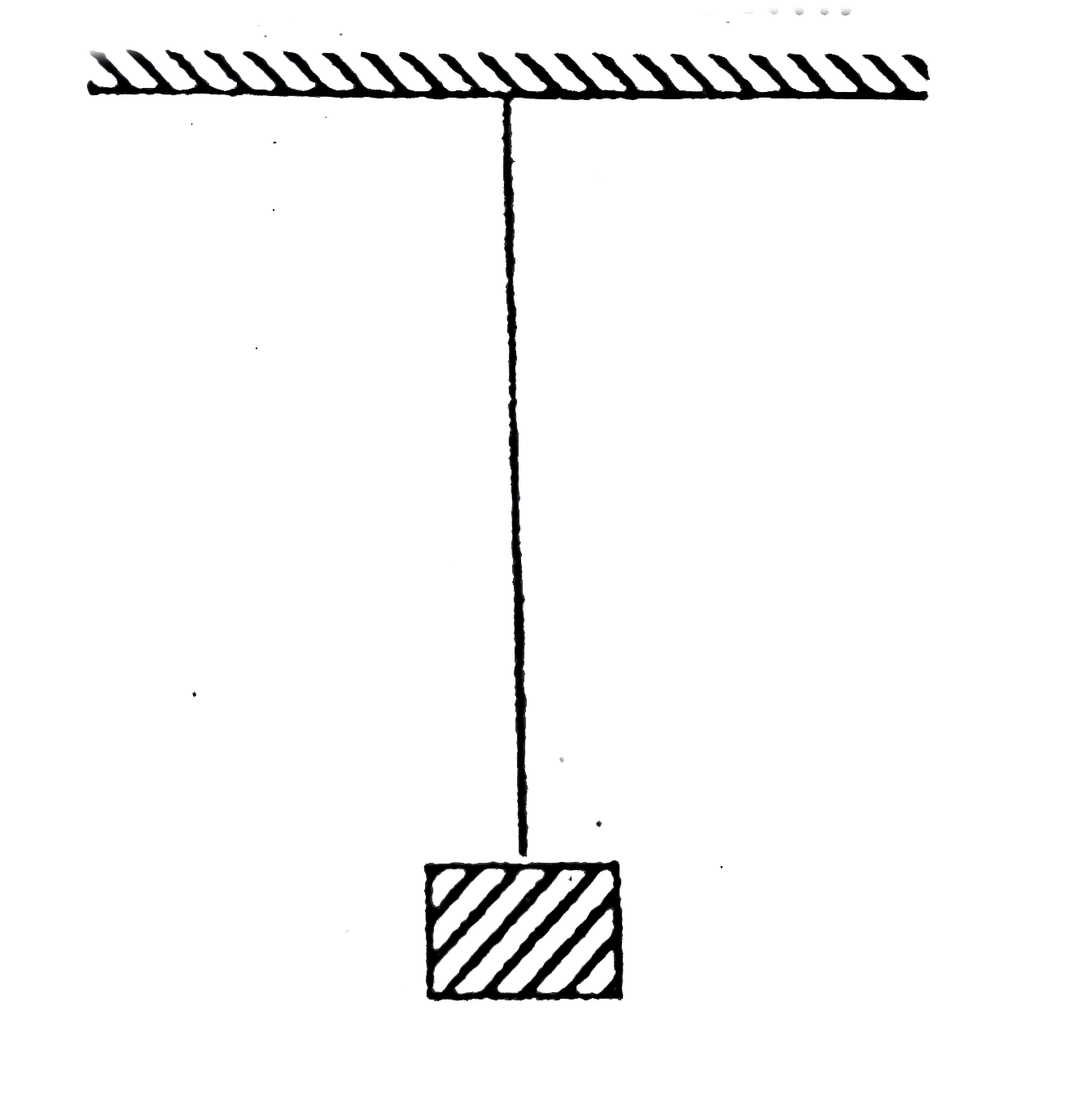 
Acceleration of the wave pulse is g2
Time taken by the wave pulse to travel from botom to ceiling is ((√2+1).2)√lg
Speed of the wave at bottom of string is √gl
Speed of the wave as it is just about to strike the ceiling is√2gl
The correct Answer is:A, C, D
At a distance x from the bottom,
V=√Tμ=√mg+mgxlml=√g(l+x)
⇒a=V.dVdx=g2
Time of motion =g2lVaverage=2l√gl+√2gl
=2(√2+1)√lg
Similar Questions
Find the time period of small oscillations of the following systems.
(a) A uniform rod of mass m and length L is suspended through a pin hole at distance L/4 from top as shown.
(b) A ring of mass m and radius r suspended through a point on its periphery.
(c) A uniform disc of mass m and radius r suspended through a point r/2 away from centre.
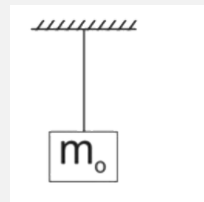
(d) A uniform square plate of edge a suspended through a corner.View SolutionThe block of mass m0=μL is attached to a uniform string of mass M=μL and length L as shown in the figure. If a wave pulse is produced near the block, then the time it taken to reach the ceiling is
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle of mass m is attached to an end of a uniform rod of mass M = 2m and length l1 which is suspended through its mid point by an inextensible string as shown initially the rod is in horizontal position and at rest. The system is released from this position Just after the release
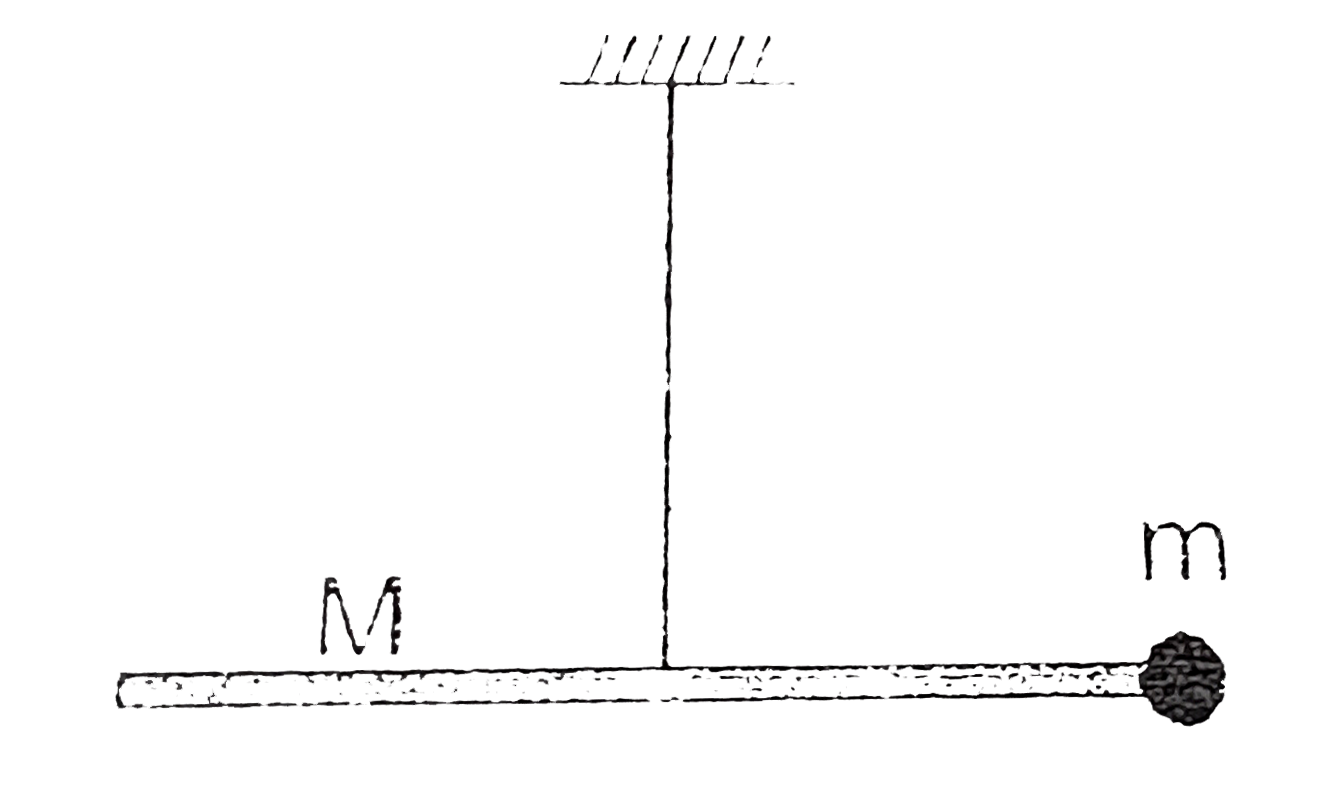AThe angular acceleration of the system is 6g5lBThe angular acceleration of the system is 2g5lCThe Tension in the string is 125mgDThe Tension in the string is 25 mg - Question 2 - Select One
An elevator accelrates upward at a constant rate. A uniform string of length L and mass m supports a small block of mass M that hangs from the celling of the elevator. The tension at distance l from the celling is T. the accelration of the elegvator is
ATM+m−ml/L−gBT2M+m−ml/L+gCTM+ml/L−gDT2M−m+ml/L−g - Question 3 - Select One or More
A block M hangs vertically at the bottom end of a uniform rope of constant mass per unit length. The top end of the rope is attached to a fixed rigid support at O. A transverse wave pulse (Pulse 1) of wavelength λ0 is produced at point O on the rope. The pulse takes time TOA to reach point A. If the wave pulse of wavelength λ0 is produced at point A (Pulse 2) without disturbing the position of M it takes time TAO to reach point O. Which of the following options is/are correct?
AThe velocities of the two pulses (Pulse 1 and Pulse 2) are the same at the midpoint of ropeBThe velocity of any pulse along the rope is independent of its frequency and wavelengthCThe wavelength of Pulse 1 becomes longer when it reaches point ADThe time TAO=TOA
One end of a uniform rod of mass M and cross-sectional area A is suspended from a rigid support and an equal mass M is suspended from the other end, what is the stress at the mid point of the rod.
View SolutionA heavy block of mass M hangs in equilibrium at the end of a rope of mass m and length l connected to a celling. Determine the tension in the rope at a distance x from the ceiling.
View SolutionA uniform rod of mass m and length L is suspended through two vertical strings of equal lengths fixed at ends. A small object of mass 2m is placed at distance L/4 from the left end. Find the tensions in the two strings.
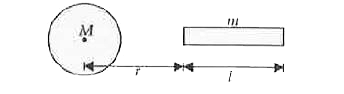
View SolutionThe gravitational force of attraction between a uniform sphere of mass M and a uniform rod of length l and mass in as shown in figure is
View SolutionA uniform cubical block of mass M is attached to a pulley. One end of a string, passing over the pulley is fixed to a light pole while is fixed on the bigger block and its another end is attached to a block of mass m as shown in figure. The maximum value of the mass m so that the block does not topple is : (string and pulley are ideal)
View Solution