A mass m is suspended from the ceiling by a string with variable linear mass density .A wave pulse is produced at the top of an oscillator which travels from top to bottom with constant wave speed. (x axis is positive downwards). Then.
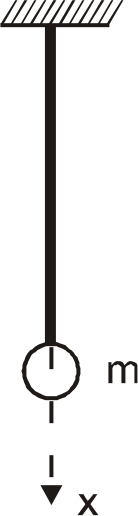
=constant
When we move along +x direction (top to bottom) x increases but T decreases
when T decreases must decrease
increases" " decreases" "
Topper's Solved these Questions
Similar Questions
A radioactive element decays by β−emission. A detector records n beta particles in 2s and in next 2s it records 0.75n beta particles. Find mean life correct to nearest whole number. Given ln |2|=0.6931, ln |3|=1.0986.
02:37View SolutionWhen p−n junction diode is forward biased then
01:12View SolutionFigure showa a string of linear mass density 1.0gcm−1onwhichawaveps–eistravell∈g.F∈dthetimetakenbytheps–e∈travell∈gthroughadistanceof50cmonthestr∈g.Takeg=10 ms^-2.
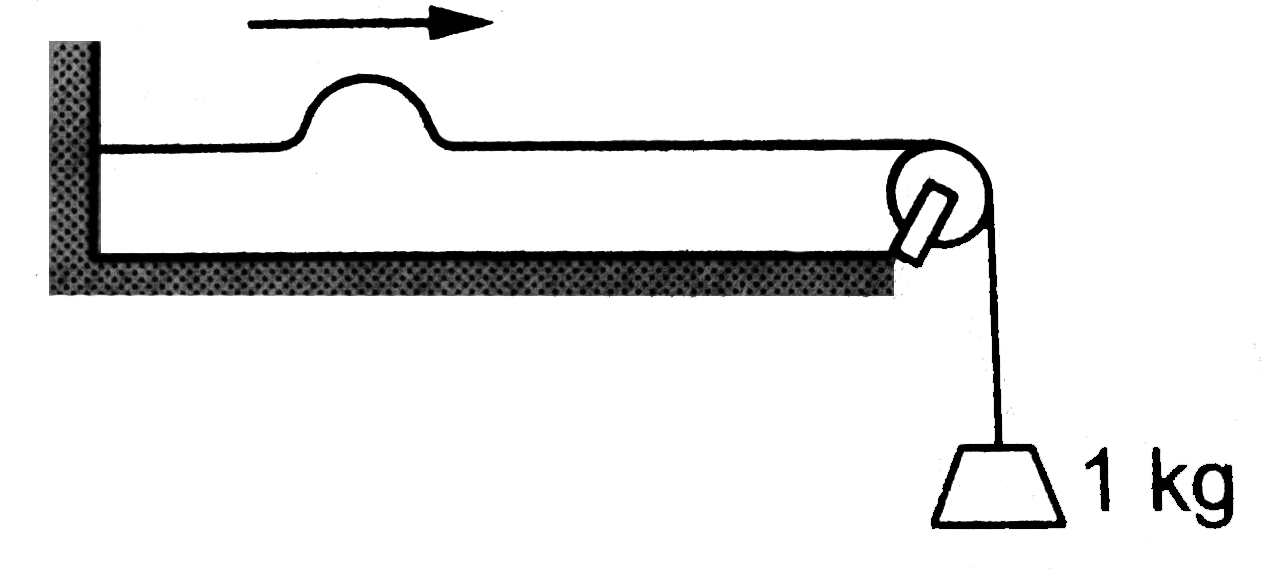 03:15View Solution
03:15View SolutionFigure shows a string of linear mass density 1.0gcm−1 on which a wave pulse is travelling. Find the time taken by pulse in travelling through a distance of 50cm on the string. Take g=10ms−2
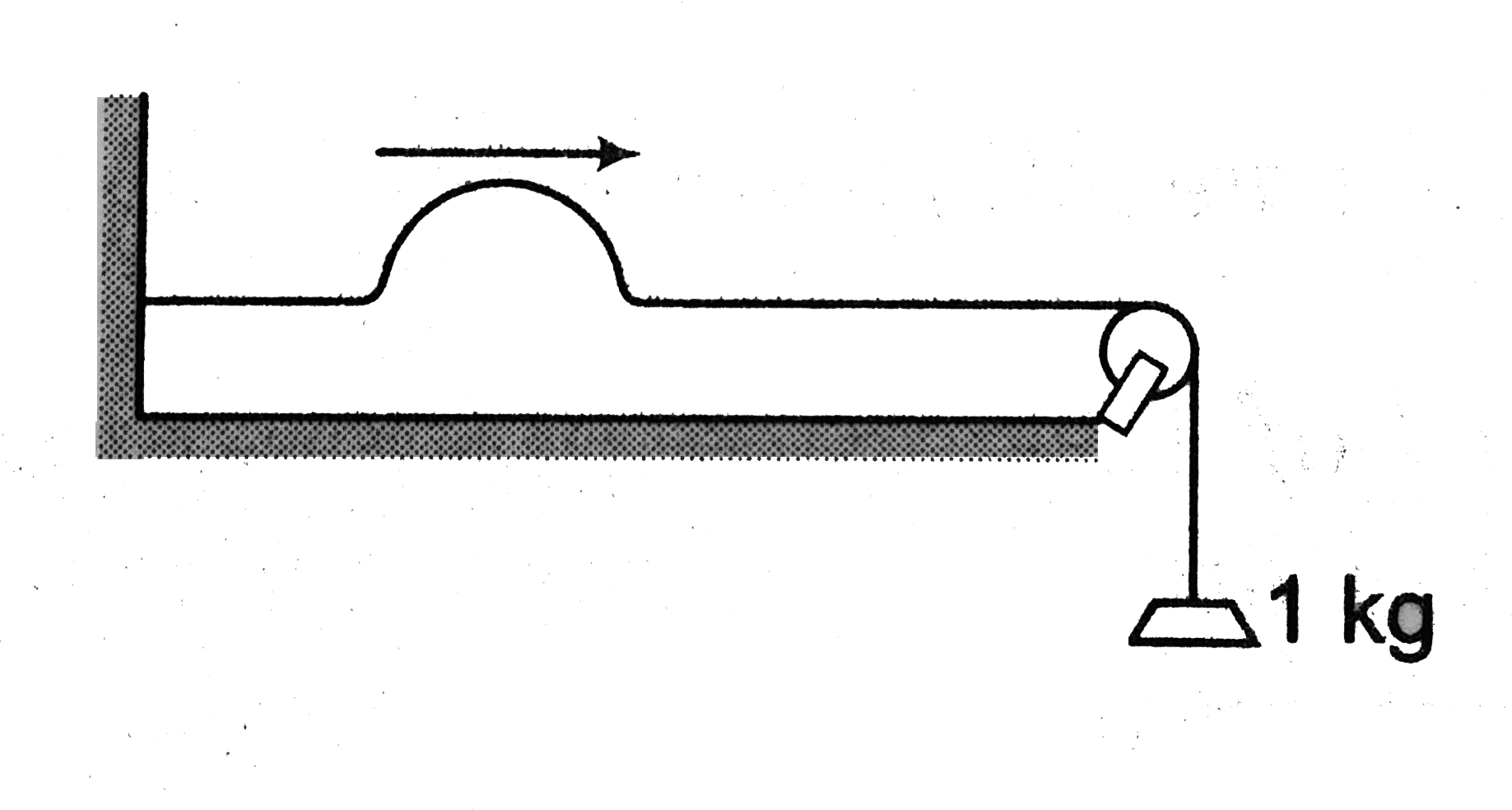 03:40View Solution
03:40View SolutionA wave pulse is generated at the bottom of a uniform string (of mass m and length l) Suspended from ceiling and supporting a block (of mass m) as shown.
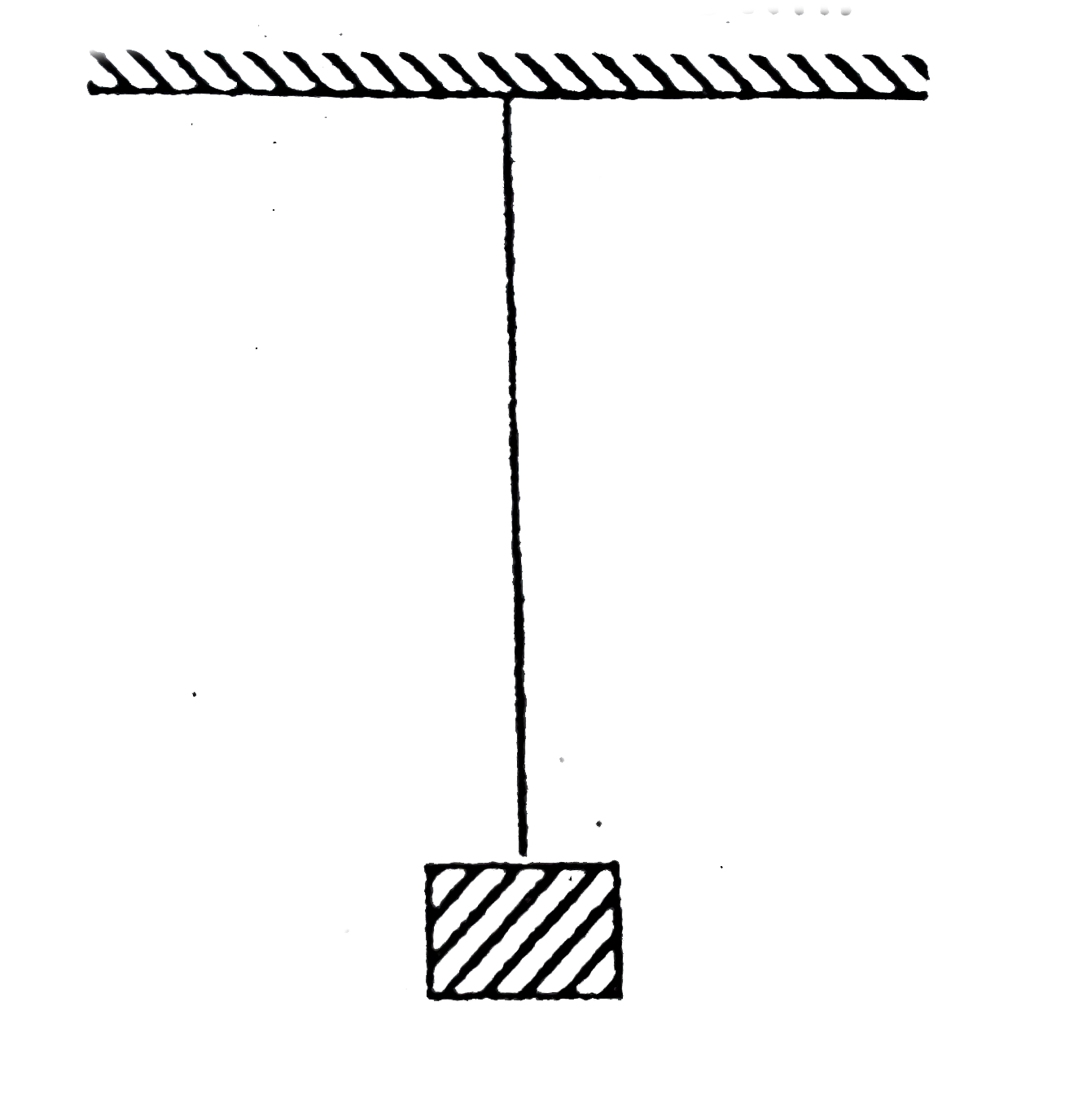 03:46View Solution
03:46View SolutionOne end of a string of length L is tied to the ceiling of a lift accelerating upwards with an acceleration 2. The other end o the string is freee. The linear mass density of the string varies linearly from 0 to λ from bottom to top. The acceleration of a wave pulled through out the string is pg4. Find p.
01:58View SolutionA mass of 2kg suspended by string of mass 6kg. A wave of wavelength 6 cm is produced at bottom of string. Wavelength of wave at top end of string will be
01:51View SolutionA rope of length L and mass m hangs freely from the ceiling. The velocity of transverse wave as a function of position x from the bottom is proportional to
03:33View SolutionFigure showa a string of linear mass density 1.0gcm−1onwhichawaveps–eistravell∈g.F∈dthetimetakenbytheps–e∈travell∈gthroughadistanceof50cmonthestr∈g.Takeg=10 ms^-2.
 03:44View Solution
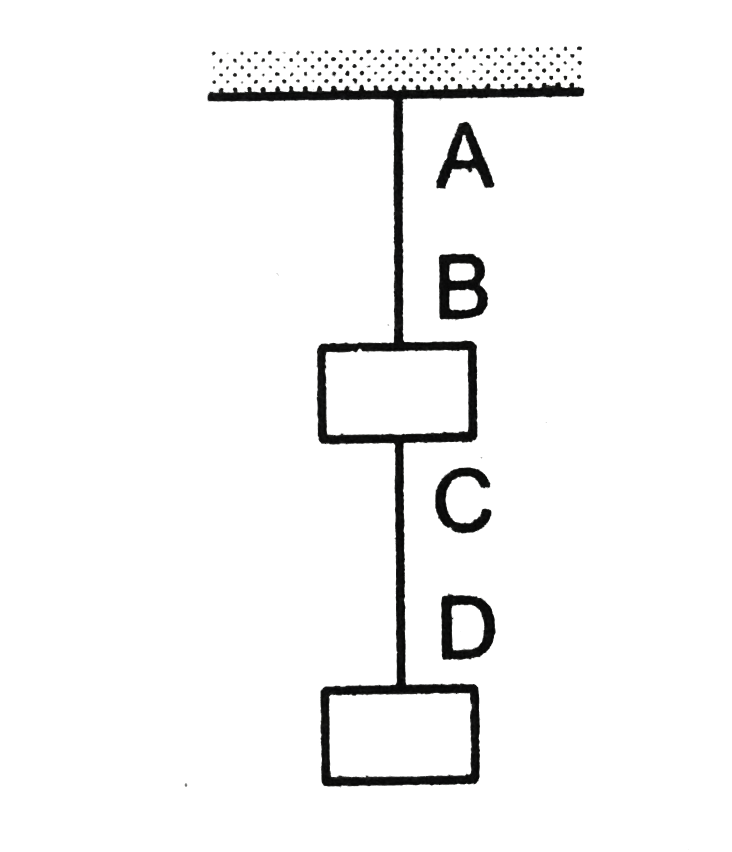
03:44View SolutionTwo blocks each having a mass of 3.2 kg are connected by a wire CD and the system is suspended from the ceiling by another wire AB . The linear mass density of the wire AB is 10 g /m and that of CD is 8gm−1. Find the speed of a transverse wave pulse produced in AB and in CD.
 03:10View Solution
03:10View SolutionA mass of 2kg suspended by string of mass 6kg. A wave of wavelength 6 cm is produced at bottom of string. Wavelength of wave at top end of string will be
View SolutionA 4 kg block is suspended from the ceiling of an elevator through a string having a linear mass density of 19.2 xx 10^(-3) kg m^(-1) . Find the speed with which a wave pulse can travel on the string if the elevator accelerates up at 2ms^(-2)(g=10 ms^(-2))
02:23View SolutionOne end of a string of length l is tied to the ceiling of a lift accelerating upwards with an acceleration g/2. The linear mass density of the string is μ(x)=μ0x1/2 where, x is measured from the bottom. The time taken by a pulse to reach from bottom to top is
03:06View SolutionFigure shows a string of linear mass density 1.0gcm−1 on which a wave pulse is travelling. Find the time taken by pulse in travelling through a distance of 50cm on the string. Take g=10ms−2
 09:11View Solution
09:11View SolutionA string is suspended from the ceiling. A wave train is produced at the bottom at regular interval. As the wave moves upwards
02:26View Solution

