A helium nucleus makes a full rotation in a circle of radius 0.8 metre in two seconds. The value of the magnetic field B at the centre of the circle will be
10−19μ0
10−19μ0
2×10−10μ0
2×10−10μ0
The correct Answer is:B
To find the magnetic field B at the center of the circle due to a helium nucleus making a full rotation, we can follow these steps:
Step 1: Identify the parameters
- Radius of the circle r=0.8 m
- Time for one full rotation T=2 s
- Charge of a helium nucleus q=2×1.6×10−19 C (since a helium nucleus has 2 protons)
Step 2: Calculate the current i
The current i can be calculated using the formula:
i=qT
Substituting the values:
q=2×1.6×10−19C=3.2×10−19C
i=3.2×10−19C2s=1.6×10−19A
Step 3: Use the formula for the magnetic field B
The magnetic field at the center of a circular loop carrying current is given by:
B=μ0i2r
Where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
Step 4: Substitute the values into the formula
Substituting the values of μ0, i, and r:
B=4π×10−7T m/A×1.6×10−19A2×0.8m
B=4π×10−7×1.6×10−191.6
B=4π×10−7×10−19T
B=4π×10−26T
Step 5: Calculate the numerical value
Using π≈3.14:
B≈4×3.14×10−26T≈12.56×10−26T
B≈1.256×10−25T
Final Answer
The value of the magnetic field B at the center of the circle is approximately 1.256×10−25T.
---
- Radius of the circle r=0.8 m
- Time for one full rotation T=2 s
- Charge of a helium nucleus q=2×1.6×10−19 C (since a helium nucleus has 2 protons)
The current i can be calculated using the formula:
i=qT
Substituting the values:
q=2×1.6×10−19C=3.2×10−19C
i=3.2×10−19C2s=1.6×10−19A
The magnetic field at the center of a circular loop carrying current is given by:
B=μ0i2r
Where μ0 (the permeability of free space) is approximately 4π×10−7T m/A.
Substituting the values of μ0, i, and r:
B=4π×10−7T m/A×1.6×10−19A2×0.8m
B=4π×10−7×1.6×10−191.6
B=4π×10−7×10−19T
B=4π×10−26T
Using π≈3.14:
B≈4×3.14×10−26T≈12.56×10−26T
B≈1.256×10−25T
The value of the magnetic field B at the center of the circle is approximately 1.256×10−25T.
Topper's Solved these Questions
Similar Questions
An electron makes (3×105) revolutions per second in a circle of radius 0.5 angstrom. Find the magnetic field B at the centre of the circle.
View SolutionA helium nucleus is moving in a circular path of radius 0.8m. If it takes 2s to complete one revolution. Find out magnetic field produced at the centre of the circle:
View Solution
Knowledge Check
A helium nucleus makes full rotation in a circle of radius 0.8 m in 2.5 seconds. The value of magnetic field B at the centre of the circle will be
A3.1π×10−26TB2π×10−26TC4π×10−25TD2π×10−25TA helium nucleus makes a full rotation in a circle of radius 0.8 m in 2 s. The value of the magnetic field B at the centre of the circle will be
A1019μ0B10−19μ0C2×10−10μ0D2×1010μ0A particle carrying a charge equal to 100 times the charge on an electron is rotating per second in a circular path of radius 0.8metre. The value of the magnetic field produced at the centre will be (μ0= permeability for vacuum)
A10−7μ0B10−17μ0C10−6μ0D10−7μ0
An alpha particle is completing one circular round of radius 0⋅8m in 2 seconds. Find the magnetic field at the centre of the circle. Electronic charge =1⋅6×1019C.
View SolutionThe magnetic field at the centre of dotted circle in the arrangement shown is
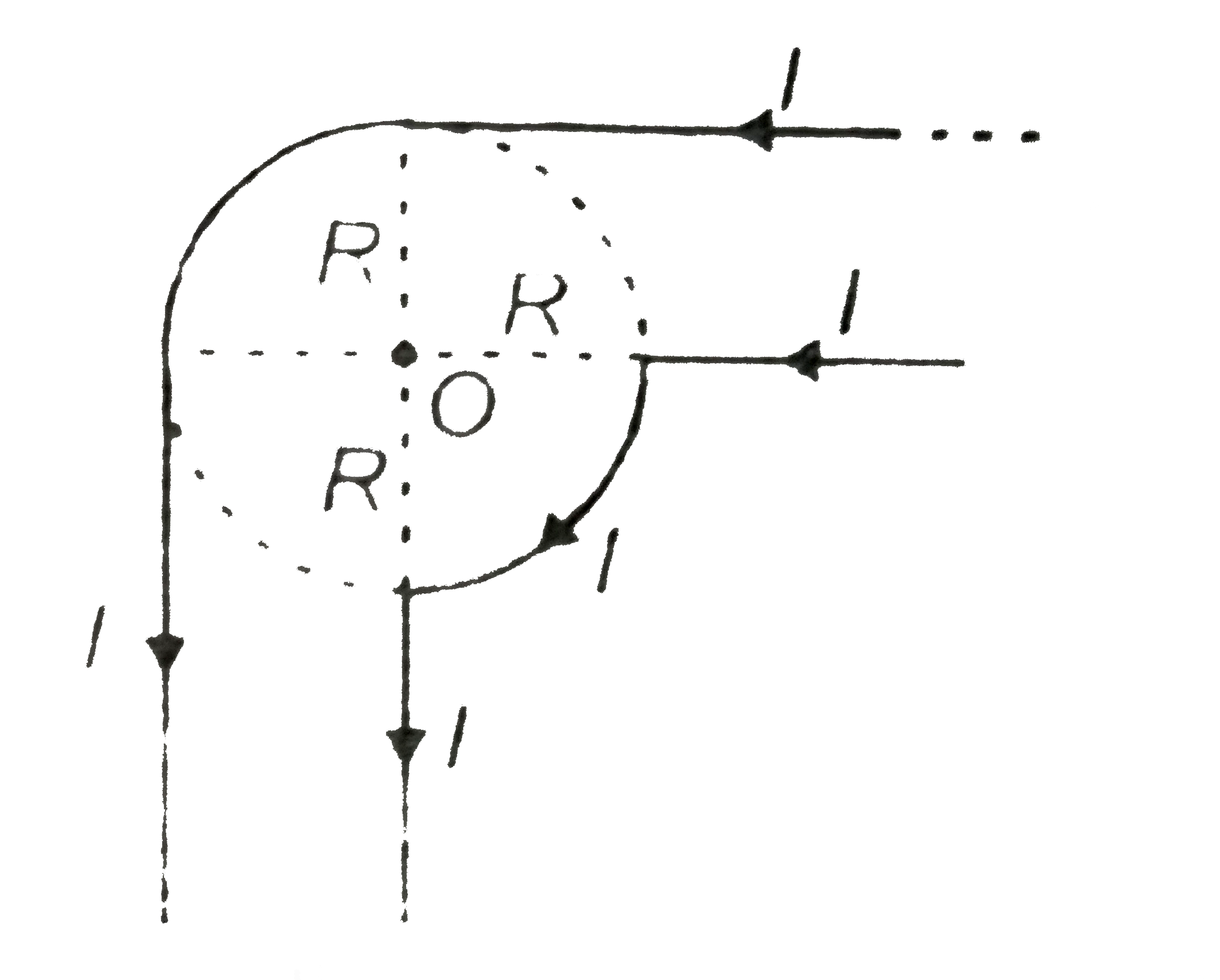
View SolutionA wire of length L carrying a current I is bent into a circle. The magnitude of the magnetic field at the centre of the circle is
View SolutionA charge 'e' moves round a circle of radius 'r' with a uniform speed 'v'. The magnitude of the magnetic induction at the centre of the circle is
View SolutionAn electron revolves in a circle of radius 0.4 A with a speed of 105 ms !. The magnitude of the magnetic field, produced at the centre of the circular path due to the motion of the electron, in weber metre 2 is
View Solution
