On connecting a battery to the two corners of a diagonal of a square conductor frame of side a the magnitude of the magnetic field at the centre will be
Zero
μ0πa
2μ0πa
4μ0iπa
The correct Answer is:A
To find the magnitude of the magnetic field at the center of a square conductor frame when connected to a battery at two corners of a diagonal, we can follow these steps:
1. Understand the Configuration:
- We have a square conductor frame with corners labeled A, B, C, and D. The battery is connected across the diagonal AC.
2. Current Distribution:
- When the battery is connected, current will flow through the sides AB, BC, CD, and DA. Since the sides are of equal length and made of the same material, the current will be equally divided among the two paths from A to C.
3. Calculate Current in Each Segment:
- Let the total current flowing from the battery be I. Since the current splits equally, the current in each segment (AB, BC, CD, DA) will be I/2.
4. Magnetic Field Due to Each Segment:
- The magnetic field at the center of the square due to a straight conductor carrying current can be calculated using the formula:
B=μ0I4πr
- Here, r is the distance from the wire to the point where the magnetic field is being calculated. For a square, the distance from the center to the midpoint of each side is a2√2.
5. Calculate Magnetic Field Contribution from Each Side:
- For each side of the square, the magnetic field at the center due to one side will be:
Bside=μ0(I/2)4π(a2√2)=μ0I√28πa
6. Direction of Magnetic Fields:
- The magnetic field produced by the current in opposite sides of the square will be in opposite directions. For example, if the current flows in a clockwise direction, the magnetic field due to sides AB and CD will point in one direction, while the magnetic field due to sides BC and DA will point in the opposite direction.
7. Net Magnetic Field Calculation:
- Since the magnetic fields from opposite sides cancel each other out, the net magnetic field at the center of the square will be:
Bnet=BAB+BCD+BBC+BDA=0
Final Answer:
The magnitude of the magnetic field at the center of the square conductor frame is 0.
- We have a square conductor frame with corners labeled A, B, C, and D. The battery is connected across the diagonal AC.
- When the battery is connected, current will flow through the sides AB, BC, CD, and DA. Since the sides are of equal length and made of the same material, the current will be equally divided among the two paths from A to C.
- Let the total current flowing from the battery be I. Since the current splits equally, the current in each segment (AB, BC, CD, DA) will be I/2.
- The magnetic field at the center of the square due to a straight conductor carrying current can be calculated using the formula:
B=μ0I4πr
- Here, r is the distance from the wire to the point where the magnetic field is being calculated. For a square, the distance from the center to the midpoint of each side is a2√2.
- For each side of the square, the magnetic field at the center due to one side will be:
Bside=μ0(I/2)4π(a2√2)=μ0I√28πa
- The magnetic field produced by the current in opposite sides of the square will be in opposite directions. For example, if the current flows in a clockwise direction, the magnetic field due to sides AB and CD will point in one direction, while the magnetic field due to sides BC and DA will point in the opposite direction.
- Since the magnetic fields from opposite sides cancel each other out, the net magnetic field at the center of the square will be:
Bnet=BAB+BCD+BBC+BDA=0
The magnitude of the magnetic field at the center of the square conductor frame is 0.
Topper's Solved these Questions
Similar Questions
A cell is connected across two points P and Q of a uniform circular conductor, figure. Prove that the magnetic field at its centre O will be zero.
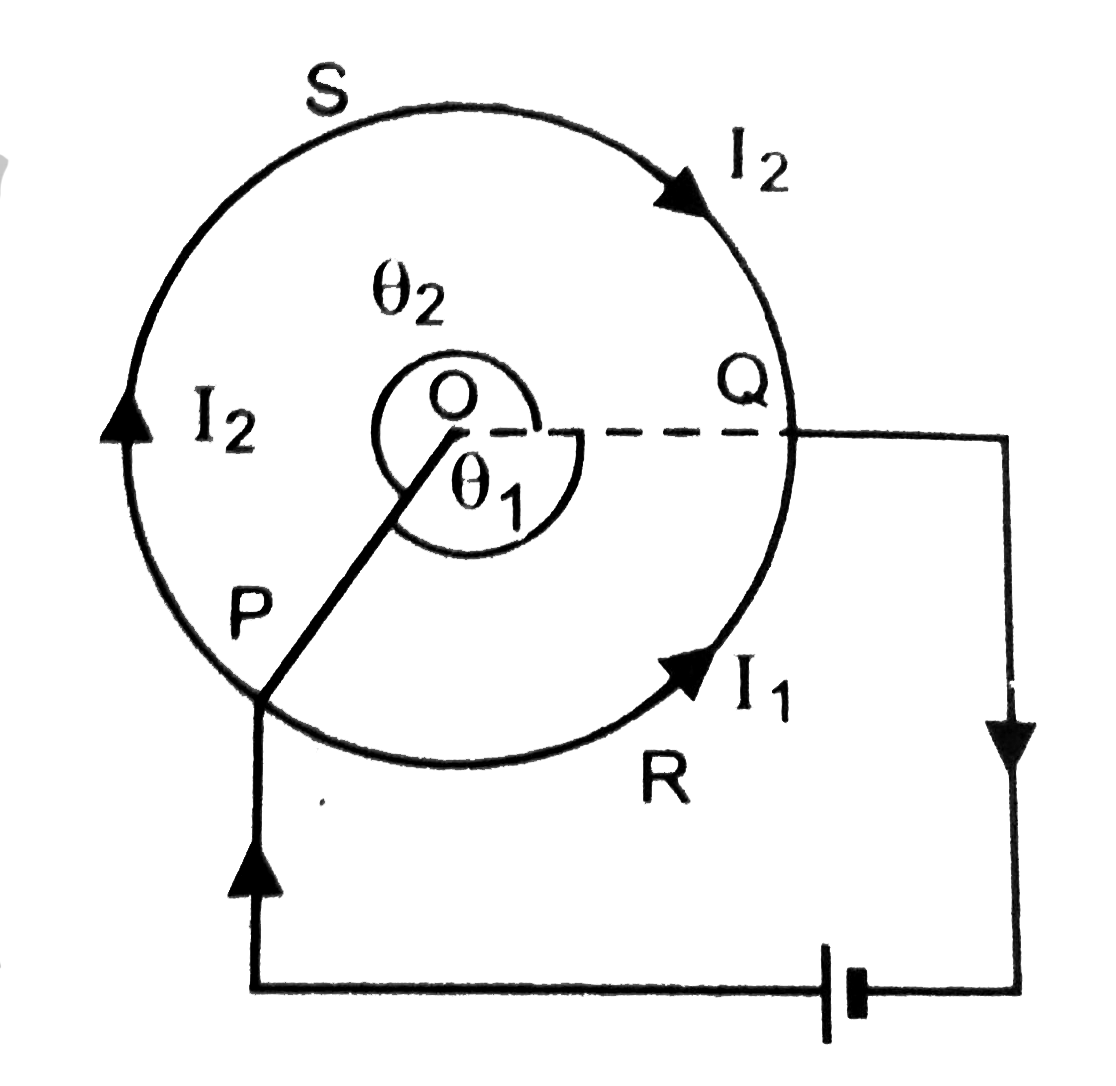 View Solution
View SolutionA square loop of side length L carries a current which produces a magnetic field B0 at the centre (O) of the loop. Now the square loop is folded into two parts with one half being perpendicular to the other (see fig). Calculate the magnitude of magnetic field at the centre O.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A square loop of side a carries a current I. The magnetic field at the center of the loop is
A2μ0I√2πaBμ0I√2πaC4μ0I√2πaDμ0Iπa - Question 2 - Select One
A square conducting loop of side length L carries a current I.The magnetic field at the centre of the loop is
Aindependent of LBproportional LCinversely proportional to LDlinearly proportional to L - Question 3 - Select One
The magnetic field at the centre of square of side a is
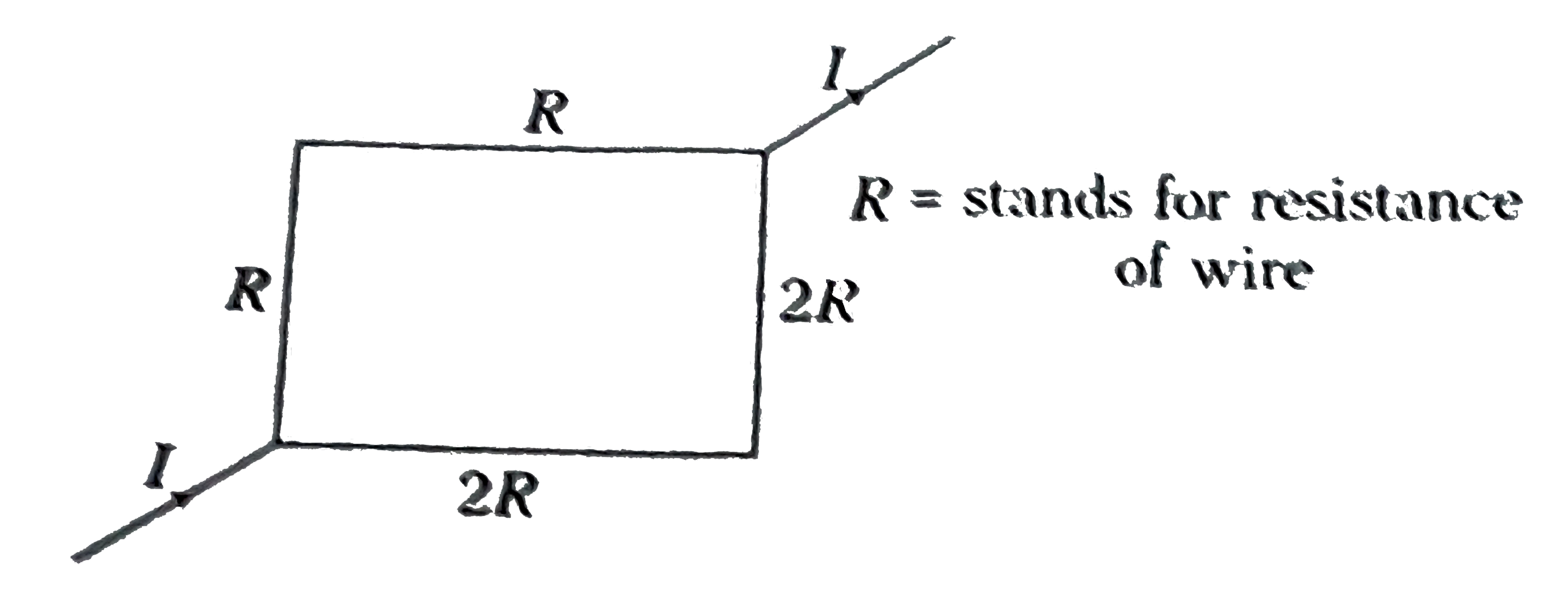 A√2μ0πaB√2μ0I3πaC23μ0IaDzero
A√2μ0πaB√2μ0I3πaC23μ0IaDzero
Two long straight conductors are connected radially to two arbitary points A and B of a circular conductor. Calculate the magnetic field at the center of the coil.
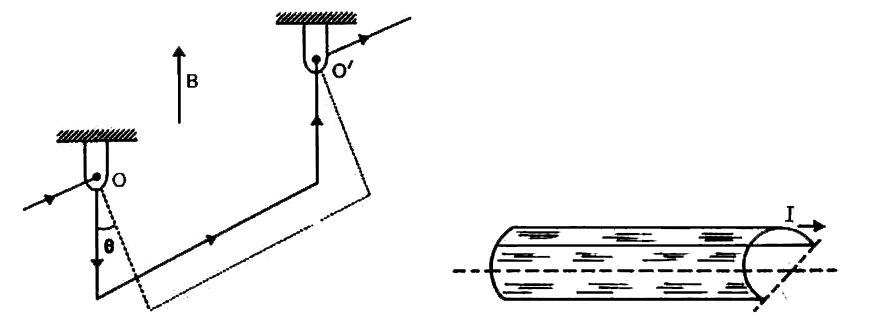 View Solution
View SolutionA current of 2A enters at the corner d of a square frame abcd of side 10cm and leaves at the opposite corner b.A magnetic field B=0.1T exists in the space in direction perpendicular to the plane of the frame as shown in figure.Find the magnitude and direction of the magnetic forces on the four sides of the frame.
 View Solution
View SolutionA circular conductor of uniform resistance per unit length, is connected to a battery of 4 V. The total resistance of the conductor is 4ω. The net magnetic field at the centre of the conductor is
 View Solution
View SolutionFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
View SolutionA cell is connected between two points of a uniformly thick circular conductor and i1andi2 are the currents flowing in two parts of the circular conductor of radius a The magnetic field at the centre of the loop will be
View Solution

