R=ρlA
What is ρ ?
ρ is a specific resistance of a substance.
Topper's Solved these Questions
- ELECTRIC CURRENTBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - ELECTRIC CURRENTEXERCISE - SECTION - IV (4 Marks Questions)
16 Videos
- ELECTRIC CURRENTBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - ELECTRIC CURRENTEXERCISE - EXPERIMENTATION AND FIELD INVESTIGATION
3 Videos
- CHEMICAL REACTIONS AND EQUATIONSBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - CHEMICAL REACTIONS AND EQUATIONSEXERCISE - ESSENTIAL MATERIAL FOR EXAMINATION PURPOSE
1 Videos
- ELECTROMAGNETISMBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - ELECTROMAGNETISMEXERCISE - CREATIVE QUESTION FOR NEW MODEL EXAMINATION (SEC-4)
30 Videos
Similar Questions
A non-homogenous sphere of radius R has the following density variation.
ρ=ρ0,r≤r/3,
ρ=ρ0/2,R3<r≤3R4,
ρ=ρ08,(3R)/(4)<r≤R,
What is the gravitational field due to sphere at distance 2R from center?
View SolutionThe resistance R of a wire is given by the relation R=ρlπr2. Percentage error in the measurement of ρ,landr is 1 % , 2% and 3% respectively. Then the percentage error in the measurement of R is
View Solution
Knowledge Check
A spherically symmetric gravitational system of particles has a mass densityρ={ρ0forr<R0forr>R whereρ0 is a constant. A test mass can undergo circular motion under the influence of the gravitational field of particles. Its speed v as a function of distahce r(0<r<OO) form the centre of the system is represented by
A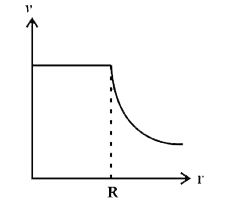 B
B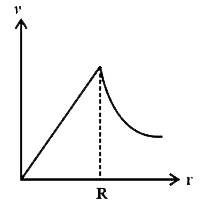 C
C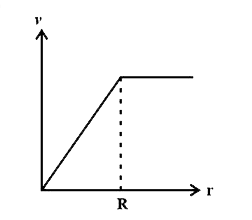 D
D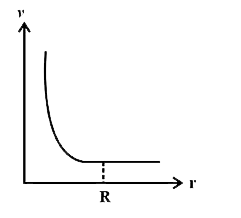
The resistance R of a wire is given by the relation R=ρlπr2. Percentage error in the measurement of ρ,landr is 1 % , 2% and 3% respectively. Then the percentage error in the measurement of R is
A6%B9%C8%D10%The density of the core a planet is ρ1 and that of the outer shell is ρ2. The radii of the core and that of the planet are R and 2R respectively. The acceleration due to gravity at the surface of the planet is same as at a depth R. Find the ratio of ρ1ρ2
 A2.3B4.5C3.2D5.4
A2.3B4.5C3.2D5.4
A solid sphere of radius R has a mass distributed in its volume of mass density ρ=ρ0 r, where ρ0 is constant and r is distance from centre. Then moment of inertia about its diameter is
View SolutionA non-conducting solid sphere has volume charge density that varies as ρ=ρ0 r, where ρ0 is a constant and r is distance from centre. Find out electric field intensities at following positions.
(i) r<R (ii) r≥R
View SolutionA non-conducting solid sphere has volume charge density that varies as ρ=ρ0 r, where ρ0 is a constant and r is distance from centre. Find out electric field intensities at following positions.
(i) r<R (ii) r≥R
View SolutionThe density of the core of planet is ρ1 and that of the outer shell is ρ2. The radius of the core that of the planet are R and 2R respectively. Gravitastional intensity at the surface of the planet is same as at a depth R. Find the ratio ρ1ρ2 , assuming them to be uniform independently.
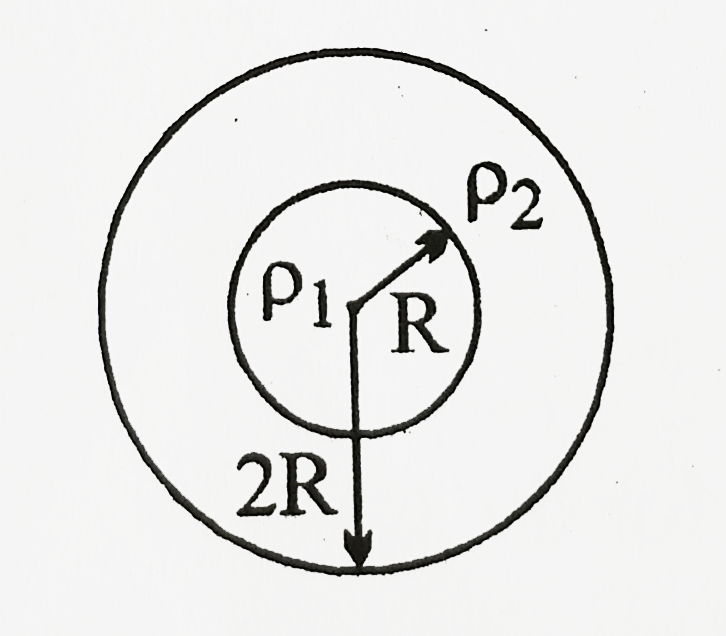
View SolutionThe earth may be regarded as a spherically shaped uniform core of density ρ1 and radius R2 surrounded by a uniform shell of thickness R2 and density ρ2. Find the ratio of ρ1ρ2 if the value of acceleration due to gravity is the same at surface as at depth R2 from the surface.
View Solution
