Two coherent monochromatic point sources $S_{1} and S_{2}$ of wavelength $λ = 600 n m$ are placed symmetrically on either side of the centre of the circle as shown. The sources are separated by a distance $d = 1.8 m m$ . This arrangement produces interference fringes visible as alternate bright and dark spots on the circumference of the circle. The angular separation between two consecutive bright spots is $Δ θ$ . Which of the following options is/are correct ?

A

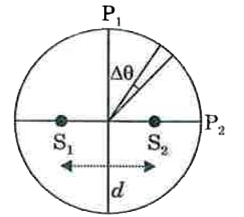
The total number of fringes produced between $P_{1} and P_{2}$ in the first quadrant is close to 3000

B

A dark spot will be formed at point $P_{2}$

C

At $P_{2}$ the order of the fringe will be maximum

D

The angular separation between two consecutive brigth spots decreases as we move from $P_{1}$ to $P_{2}$ along the first quadrant.

Text Solution

Verified by Experts

The correct Answer is:A, C

Path difference between the waves arriving at point $P_{1}$ from sources is zero because this point is equidistant from sources, hence there will be a bright at point $P_{1}$ . As we move from $P_{1}$ towards $P_{2}$ path difference increases and it becomes maximum at point $P_{2}$ . At the point $P_{2}$ this maximum possible path difference is equal to distance (1.8 mm) between the sources. Let this path difference at point $P_{2}$ in n times the wavelength $λ$ . We can write the following:
$n = \frac{d}{λ} = \frac{1.8 \times 10^{- 3}}{600 \times 10^{- 9}} = 3000$
We can see that option (a) is correct. Moreover path difference at point P is integral (n = 3000) multiple of wavelength, hence there will be bright at the point $P_{2}$ . Hence option (b) is not correct but option (c ) is correct.
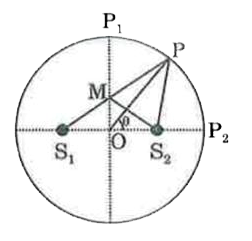
We shall now calculate path difference between waves arriving at point P from the two sources and for this calculation we shall assume that radius of the circle is much greater than the separation between sources. OP makes an angle $θ$ with the line joining sources. Since radius is very large, we can treat lines $S_{1} P, O P and S_{2} P$ almost parallel to each other. M is the foot of perpendicular drawn from $S_{2}$ on $S_{1} P$ .
Path difference $(x) = S_{2} P - S_{1} P \approx S_{1} M$
Angle $M S_{1} S_{2}$ is also approximately $θ$ , hence in triangle $M S_{1} S_{2}$ we can write the following:
$cos θ = \frac{S_{1} M}{S_{1} S_{2}}$
$\Rightarrow cos θ = \frac{x}{d} \Rightarrow x = d cos θ$
We can differentiate the above relation.
$\frac{d x}{d θ} = - d sin θ \Rightarrow \frac{Δ x}{Δ θ} = - d sin θ$
$\Rightarrow Δ x = - (d sin θ) Δ θ$
$Δ x$ is the difference prodced in the path difference as we move further by an angle $Δ θ$ . For consecutive fringes, difference in path difference must be $λ$ . Hence if we assume $Δ x$ equal to $λ$ , then $Δ θ$ will be the angular fringe width. Hence angular fringe width can be written as follows:
$\Rightarrow | Δ θ | = \frac{λ}{d sin θ}$
As we move from $P_{1}$ towards $P_{2}$ , value of $θ$ decreases from $90$ to $0$ , hence $sin θ$ decrease which means angular fringe width $Δ θ$ increases.

Updated on:21/07/2023

|

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two coherent point sources $S_{1} and S_{2}$ are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :

Astraigth lines
Bsemi-circle
Cconcentric circles
Dpoints
Two coherent point sources $S_{1}$ and $S_{2}$ are separated by a small distance $d$ as shown. The fringes obtained on the screen will be

Apoints
Bstraight lines
Csemi-circles
Dconcentric circles
Two coherent light sources $S_{1}$ and $S_{2} (λ = 6000 Å)$ are $1 m m$ apart from each other. The screen is placed at a distance of $25 c m$ from the sources. The width of the fringes on the screen should be
A(a) $0.015 c m$
B(b) $0.025 c m$
C(c) $0.010 c m$
D(d) $0.030 c m$

MODERN PUBLICATION-WAVE OPTICAL-OBJECTIVE TYPE QUESTIONS (C. MULTIPLE CHOICE QUESTIONS)

Home
Ask Doubt
Profile