A uniform non-conducting rod of mass m and length l has linear charge densities +λ and −λ on its two halves, as shown in the figure. It is hinged at its midpoint, so that it can rotate freely about the mid-point in a uniform electric field E parallel to X-axis. The rod is rotated by a small angle θ(<4∘) and released. Calculate the time period of small oscillations of the rod.
The torque due to the electrostatic force on a length dx of the rod at point A (about point O),
dτ1=x(dF1)sinθ=xλdxEsinθ
Similarly, torque due to the electrostatic force on a length dx of the rod at point B (about point O),
dτ2=x(dF2)sinθ=xλdxEsinθ

∴ Net torque on the rod,
τ=∫l20dτ1+∫l20dτ2
=2∫l20Eλdxxsinθ [dτ1=dτ2]
=2Eλθ=∫l20xdx [∵θ is small,sinθ≈θ]
∴τ=Eλl24θ ...(1)
In this case moment of intertia of rod,
I=ml212
∴τ=Iα=ml212α ...(2)
From equations (1) and (2) we get,
ml212α=Eλl2θ4or,α=3Eλmθ
∴ Time period of oscillations of the rod,
T=2π√θα=2π√m3Eλ
Topper's Solved these Questions
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - NCERT TEXTBOOK QUESTIONS WITH ANSWER HINT
24 Videos
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - NCERT EXEMPLAR QUESTIONS WITH ANSWER HINT
7 Videos
- ELECTRIC FIELDBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC FIELDEXERCISE - SECTION RELATION QUESTIONS
50 Videos
- ELECTRIC ENERGY AND POWERBOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC ENERGY AND POWEREXERCISE - CBSE SCANNER
7 Videos
- ELECTRIC POTENTIAL BOOK - CHHAYA PUBLICATIONCHAPTER - ELECTRIC POTENTIAL EXERCISE - CBSE Scanner
13 Videos
Similar Questions
A uniform nonconducting rod of mass ma and length l, with charge density λ as shown in fig. is hanged at the midpoint at origin so that it can rotate in a horizontal plane without any friction. A uniform electric field E exists parallel to x axis in the entire region. Calculated the period of small oscillation of the rod .

View SolutionA uniform nonconducting rod of mass ma and length l, with charge density λ as shown in fig. is hanged at the midpoint at orgin so that it can rotate in a horizontal plane without any friction. A uniform electric field E exists paralled to xaxis in th entire region. Calculated the period of small oscillation of the rod .

View Solution
Knowledge Check
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
 A2π√lgB2π√2lgC2π√2l3gD2π√l3g
A2π√lgB2π√2lgC2π√2l3gD2π√l3gConsider the situation shown in the figure. Uniform rod of length L can rotat freely about the hinge A in vertical plane. Pulleys and stringa are light and frictionless. If the rod remains horizontal at rest when the system is released then the mass of the rod is
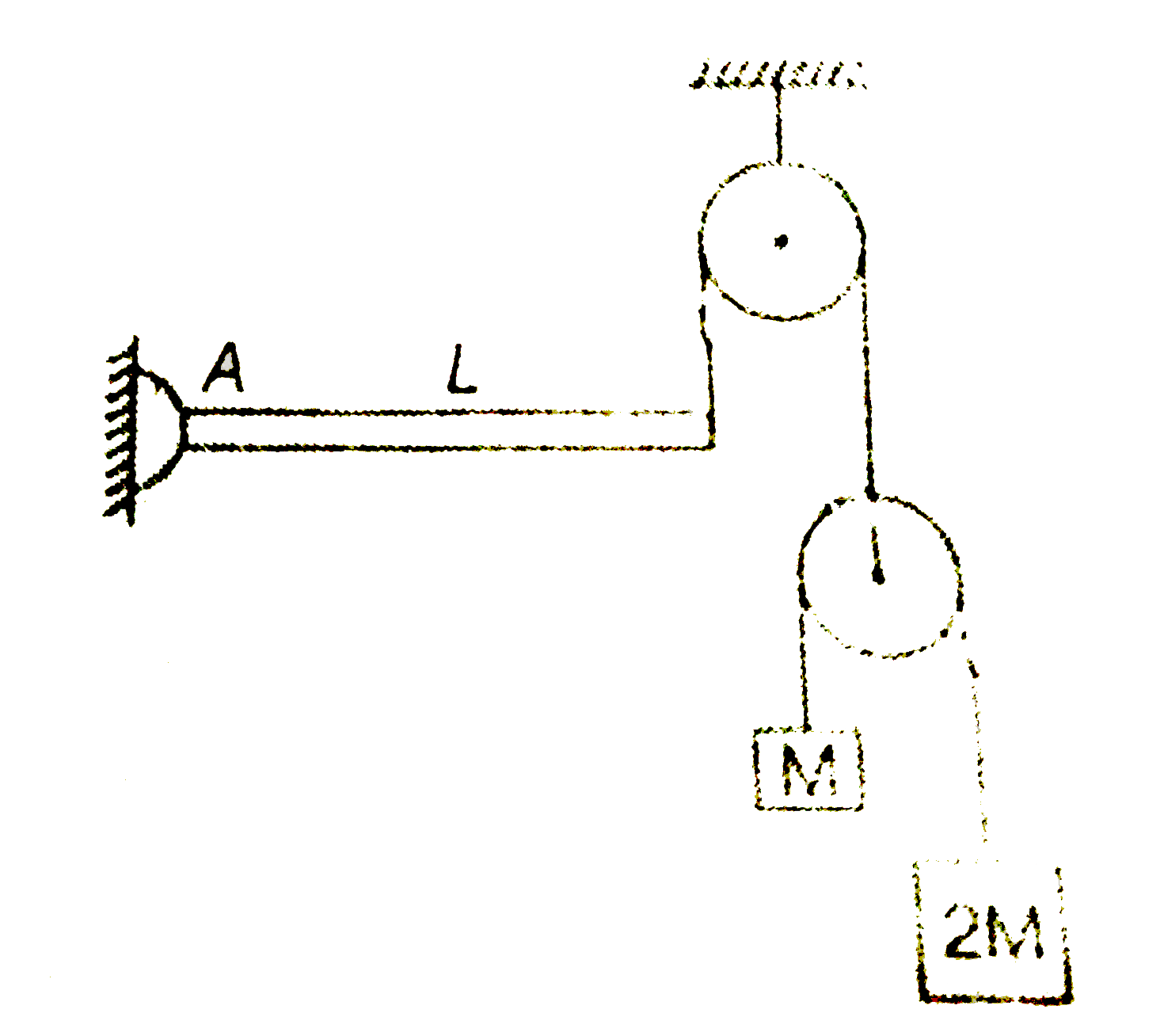 A43MB83MC163MD323M
A43MB83MC163MD323MA large sheet carries uniform surface charge density σ . A rod of length 2l has a linear charge density lamba on one half and −λ on the second half. The rod is hinged at the midpoint O and makes an angle θ with the normal to the sheet. The torque experience by the rod is
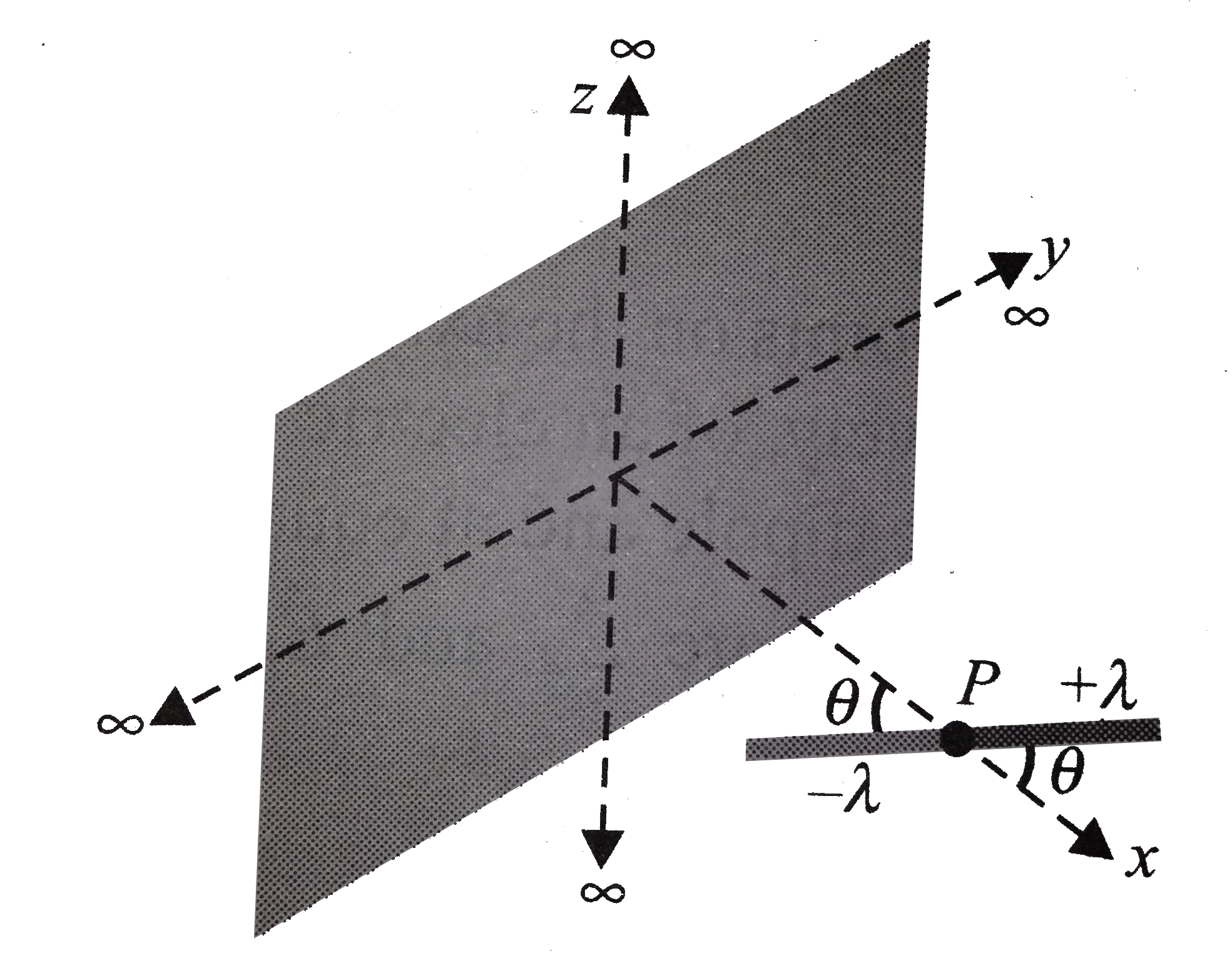 A0Bσλl22ε0sinθCσλl2ε0sinθDσλl2ε0
A0Bσλl22ε0sinθCσλl2ε0sinθDσλl2ε0
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View SolutionConsider the situation shown in the figure. Uniform rod of length L can rotat freely about the hinge A in vertical plane. Pulleys and stringa are light and frictionless. If the rod remains horizontal at rest when the system is released then the mass of the rod is

View SolutionA uniform rod of mass m and length L is fixed to an axis, making an angle θ with it as shown in the figure. The rod is rotated about this axis so that the free end of the rod moves with a uniform speed ‘v’. Find the angular momentum of the rod about the axis. Is the angular momentum of the rod about point A constant?

View SolutionA large sheet carries uniform surface charge density σ . A rod of length 2l has a linear charge density λ on one half and −λ on the second half. The rod is hinged at the midpoint O and makes an angle θ with the normal to the sheet. The torque experience by the rod is

View SolutionA uniform rod of mass m and length l makes a constant angle θ with an axis of rotation which passes through one end of the rod. Its moment of inertia about this axis is
View Solution
