A particle of mass m is attached to one end of missless rigid non-conducting rod of length $l$ . Another particle of the same mass is attached to the other end of the rod. Two particles carry charges +q and -q . This arrangement is held in the region of uniform electric field E such that the rod makes and angle $θ (< 5^{\circ})$ with the field direction. Find an expression for the minimum time that is needed for the rod to become parallel to the field after it is set free.

Text Solution

Verified by Experts

As the rod has two charges of equal magnitude (be opposite in nature), the torque acting on the rod,
$τ = q E \times l sin θ$
or, $τ = q E l θ [∵ θ < 5^{\circ}]$
We know, $τ = I α$
[where I = moment of inertia and $α$ = angular acceleration]

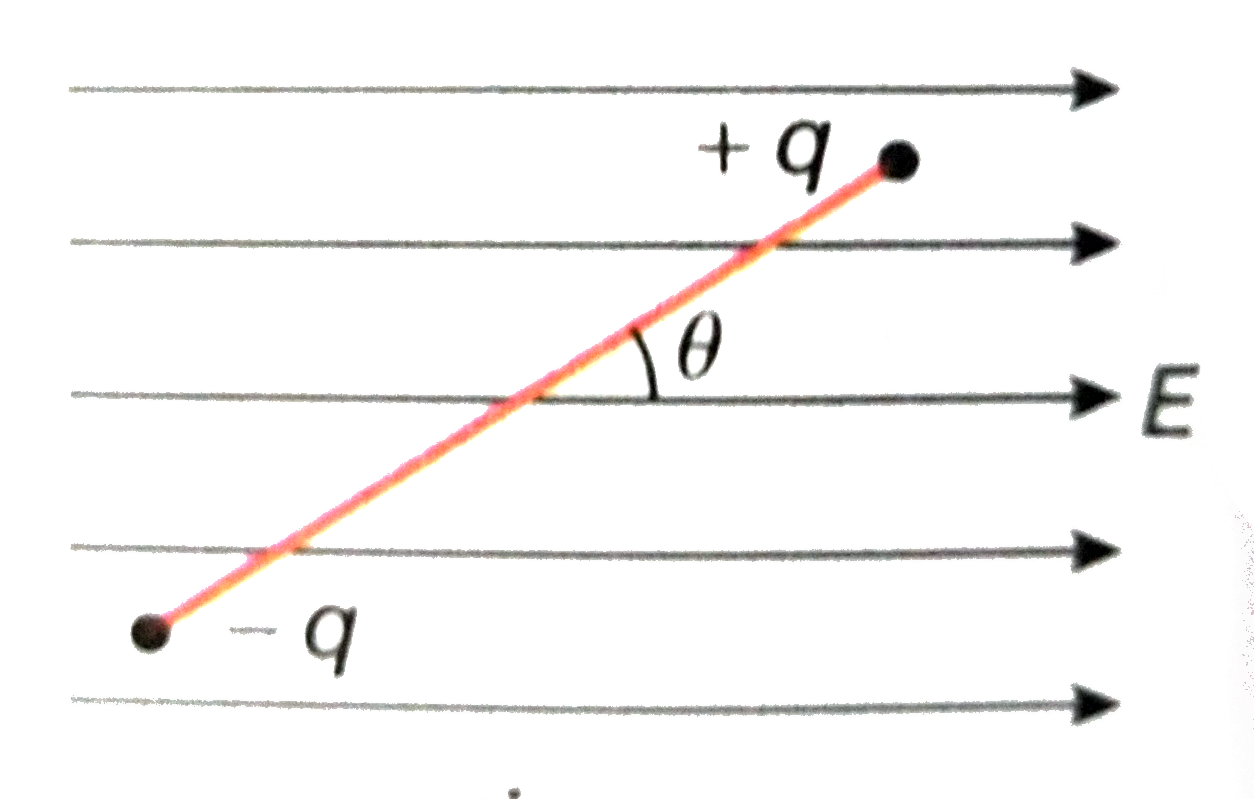
Hence, $I α = q E l θ or, α = \frac{q E l θ}{I}$
$∴$ Time period, $T = 2 π \sqrt{\frac{angular displacement}{angular acceleration}} = 2 π \sqrt{\frac{I}{q E l}}$
Now, moment of inertia of the dipole,
$I = [{(\frac{l}{2})}^{2} + {(\frac{l}{2})}^{2}] m = \frac{1}{2} m l^{2}$
$∴ T = 2 π \sqrt{\frac{m l^{2}}{2 q E l}} = 2 π \sqrt{\frac{m l}{2 q E}}$
$∴$ Required time, $t = \frac{1}{4} \times time period = \frac{T}{4} = \frac{π}{2} \sqrt{\frac{m l}{2 q E}}$

Updated on:21/07/2023