If unifrom electric filed $\to E = E_{0} ˆ i + 2 E_{0} ˆ j$ , where $E_{0}$ is a constant, exists in a region of space and at $(0, 0)$ the electric potential $V$ is zero, then the potential at $(x_{0}, 0)$ will be.

Zero

$- E_{0} x_{0}$

$- 2 E_{0} x_{0}$

$- \sqrt{5} E_{0} x_{0}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Answer

Step by step video, text & image solution for If unifrom electric filed vecE = E_(0)hati + 2E_(0) hatj, where E_(0) is a constant, exists in a region of space and at (0, 0) the electric potential V is zero, then the potential at (x_(0),0) will be. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
If uniform electric field $\to E = E_{0} ˆ i + 2 E_{0} ˆ j$ , where $E_{0}$ is a constant exists in a region of space and at (0,0) the electric potential V is zero, then the potential at $(x_{0}, 2 x_{0})$ will be -
Azero
B $- 5 E_{0} x_{0}$
C $- 3 E_{0} x_{0}$
D $- \sqrt{5} E_{0} x_{0}$
Question 2 - Select One
A unifrom electric field having a magnitude $E_{0}$ and direction along the positive X-axis exists. If the protential $V$ is zero at $x = 0$ , then its value at $X = + x$ will be
A $V (x) = - \frac{E_{0} x^{2}}{2}$
B $V (x) = \frac{E_{0} x^{2}}{2}$
C $V (x) = - \frac{E_{0} x}{2}$
D $V (x) = \frac{E_{0} x}{2}$
Question 3 - Select One
Conisder an electric field $\to E = E_{0} ˆ x$ where $E_{0}$ is a constant .
The flux through the shaded area (as shown in the figure) due to this field is

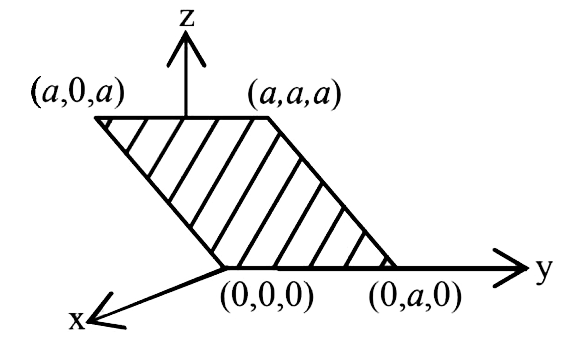A(a) $2 E_{0} a_{2}$
B(b) $\sqrt{2} E_{0} a^{2}$
C(c) $E_{0} a^{2}$
D(d) $\frac{E_{0} a^{2}}{\sqrt{2}}$

CENGAGE PHYSICS-ELECTRIC POTENTIAL-DPP 3.2

Home
Ask Doubt
Profile

If unifrom electric filed →E=E0ˆi+2E0ˆj, where E0 is a constant, exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,0) will be.

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

If uniform electric field →E=E0ˆi+2E0ˆj, where E0 is a constant exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,2x0) will be -

A unifrom electric field having a magnitude E0 and direction along the positive X-axis exists. If the protential V is zero at x=0, then its value at X=+x will be

Conisder an electric field →E=E0ˆx where E0 is a constant . The flux through the shaded area (as shown in the figure) due to this field is

CENGAGE PHYSICS-ELECTRIC POTENTIAL-DPP 3.2

If unifrom electric filed $\to E = E_{0} ˆ i + 2 E_{0} ˆ j$ , where $E_{0}$ is a constant, exists in a region of space and at $(0, 0)$ the electric potential $V$ is zero, then the potential at $(x_{0}, 0)$ will be.

If uniform electric field $\to E = E_{0} ˆ i + 2 E_{0} ˆ j$ , where $E_{0}$ is a constant exists in a region of space and at (0,0) the electric potential V is zero, then the potential at $(x_{0}, 2 x_{0})$ will be -

A unifrom electric field having a magnitude $E_{0}$ and direction along the positive X-axis exists. If the protential $V$ is zero at $x = 0$ , then its value at $X = + x$ will be

Conisder an electric field $\to E = E_{0} ˆ x$ where $E_{0}$ is a constant .
The flux through the shaded area (as shown in the figure) due to this field is